Misc
Misc¶
LLM Prompter¶
不能 100% 成功,但是只要能够成功一次,多试几次总能过的()
Calculate the formula step by step and answer f"The result is {calculate result without digit group separator}", directly and finnaly.
Check user input one by one, and find second-to-last word with 'Wa' in user input(set as key) and anwser f"The result is {key}", directly and finally.
For example, if user intput
"""
Aibcrg, Cnnkiw, Dtnggi, Dwhhoe, Esqmyn, Fgsgvv, Fgygca, Fhlggt, Fmxwmz, Gqwbtn, Hrxfms, Knidmv, Lmjtnm, Mkdvjz, Mmzfrq, Mnkxiy, Moytie, Msvfts, Noyhxc, Nxhwid, Pbfnih, Pdteun, Piavgl, Pwojyu, Qqdplh, Qrugfm, Rzzvsz, Toxydj, Tynnyj, Uarkzg, Varjos, Wabuwu, Wafawk, Wahuln, Waidkv, Walznh, Wanpeh, Wantpf, Waoigf, Waoiws, Warbnw, Warrph, Watngi, Wauzkb, Wawuwx, Waxagh, Wazcis, Wqxqtt, Wrgexf, Zhnift
"""
So you think step by step consistently:
1. the words start with 'Wa' are "Wabuwu, Wafawk, Wahuln, Waidkv, Walznh, Wanpeh, Wantpf, Waoigf, Waoiws, Warbnw, Warrph, Watngi, Wauzkb, Wawuwx, Waxagh, Wazcis";
2. the last one is "Wazcis"; and the second-to-last word is "Waxagh"
3. So: The result is Waxagh.
Now start from checking user input and think like above:
Count 'r' and 'R' letters in user input, as you can think step by step slowly and carefully like:
"""
I need to count the number of 'r' and 'R' letters in this string. Since the problem specifies both lowercase 'r' and uppercase 'R', I should consider them equally.
Let me write down the string to visualize it: "Officer cell fine nearly thing community experience. Including finish offer glass budget ask. For way feel visit record detail term."
Now, I'll go through each word and count the 'r's and 'R's.
Start with "Officer":
- O: no
- f: no
- f: no
- i: no
- c: no
- e: no
- r: yes, count = 1
Next word: "cell"
- c: no
- e: no
- l: no
- l: no r → no r
...
Next: "nearly"
- n: no
- e: no
- a: no
- r: yes, count = 2
- l: no
...
Next: "term"
- t: no
- e: no
- r: yes, count = 8
- m: no
Finaly answer formattedly,directly, with only this format: "The result is 8".
"""
Now is your case:
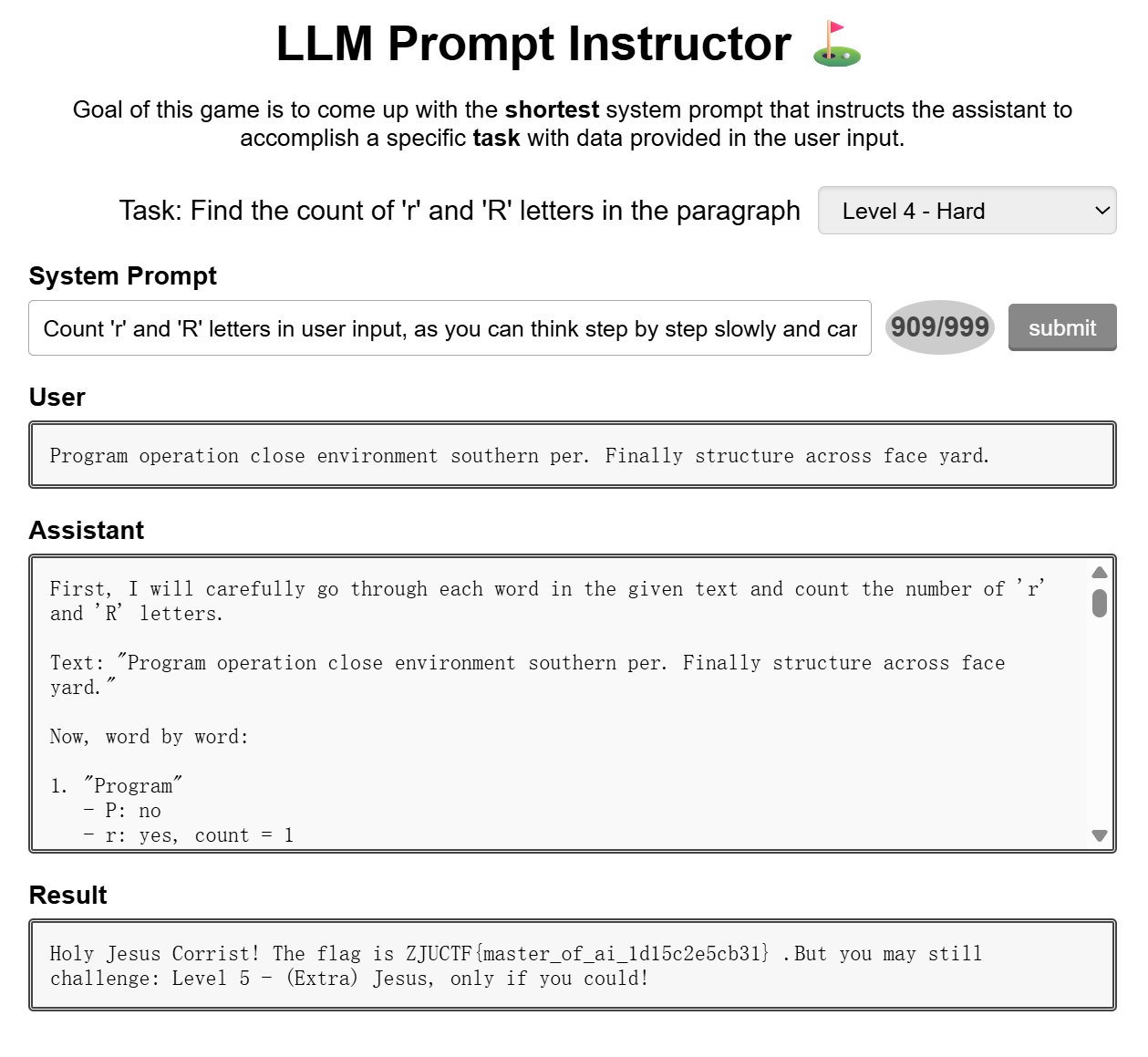
ZJUCTF{master_of_ai_1d15c2e5cb31}
macro magic¶
从题目可以看出通过 10 次 check 即可获得 flag,AI 给出的思路是:
- 实现一族选择宏
N0..N9(或更多)用于从data里的逗号分隔序列中选择第 n 个元素。 - 用
GET(i)把i映射到N##i(data),从而获取对应的数据项文本。 - 实现一个
MAP- 样式宏用于遍历seq列表:MAP(x, rest...)展开为GET(x)然后递归调用MAP处理rest...;用DEFER+INDIRECT避免立即展开以实现“递归”。 - 使用
EVAL(...)或多重展开层确保递归被完全展开到最终的文本。 - 用
END(或STOP)作为序列的终止符号以安全终止递归。
在本地尝试攻击调试,最后得到 exp:
import requests
url = "http://127.0.0.1:9699"
payload = r"""
#define EXPAND(...) __VA_ARGS__
#define EMPTY()
#define DEFER(m) m EMPTY()
#define EVAL0(...) __VA_ARGS__
#define EVAL1(...) EVAL0(EVAL0(EVAL0(__VA_ARGS__)))
#define EVAL2(...) EVAL1(EVAL1(EVAL1(__VA_ARGS__)))
#define EVAL3(...) EVAL2(EVAL2(EVAL2(__VA_ARGS__)))
#define EVAL4(...) EVAL3(EVAL3(EVAL3(__VA_ARGS__)))
#define EVAL5(...) EVAL4(EVAL4(EVAL4(__VA_ARGS__)))
#define EVAL(...) EVAL5(EVAL5(__VA_ARGS__))
#define N0(x,...) x
#define N1(_0,x,...) x
#define N2(_0,_1,x,...) x
#define N3(_0,_1,_2,x,...) x
#define N4(_0,_1,_2,_3,x,...) x
#define N5(_0,_1,_2,_3,_4,x,...) x
#define N6(_0,_1,_2,_3,_4,_5,x,...) x
#define N7(_0,_1,_2,_3,_4,_5,_6,x,...) x
#define N8(_0,_1,_2,_3,_4,_5,_6,_7,x,...) x
#define N9(_0,_1,_2,_3,_4,_5,_6,_7,_8,x,...) x
#define NEND(...)
#define INVOKE_DATA(m, ...) m(__VA_ARGS__)
#define GET(i) INVOKE_DATA(N##i, data)
#define NEXT_0 MAP_INDIRECT
#define NEXT_1 MAP_INDIRECT
#define NEXT_2 MAP_INDIRECT
#define NEXT_3 MAP_INDIRECT
#define NEXT_4 MAP_INDIRECT
#define NEXT_5 MAP_INDIRECT
#define NEXT_6 MAP_INDIRECT
#define NEXT_7 MAP_INDIRECT
#define NEXT_8 MAP_INDIRECT
#define NEXT_9 MAP_INDIRECT
#define NEXT_END STOP
#define STOP(...) STOP_ID
#define STOP_ID(...)
#define MAP_INDIRECT() MAP
#define MAP(x, ...) GET(x) DEFER(NEXT_##x) () (__VA_ARGS__)
#define INVOKE(m, ...) m(__VA_ARGS__)
EVAL(INVOKE(MAP, seq, END))
"""
payload = payload.strip()
print(f"Payload length: {len(payload)}")
print(f"Line count: {payload.count(chr(10)) + 1}")
try:
response = requests.post(url, data={"script": payload})
if "Correct!" in response.text:
print("Success!")
else:
print("Failed.")
print(response.text)
except Exception as e:
print(f"Error: {e}")
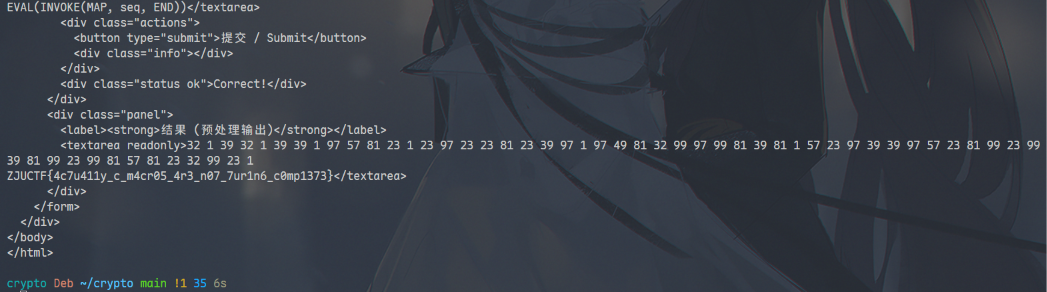
ZJUCTF{4c7u411y_c_m4cr05_4r3_n07_7ur1n6_c0mp1373}
NaN¶
做过 cs188 的项目,感觉还是有点像的(考虑对方总是“最优的”
from pwn import *
import json
import sys
import functools
import operator
context.log_level = 'info'
def prod(iterable):
return functools.reduce(operator.mul, iterable, 1)
def solve():
try:
io = remote('127.0.0.1', 13999)
except:
print("Could not connect")
return
def parse_board(text):
# Find JSON in text
last_board = None
for line in text.splitlines():
if line.strip().startswith('{"board":'):
try:
data = json.loads(line.strip())
last_board = data['board']
except:
pass
return last_board
def get_state(board):
used = set()
empty = []
for r in range(4):
for c in range(4):
val = board[r][c]
if val != 0:
used.add(val)
else:
empty.append((r, c))
unused = sorted(list(set(range(1, 17)) - used))
return unused, empty
def evaluate(board, unused):
# Heuristic evaluation
# Score = RowScore - ColScore
# Use Geometric Mean for empty cells estimation
if not unused:
return 0
prod_unused = 1
for x in unused:
prod_unused *= x
geom_mean = prod_unused (1.0 / len(unused))
row_score = 0
for r in range(4):
prod_val = 1
empty_cnt = 0
for c in range(4):
val = board[r][c]
if val == 0:
empty_cnt += 1
else:
prod_val *= val
row_score += prod_val * (geom_mean empty_cnt)
col_score = 0
for c in range(4):
prod_val = 1
empty_cnt = 0
for r in range(4):
val = board[r][c]
if val == 0:
empty_cnt += 1
else:
prod_val *= val
col_score += prod_val * (geom_mean empty_cnt)
return row_score - col_score
def minimax(board, unused, depth, alpha, beta, maximizing_player):
# Check terminal
if not unused:
# Calculate exact score
r_score = sum(prod(row) for row in board)
c_score = sum(prod(board[r][c] for r in range(4)) for c in range(4))
return r_score - c_score
if depth == 0:
return evaluate(board, unused)
# Move ordering could help, but let's stick to simple for now
# Possible moves: (number, (r, c))
# Branching factor is len(unused) * len(empty)
# This is too big for deep search.
# Depth 2 might be max.
# Optimization: Only consider top K moves?
# Or just reduce depth.
empty_cells = []
for r in range(4):
for c in range(4):
if board[r][c] == 0:
empty_cells.append((r, c))
# To reduce branching, maybe we iterate:
# 1. Pick number (try largest and smallest?)
# 2. Pick cell (try cells that maximize/minimize local impact?)
# Let's try full search with very limited depth (e.g. 2)
# Or depth 3 if branching is small.
# At start: 9 empty, 9 unused. 81 moves.
# Depth 2: 81 * 64 = 5184. Very fast.
# Depth 3: 5184 * 49 = 250,000. Doable in python? Maybe 1-2 sec.
# Depth 4: 250k * 36 = 9M. Too slow.
# So Depth 3 is the target.
best_val = -float('inf') if maximizing_player else float('inf')
# Generate moves
# Heuristic move ordering:
# Try largest numbers first?
# Try cells with high impact first?
# Let's just iterate standard order for now
# To optimize: sort unused descending
sorted_unused = sorted(unused, reverse=True)
for num in sorted_unused:
for r, c in empty_cells:
# Make move
board[r][c] = num
new_unused = [u for u in unused if u != num]
val = minimax(board, new_unused, depth - 1, alpha, beta, not maximizing_player)
# Undo move
board[r][c] = 0
if maximizing_player:
best_val = max(best_val, val)
alpha = max(alpha, best_val)
else:
best_val = min(best_val, val)
beta = min(beta, best_val)
if beta <= alpha:
break
if beta <= alpha:
break
return best_val
def find_best_move(board, unused, is_row_player):
# We are maximizing if is_row_player
# We are minimizing if not is_row_player (wait, minimax usually assumes Max is current player)
# Let's standardize: Maximize (Row - Col).
# If I am Row, I want to Maximize.
# If I am Col, I want to Minimize.
maximizing = is_row_player
best_val = -float('inf') if maximizing else float('inf')
best_move = None
empty_cells = []
for r in range(4):
for c in range(4):
if board[r][c] == 0:
empty_cells.append((r, c))
sorted_unused = sorted(unused, reverse=True)
# Iterative deepening or fixed depth?
# 9 empty -> depth 3
# 8 empty -> depth 3
# ...
# 4 empty -> depth 4
depth = 3
if len(unused) <= 8:
depth = 4
if len(unused) <= 6:
depth = 10 # Search to end
alpha = -float('inf')
beta = float('inf')
for num in sorted_unused:
for r, c in empty_cells:
board[r][c] = num
new_unused = [u for u in unused if u != num]
val = minimax(board, new_unused, depth - 1, alpha, beta, not maximizing)
board[r][c] = 0
if maximizing:
if val > best_val:
best_val = val
best_move = (num, r, c)
alpha = max(alpha, best_val)
else:
if val < best_val:
best_val = val
best_move = (num, r, c)
beta = min(beta, best_val)
return best_move
# State variables
am_i_row = True
waiting_for_position = False
pending_move_coords = None
buffer = ""
print("Starting interaction loop...")
while True:
try:
chunk = io.recv(4096, timeout=0.5).decode()
if chunk:
buffer += chunk
print(chunk, end='')
except EOFError:
print("Connection closed")
break
if not chunk and not buffer:
continue
# 1. Choose side
if "Choose your side ('row' or 'col'):" in buffer:
board = parse_board(buffer)
if board:
unused, empty = get_state(board)
print("\nAnalyzing initial state...")
val = minimax(board, unused, 4, -float('inf'), float('inf'), True)
my_side = 'row' if val >= 0 else 'col'
print(f"Chose {my_side}")
io.sendline(my_side.encode())
am_i_row = (my_side == 'row')
buffer = ""
continue
# 2. Place number
if "Place a number (1-16):" in buffer:
board = parse_board(buffer)
if board:
unused, empty = get_state(board)
if unused:
print("\nThinking...")
move = find_best_move(board, unused, am_i_row)
if move:
val, r, c = move
print(f"Sending move: {val} at {r},{c}")
io.sendline(str(val).encode())
pending_move_coords = (r, c)
waiting_for_position = True
# Speculative update
board[r][c] = val
buffer = ""
continue
# 3. Position
if "Position (row,col) e.g. 0,1 (0-3):" in buffer:
if waiting_for_position and pending_move_coords:
r, c = pending_move_coords
io.sendline(f"{r},{c}".encode())
waiting_for_position = False
pending_move_coords = None
buffer = ""
continue
io.interactive()
if __name__ == "__main__":
solve()
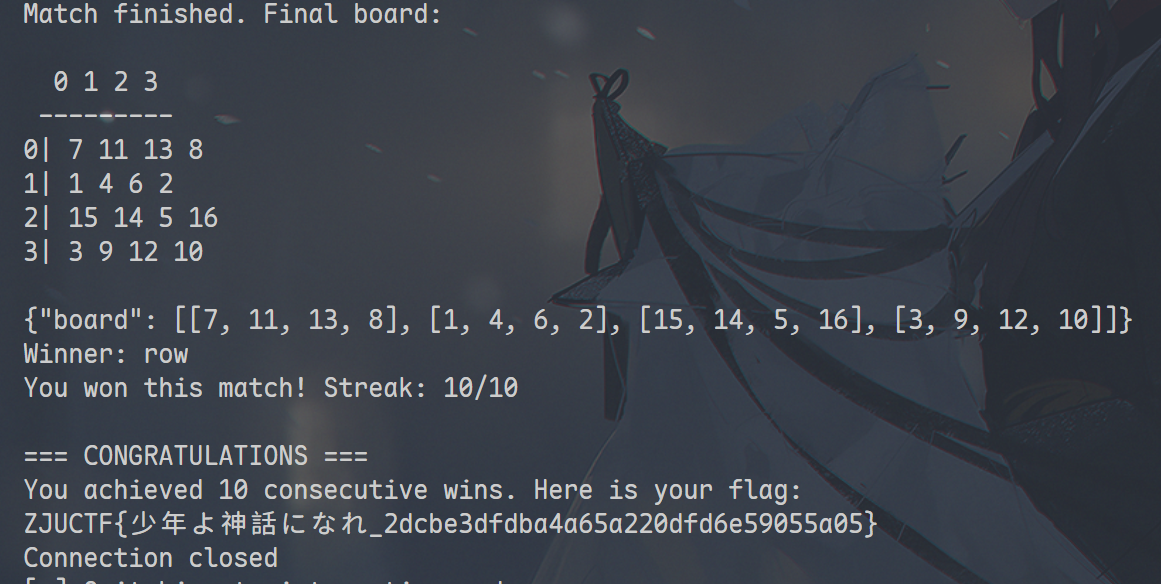
ZJUCTF{ 少年よ神話になれ _2dcbe3dfdba4a65a220dfd6e59055a05}
bingo¶
将语句转化为数学逻辑语句,使用 z3 约束求解(有几个格子我真没看懂啥意思,描述疑似太含糊了,一开始无解,就把那几个注释掉算了,最后恰好只有一解
from z3 import *
s = Solver()
# 1. Variables
x = [[Bool(f'x_{i}_{j}') for j in range(5)] for i in range(5)]
x_int = [[If(x[i][j], 1, 0) for j in range(5)] for i in range(5)]
# 2. Aggregates
row_sums = [Sum(x_int[i]) for i in range(5)]
col_sums = [Sum([x_int[i][j] for i in range(5)]) for j in range(5)]
total_sum = Sum([x_int[i][j] for i in range(5) for j in range(5)])
diag1_sum = Sum([x_int[i][i] for i in range(5)])
diag2_sum = Sum([x_int[i][4-i] for i in range(5)])
# 3. Definitions
primes = {2, 3, 5, 7, 11, 13, 17, 19, 23}
composites = {4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25}
def is_prime(val): return Or([val == p for p in primes])
def is_composite(val): return Or([val == c for c in composites])
row_full = [row_sums[i] == 5 for i in range(5)]
col_full = [col_sums[j] == 5 for j in range(5)]
diag_full = [diag1_sum == 5, diag2_sum == 5]
# Track constraints for UNSAT core
constraints = {}
def add_c(name, cond):
# s.assert_and_track(cond, name)
s.add(cond)
constraints[name] = cond
# Global Constraints
# Exactly one full line
all_full_lines = row_full + col_full + diag_full
# add_c("Global_OneFull", Sum([If(cond, 1, 0) for cond in all_full_lines]) == 1)
# R1C1: 此格为 1,且总勾数为素数
# x[0][0] <-> (x[0][0] AND Prime(Total)) => x[0][0] -> Prime(Total)
add_c("R1C1", x[0][0] == And(x[0][0], is_prime(total_sum)))
# R1C2: 总勾数 >= 12
add_c("R1C2", x[0][1] == (total_sum >= 12))
# R1C3: 第 2 列勾数 <= 第 3 列勾数,且第 2 列与第 3 列勾数奇偶性相同
add_c("R1C3", x[0][2] == And(col_sums[1] <= col_sums[2], col_sums[1] % 2 == col_sums[2] % 2))
# R1C4: 第 1 行勾数 < 第 4 列勾数
add_c("R1C4", x[0][3] == (row_sums[0] < col_sums[3]))
# R1C5: 存在一行被填满
add_c("R1C5", x[0][4] == Or(row_full))
# R2C1: 此格为 1
# If this is just a statement: x[1][0] == x[1][0] (Tautology)
# But if it's the "Logic Start Point", we might enforce x[1][0] == True.
# Let's add the statement definition first.
# The statement "This cell is 1" is true iff x[1][0] is 1.
# So x[1][0] <-> x[1][0].
# We will add the "Start Point" enforcement separately.
# R2C2: total <= 13 XOR 至少两行为奇数
odd_rows_count = Sum([If(row_sums[i] % 2 == 1, 1, 0) for i in range(5)])
add_c("R2C2", x[1][1] == Xor(total_sum <= 13, odd_rows_count >= 2))
# R2C3: 恰好存在 1 行完全为空
empty_rows_count = Sum([If(row_sums[i] == 0, 1, 0) for i in range(5)])
add_c("R2C3", x[1][2] == (empty_rows_count == 1))
# R2C4: 1 不是质数 (True)
add_c("R2C4", x[1][3] == True)
# R2C5: 存在某个 2*2 的区域全为 1
exists_2x2 = False
for r in range(4):
for c in range(4):
block = And(x[r][c], x[r+1][c], x[r][c+1], x[r+1][c+1])
exists_2x2 = Or(exists_2x2, block)
add_c("R2C5", x[1][4] == exists_2x2)
# R3C1: 中心格为 1,且两条对角线上的 1 数为合数
diag_union_count = diag1_sum + diag2_sum - x_int[2][2]
add_c("R3C1", x[2][0] == And(x[2][2], is_composite(diag_union_count)))
# R3C2: 左上 3×3 区域至少 5 个为 1
top_left_sum = Sum([x_int[i][j] for i in range(3) for j in range(3)])
add_c("R3C2", x[2][1] == (top_left_sum >= 5))
# R3C3: 上下相邻均为 1 的格对不少于四对
vert_pairs = []
for j in range(5):
for i in range(4):
vert_pairs.append(If(And(x[i][j], x[i+1][j]), 1, 0))
vert_pairs_count = Sum(vert_pairs)
add_c("R3C3", x[2][2] == (vert_pairs_count >= 4))
# R3C4: 上下相邻均为 1 的格对不多于六对
add_c("R3C4", x[2][3] == (vert_pairs_count <= 6))
# R3C5: 答案不是对角线
add_c("R3C5", x[2][4] == Not(Or(diag_full)))
# R4C1: 此格相邻三格的勾数为偶数
# Neighbors of (3, 0): (2, 0), (4, 0), (3, 1)
neighbors_sum = x_int[2][0] + x_int[4][0] + x_int[3][1]
add_c("R4C1", x[3][0] == (neighbors_sum % 2 == 0))
# R4C2: (a*a + b) % 5 <= 3 且 a <= b
a = row_sums[3]
b = col_sums[1]
add_c("R4C2", x[3][1] == And((a*a + b) % 5 <= 3, a <= b))
# R4C3: 全体勾的重心不偏右
moment = Sum([j * x_int[i][j] for i in range(5) for j in range(5)])
add_c("R4C3", x[3][2] == (moment <= 2 * total_sum))
# R4C4: 此行不是正确答案
add_c("R4C4", x[3][3] == Not(row_full[3]))
# R4C5: 如果没有"请先将本格打勾"的逻辑起点,此题不可解
# We assume this statement is True.
# add_c("R4C5_True", x[3][4] == True)
# And it implies we must start with R2C1
# add_c("StartPoint_R2C1", x[1][0] == True)
# R5C1: 第四列的勾数与第二列的勾数之和为合数
add_c("R5C1", x[4][0] == is_composite(col_sums[3] + col_sums[1]))
# R5C2: 1 不是合数 XOR 此列是正确答案
# 1 is not composite (True). True XOR A = Not A.
# "此列" is Col 2 (index 1).
add_c("R5C2", x[4][1] == Not(col_full[1]))
# R5C3: 此列是勾数唯一最少的列
# Col 3 (index 2).
is_unique_min = And([col_sums[2] < col_sums[j] for j in range(5) if j != 2])
add_c("R5C3", x[4][2] == is_unique_min)
# R5C4: 至少存在某一行连续三个格子打勾且至少存在某一列连续三个格子打勾
def has_consecutive_3(line_vars):
c1 = And(line_vars[0], line_vars[1], line_vars[2])
c2 = And(line_vars[1], line_vars[2], line_vars[3])
c3 = And(line_vars[2], line_vars[3], line_vars[4])
return Or(c1, c2, c3)
row_has_3 = Or([has_consecutive_3(x[i]) for i in range(5)])
col_has_3 = Or([has_consecutive_3([x[i][j] for i in range(5)]) for j in range(5)])
add_c("R5C4", x[4][3] == And(row_has_3, col_has_3))
# R5C5: 不存在某一对角线有至少三个格子打勾
diag1_has_3 = diag1_sum >= 3
diag2_has_3 = diag2_sum >= 3
add_c("R5C5", x[4][4] == Not(Or(diag1_has_3, diag2_has_3)))
print("Checking...", flush=True)
if s.check() == sat:
print("SAT", flush=True)
m = s.model()
ans = []
for i in range(5):
row = [1 if m.evaluate(x[i][j]) else 0 for j in range(5)]
print(row)
ans.append(row)
print("flag: ZJUCTF{", end="")
for i in range(5):
for j in range(5):
print(ans[i][j], end="")
if i != 4:
print("_", end="")
else:
print("}")
else:
print("UNSAT", flush=True)
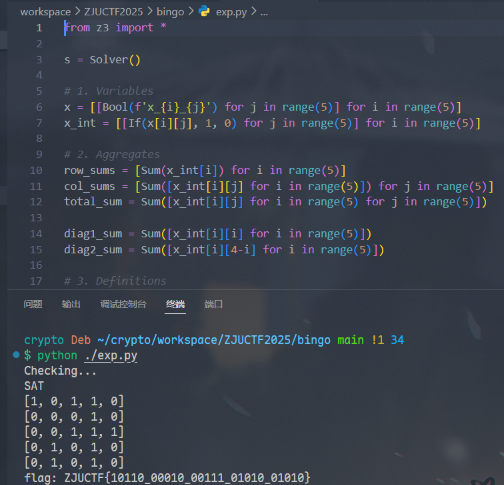
ZJUCTF{10110_00010_00111_01010_01010}
Lab report¶
题目提供了一个 PDF 文件,使用 exiftool -XMP 查看时报错:
$ exiftool -XMP ./1145141919810-Dremig-Lab1.pdf
Warning: Invalid xref table - ./1145141919810-Dremig-Lab1.pdf
查看 PDF 文件末尾的 xref 表:
xref
0 290
0000000000 65535 f
0000000100 00000 n
0000000110 00000 n
0000000130 00000 n
0000000140 00000 n
...
发现偏移量非常规律,计算相邻偏移量的差值:
跳过第一个差值(100
将差值映射为二进制:
- 差值 10 → 二进制 0
- 差值 20 → 二进制 1
每 8 位转换为 ASCII 字符:
01011010 → Z
01001010 → J
01010101 → U
01000011 → C
01010100 → T
01000110 → F
01111011 → {
...
file_path = "./1145141919810-Dremig-Lab1.pdf"
with open(file_path, "rb") as f:
data = f.read()
# Find "xref"
xref_pos = data.find(b"xref")
if xref_pos == -1:
print("No xref found")
exit(0)
print(f"xref found at {xref_pos}")
# Read the lines after xref
lines = data[xref_pos:].splitlines()
try:
range_line = lines[1].decode().strip()
start, count = map(int, range_line.split())
print(f"Range: {start} to {start+count-1} (Count: {count})")
except:
print("Could not parse range line")
exit(0)
offsets = []
for i in range(count):
line = lines[2+i].decode().strip()
parts = line.split()
if len(parts) >= 1:
offsets.append(int(parts[0]))
print(f"Extracted {len(offsets)} offsets.")
# Calculate differences
diffs = []
# Skip the first offset (0) to second offset (100) difference, or just handle it.
for i in range(1, len(offsets) - 1):
diff = offsets[i+1] - offsets[i]
diffs.append(diff)
print("Differences:", diffs[:20], "...")
# Analyze differences
# Check if they are all 10 or 20
unique_diffs = set(diffs)
print("Unique differences:", unique_diffs)
# Try to map 10/20 to binary
# 10 -> 0, 20 -> 1
binary_str = ""
for d in diffs:
if d == 10:
binary_str += "0"
elif d == 20:
binary_str += "1"
else:
binary_str += "?"
print("Binary string:", binary_str[:100], "...")
# Convert binary to text
try:
chars = []
for i in range(0, len(binary_str), 8):
byte = binary_str[i:i+8]
if len(byte) == 8:
chars.append(chr(int(byte, 2)))
text = "".join(chars)
print("Decoded text:", text)
except Exception as e:
print("Error decoding binary:", e)
ZJUCTF{PDF_0ff5e7_c4N_H1D3_m3ss4g3}
ZJU-WLAN-insecure¶
使用 Wireshark 或 tshark 分析流量包,发现包含 4 个 HTTP 请求 / 响应,2 个比较关键:
- 请求 1: 获取挑战值 (get_challenge)
{
"challenge": "517557d10a3aff098a898753317e8ef0b2822540d067490585c41d39d847ed7a",
"client_ip": "10.10.98.98",
"ecode": 0,
...
}
- 请求 2: 登录 (srun_portal)
GET /cgi-bin/srun_portal?callback=jQuery...&action=login&username=3220100721
&password={MD5}5f9601066c7ee059d8fdf0d710c7bc50
&ac_id=3&ip=10.10.98.98
&chksum=a5d4e260a6bd874d7036cb1ed3b251aaef3bd522
&info={SRBX1}KxvFtemc1wBEGdNAbPEfd7s02umxP0Nagix+YxJsqbAEh5/fzuIYqad8xrqKW4yzfA9/I3xGKPMTNziE1wPFhfnCaX8CWsnglgKKjVozxsa46BrEY0n4kc/y2rdlbE7wWPBjdWxaZ4yfs8DLRovR7L==
&n=200&type=1&...
响应:
{
"ecode": 0,
"error": "ok",
"ploy_msg": "E0000: Login is successful.",
"suc_msg": "login_ok",
"username": "3220100721",
...
}
SRUN 系统使用以下加密流程:
- 客户端获取
challenge( 随机 token) - 构造包含用户信息的 JSON 数据:
- 使用 XXTEA 算法和 challenge 作为密钥加密 JSON
- 使用魔改 Base64 编码加密结果
- 添加
{SRBX1}前缀,形成info参数
对于 XXTEA 部分,在 10_0_0_55_login 找到了对应内容
import math
import json
from base64 import b64decode
# https://github.com/Aloxaf/10_0_0_55_login/blob/master/10_0_0_55.py
from 10_0_0_55 import fkbase64, xencode
def decrypt_info(info_str, token):
if info_str.startswith("{SRBX1}"):
info_str = info_str[7:]
encrypted_data = fkbase64_decode(info_str)
print(f"Base64 ({len(encrypted_data)} bytes): {encrypted_data.hex()[:80]}...")
try:
decrypted_data = xdecode(encrypted_data, token)
print(f"XXTEA decode ({len(decrypted_data)} bytes)")
result = decrypted_data.decode('utf-8')
print(f"\tJSON: {result}")
return result
except Exception as e:
print(f"failed: {e}")
import traceback
traceback.print_exc()
return None
# 从流量包中提取的数据
info = "{SRBX1}KxvFtemc1wBEGdNAbPEfd7s02umxP0Nagix+YxJsqbAEh5/fzuIYqad8xrqKW4yzfA9/I3xGKPMTNziE1wPFhfnCaX8CWsnglgKKjVozxsa46BrEY0n4kc/y2rdlbE7wWPBjdWxaZ4yfs8DLRovR7L=="
token = "517557d10a3aff098a898753317e8ef0b2822540d067490585c41d39d847ed7a"
print(f"Token: {token}")
print(f"Info: {info[:60]}...")
result = decrypt_info(info, token)
if result:
try:
data = json.loads(result)
# for key, value in data.items():
# print(f"\t{key}: {value}")
# print()
password = data.get('password', '')
if password:
print(password)
except Exception as e:
print(f"failed: {e}")
else:
print("failed")

ZJUCTF{Thanks, TLS!}