3 KNN
k- 近邻算法,通常简称为 kNN,是一种基本且直观的机器学习算法。它既可以用于分类任务,也可以用于回归任务。它的核心思想非常简单:一个样本的类别由其在特征空间中最近的 k 个邻居的类别决定。
历史背景
kNN 算法由 T. M. Cover 和 P. E. Hart 在 1967 年的一篇论文中首次提出,是机器学习领域最基础的算法之一。它是一种非参数1、基于实例2 的学习方法。
论文引用 : T. M. Cover, P. E. Hart, Nearest neighbor pattern classification, IEEE Transactions on Information Theory, 13 (1): 21–27, 1967.
k 近邻法 (k-Nearest Neighbors, kNN) (page 2-3) ¶
定义与工作原理 (page 2-3) ¶
kNN 算法的逻辑可以通俗地理解为“物以类聚,人以群分”。
kNN 算法定义
给定一个包含标签的训练数据集。当一个新的、没有标签的实例输入时,我们在训练数据集中找到与该实例特征最相似(即距离最近)的 k 个实例。然后,根据这 k 个实例的标签进行投票,将得票最多的类别作为新实例的预测类别。
其工作原理可以概括为以下三步:
- 准备数据:存在一个已经标记好类别的训练样本集。
- 计算距离:当输入一个新样本时,计算它与训练集中每一个样本的距离。
- 确定邻居并决策:找出距离最近的 k 个样本(即 k 个近邻
) ,然后根据这 k 个邻居的标签,通过多数表决等方式,决定新样本的类别。
Note
在实际应用中,k 的取值通常不大,例如一般不超过 20。
k 近邻法的三要素 (page 2) ¶
要实现 kNN 算法,必须明确以下三个核心要素:
- k 的选择:如何选择邻居的数量 k。
- 距离度量:如何衡量样本之间的“远近”。
- 分类决策规则:如何根据 k 个邻居的标签做出最终决策。
算法描述 (page 4) ¶
我们可以将 kNN 算法用更规范的数学语言来描述。
算法 3.1 (k 近邻法 )
输入:
- 训练数据集 \(T = \{(x_1, y_1), (x_2, y_2), \dots, (x_N, y_N)\}\),其中 \(x_i \in \mathcal{X} \subseteq \mathbb{R}^n\) 是实例的特征向量, \(y_i \in \mathcal{Y} = \{c_1, c_2, \dots, c_K\}\) 是实例的类别。
- 新的实例特征向量 \(x\)。
输出:实例 \(x\) 的所属类别 \(y\)。
步骤:
- 根据选定的距离度量,在训练集 \(T\) 中找出与 \(x\) 最邻近的 \(k\) 个点,将这 \(k\) 个点构成的集合记作 \(N_k(x)\)。
- 在 \(N_k(x)\) 中根据分类决策规则(例如多数表决)来确定 \(x\) 的类别 \(y\)。对于多数表决,类别 \(y\) 的计算公式如下:
其中,\(I(\cdot)\) 是指示函数 (indicator function),当括号内的条件成立时取值为 1,否则为 0。这个公式的含义是,找出在 k 个近邻中出现次数最多的那个类别。
最近邻算法
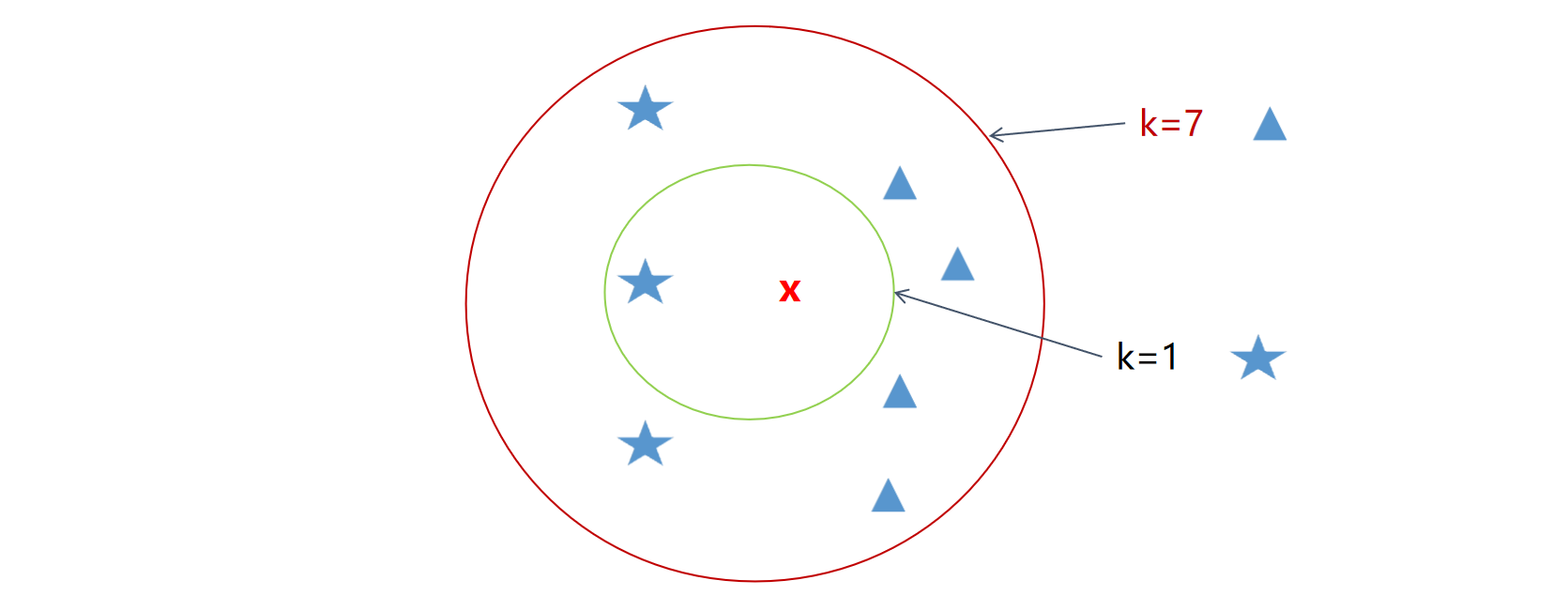
当 \(k=1\) 时,kNN 算法就退化为最近邻算法 (Nearest Neighbor Algorithm)。此时,新实例的类别直接由其最近的那个训练样本的类别决定。如下图所示,如果 k=1,新实例 x(红色叉)将被归为蓝色五角星一类;如果 k=7,则其邻域内(红色圆圈)包含了 4 个蓝色三角形和 3 个蓝色五角星,因此将被归为蓝色三角形一类。
k 近邻法的应用 (page 6-7) ¶
kNN 算法因其简单直观,在许多领域都有应用,尤其是在分类问题上。例如:
- 电影分类:根据电影的打斗镜头数、爱情镜头数等特征,将其归类为动作片、爱情片等。
- 图像识别:识别图片中的物体,例如将各种鱼的图片进行分类。
- 文本分类:根据文本中词语出现的频率,判断其属于新闻、体育还是娱乐等类别。
k 近邻法特点 (page 8) ¶
kNN 算法有其独特的优缺点。
优点 (page 8) ¶
- 简单易懂:算法原理直观,实现简单。
- 适应性强:可用于分类和回归任务,并且对数据类型没有特殊要求。
- 无假设分布:作为非参数模型,它不对数据分布做任何假设,因此能很好地处理非线性关系的数据。
缺点 (page 8) ¶
- 计算成本高:在预测阶段,需要计算新样本与所有训练样本的距离,当训练集非常大时,计算开销巨大。
- 对噪声敏感:特别是当 k 值较小时,模型容易受到噪声数据或异常值的影响,因为决策是基于非常局部的区域。
- 需要选择合适的 k 值:k 值的选择对模型性能影响巨大。过小的 k 值容易导致过拟合,而过大的 k 值容易导致欠拟合。
- 样本不平衡问题:当训练集中不同类别的样本数量相差悬殊时,kNN 倾向于将新样本预测为数量占优的多数类,对少数类的预测效果较差。
kNN 三要素详解 ¶
k 值的选择 (page 9) ¶
k 值的选择是一个关键问题,它直接影响模型的复杂度和预测效果。
-
较小的 k 值:
- 模型会变得更复杂,因为它只考虑了非常局部的实例。
- 优点:能够学习到更精细的决策边界。
- 缺点:对噪声点非常敏感,容易发生过拟合。想象 \(k=1\) 时,一个噪声点就可能改变其周围新样本的预测结果。
-
较大的 k 值:
- 模型会变得更简单,因为它考虑了更大范围的实例。
- 优点:具有更好的鲁棒性,能够减少噪声的影响。
- 缺点:可能会忽略数据中局部、细微的模式,导致决策边界过于平滑,发生欠拟合。
如何选择 k 值?
在实际应用中,k 值通常不大,并且一般通过交叉验证 (Cross-validation) 的方法来选取。例如,可以将数据集划分为训练集(如 90%)和验证集(如 10%
分类决策规则 (page 10) ¶
最常用的决策规则是多数表决 (majority voting rule)。这个规则不仅直观,而且在理论上与经验风险最小化相关联。
多数表决与经验风险最小化
假设我们使用 0-1 损失函数作为模型的损失函数。这意味着,当分类正确时损失为 0,分类错误时损失为 1。
对于一个给定的实例 \(x\),假设它的 k 个最近邻居的集合是 \(N_k(x)\)。如果我们预测它的类别为 \(c_j\),那么在这个邻域内的误分类率(即经验风险)可以表示为:
为了最小化这个经验风险,我们只需要最大化分类正确的数量。
因此,要使误分类率最小,就需要使 \(\sum_{x_i \in N_k(x)} I(y_i = c_j)\) 最大化。这正是多数表决规则的数学表达:选择在 k 个邻居中出现次数最多的类别。
距离度量 (page 11) ¶
距离度量用于衡量特征空间中两个样本点的相似程度。不同的距离度量可能会导致不同的近邻选择,从而影响最终的分类结果。
常用的距离是 \(L_p\) 距离 (Lp distance) 或称 闵可夫斯基距离 (Minkowski distance)。 设有两个 n 维向量 \(x_i = (x_i^{(1)}, x_i^{(2)}, \dots, x_i^{(n)})^T\) 和 \(x_j = (x_j^{(1)}, x_j^{(2)}, \dots, x_j^{(n)})^T\),它们之间的 \(L_p\) 距离定义为:
\(L_p\) 距离在不同的 \(p\) 值下有不同的特例:
-
欧式距离 (Euclidean Distance, \(p=2\)):这是最常用的距离度量,代表了两个点在空间中的直线距离。
\[ L_2(x_i, x_j) = \left( \sum_{l=1}^{n} |x_i^{(l)} - x_j^{(l)}|^2 \right)^{\frac{1}{2}} \] -
曼哈顿距离 (Manhattan Distance, \(p=1\)):也称为城市街区距离,表示在标准坐标系下,从一个点到另一个点需要经过的街区距离之和。
\[ L_1(x_i, x_j) = \sum_{l=1}^{n} |x_i^{(l)} - x_j^{(l)}| \] -
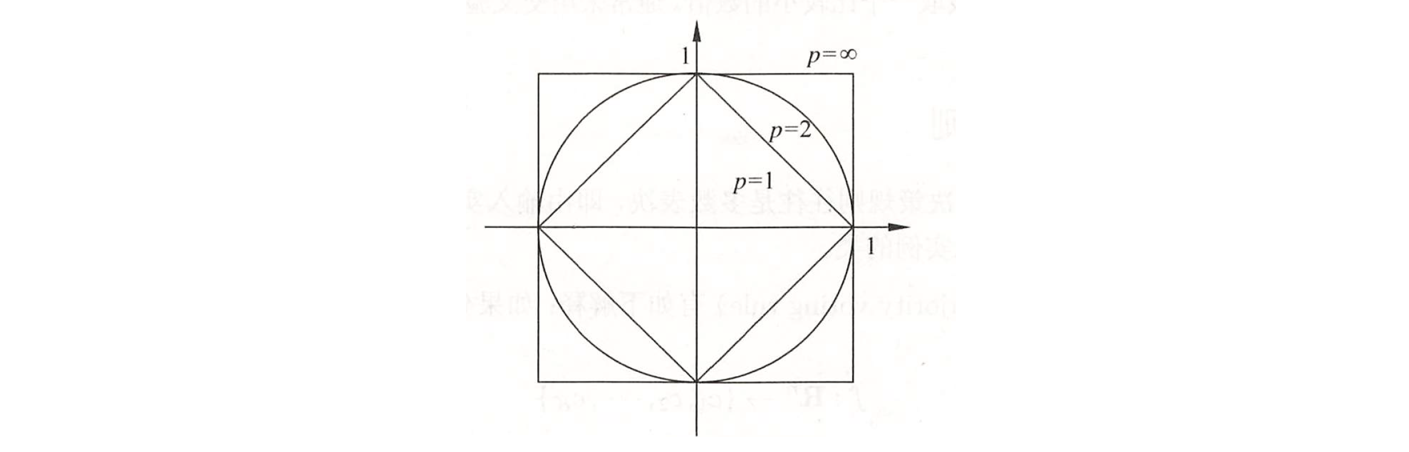
切比雪夫距离 (Chebyshev Distance, \(p=\infty\)):当 \(p \to \infty\) 时, \(L_p\) 距离收敛到此距离,它等于两个点在各个坐标上差值的最大值。
\[ L_\infty(x_i, x_j) = \max_{l} |x_i^{(l)} - x_j^{(l)}| \]
上图直观地展示了二维空间中,到原点的 \(L_p\) 距离为 1 的点的集合构成的图形。\(p=2\) 是圆形, \(p=1\) 是菱形, \(p=\infty\) 是正方形。
( 例 3.1) 已知二维空间中的 3 个点: \(x_1 = (1,1)^T\), \(x_2 = (5,1)^T\), \(x_3 = (4,4)^T\)。试求在不同 \(p\) 值下, \(x_1\) 的最近邻点是哪个?
解: 1. 计算 \(x_1\) 和 \(x_2\) 的 \(L_p\) 距离: 因为 \(x_1\) 和 \(x_2\) 只有一个维度不同,所以它们的 \(L_p\) 距离为: \(L_p(x_1, x_2) = (|1-5|^p + |1-1|^p)^{1/p} = (|4|^p)^{1/p} = 4\)。这个距离与 \(p\) 无关。
-
计算 \(x_1\) 和 \(x_3\) 的 \(L_p\) 距离: \(L_p(x_1, x_3) = (|1-4|^p + |1-4|^p)^{1/p} = (3^p + 3^p)^{1/p} = (2 \cdot 3^p)^{1/p} = 3 \cdot 2^{1/p}\)。
-
比较距离:
- 当 \(p=1\) 时 , \(L_1(x_1, x_3) = 3 \cdot 2^1 = 6\)。因为 \(4 < 6\),所以 \(x_2\) 是最近邻点。
- 当 \(p=2\) 时 , \(L_2(x_1, x_3) = 3 \cdot \sqrt{2} \approx 4.24\)。因为 \(4 < 4.24\),所以 \(x_2\) 仍然是最近邻点。
- 当 \(p=3\) 时 , \(L_3(x_1, x_3) = 3 \cdot 2^{1/3} \approx 3.78\)。因为 \(4 > 3.78\),所以 \(x_3\) 变成了最近邻点。
结论:距离度量的选择会改变谁是“最近邻”,从而可能改变 kNN 的预测结果。
度量学习 (page 14-15,考试不涉及 ) ¶
既然距离度量如此重要,我们能否不手动选择一个,而是让算法学习出一个最适合当前任务的距离度量呢?这就是度量学习 (Distance Metric Learning) 的研究内容。
其核心思想是学习一个距离函数,使得在新的度量下,同类样本之间的距离尽可能小,而异类样本之间的距离尽可能大。一个常见的度量学习方法是学习一个马氏距离 (Mahalanobis Distance)。
马氏距离的形式如下:\(D_M(x_i, x_j) = \sqrt{(x_i - x_j)^T M (x_i - x_j)}\)
其中 \(M\) 是一个半正定矩阵。学习马氏距离就等价于学习这个矩阵 \(M\)。
度量学习模型
- 模型 1 (Xing et. al 2002):该模型的目标是最大化异类点对之间的距离之和,同时约束同类点对的距离之和在一个常数(如 1)以内。
- 模型 2 (Weinberger & Saul 2009, LMNN):该模型的目标是,对于每个样本 \(x_i\),其目标邻居(同类)要比入侵者(异类)离它更近,并且保持一个安全间隔(margin
) 。同时,它也会拉近目标邻居的距离。这是一种基于大间隔思想的度量学习。
kNN 面临的挑战与优化 (page 16) ¶
kNN 算法虽然简单,但在实际应用中面临一些挑战,其中最主要的就是复杂度问题。
kNN 的复杂度挑战 ¶
在预测阶段,kNN 需要:
- 计算新样本与训练集中 N 个样本的距离,时间复杂度为 \(O(N \cdot d)\),其中 \(d\) 是特征维度。
- 找到距离最近的 k 个样本,如果用排序法,复杂度是 \(O(N \log N)\)。
当 N 非常大时,这个计算成本是无法接受的。为了解决这个问题,研究者们提出了使用 kd 树 (k-dimensional tree) 等数据结构来加速最近邻的搜索。
kd 树 (k-dimensional tree) (page 17-18) ¶
Attention
kd 树中的“k”指的是数据空间的维度 (dimension),而 kNN 算法中的“k”指的是邻居的数量 (number of neighbors)。两者含义完全不同。
kd 树是一种用于组织 k 维空间中点集的二叉树数据结构。它的主要目的是实现高效的最近邻搜索。
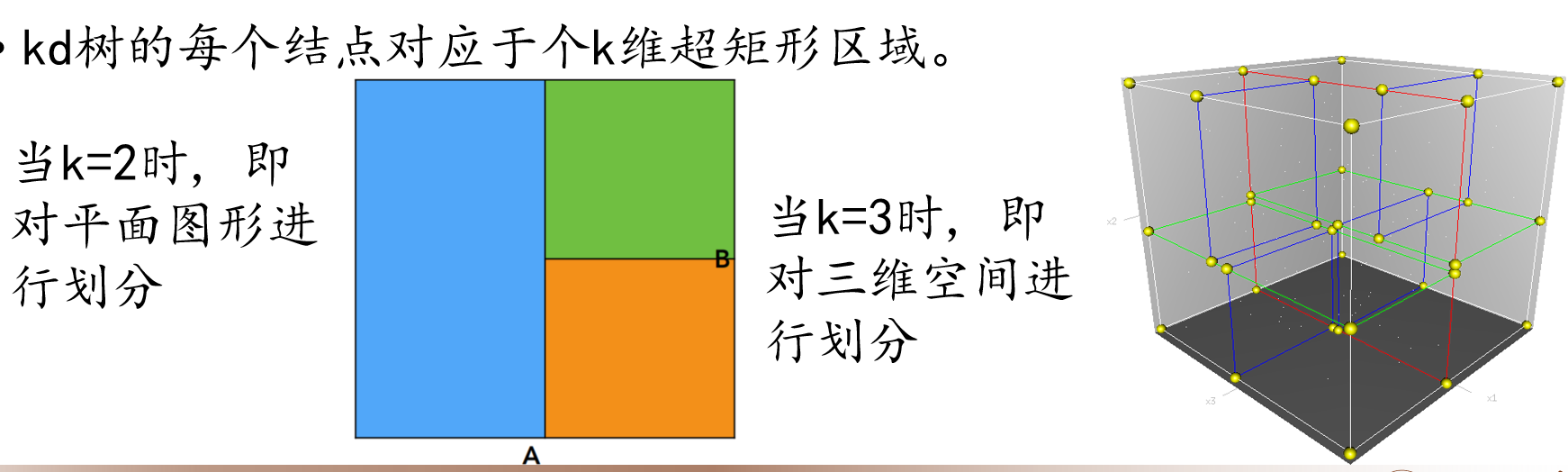
核心思想:通过轮流选择坐标轴并取中位数点进行切分,不断地将 k 维空间划分为一系列互不重叠的 k 维超矩形区域。树中的每个节点都对应于一个这样的超矩形区域。
- 当 \(k=2\) 时,kd 树对平面进行划分。
- 当 \(k=3\) 时,kd 树对三维空间进行划分。
构造 kd 树 (page 19) ¶
构造一个平衡的 kd 树的算法步骤如下:
算法 3.2 ( 构造平衡 kd 树 )
输入:k 维空间数据集 \(T = \{x_1, x_2, \dots, x_N\}\)
输出:kd 树
步骤:
1. 确定分裂维度:从根节点开始(深度 \(j=0\)
构造示例 (page 20) ¶
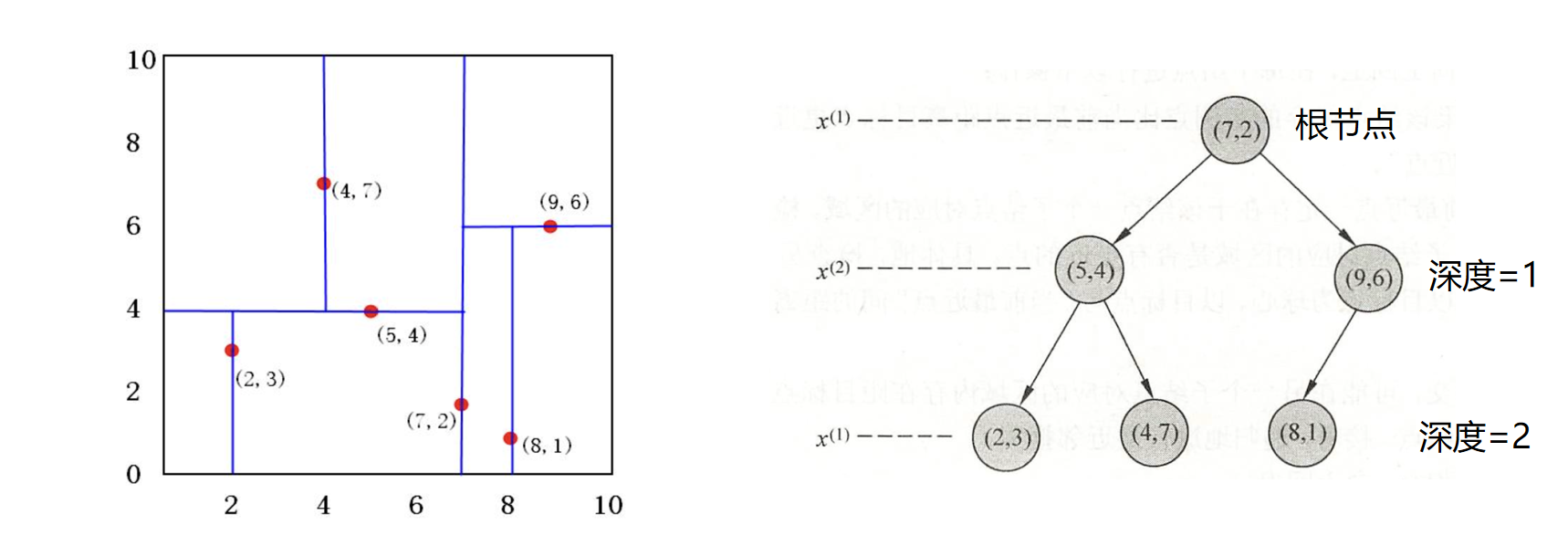
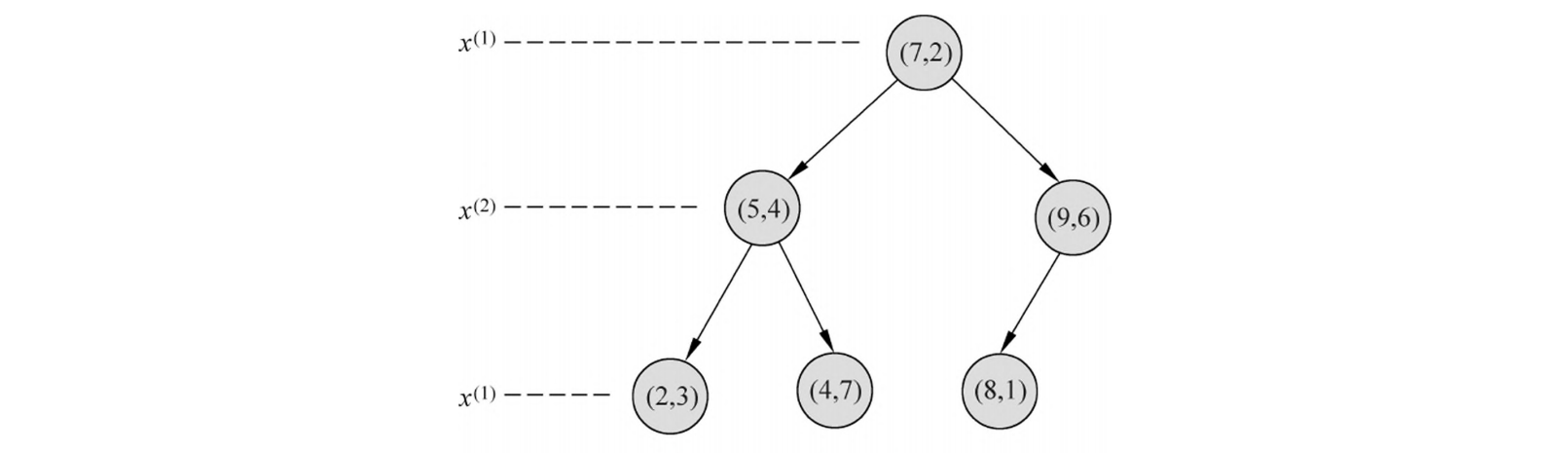
( 例题 3.2) 给定数据集 \(T = \{(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)\}\),构造 kd 树的过程如下:
-
根节点 ( 深度 0):
- 分裂维度 \(l = 0 \pmod 2 + 1 = 1\) (x 轴 )。
- 所有点的 x 坐标为。中位数是 7。选择点 (7,2) 作为根节点。
- 小于 7 的点 \(\{(2,3), (5,4), (4,7)\}\) 进入左子树;大于 7 的点 \(\{(9,6), (8,1)\}\) 进入右子树。
-
左子树 ( 深度 1):
- 数据集为 \(\{(2,3), (5,4), (4,7)\}\)。
- 分裂维度 \(l = 1 \pmod 2 + 1 = 2\) (y 轴 )。
- y 坐标为。中位数是 4。选择点 (5,4) 作为节点。
- 小于 4 的点 \(\{(2,3)\}\) 进入左子树;大于 4 的点 \(\{(4,7)\}\) 进入右子树。
-
右子树 ( 深度 1):
- 数据集为 \(\{(9,6), (8,1)\}\)。
- 分裂维度 \(l = 1 \pmod 2 + 1 = 2\) (y 轴 )。
- y 坐标为。中位数是 1 或 6,这里选择 (9,6) 作为节点。
- 点 \(\{(8,1)\}\) 进入左子树。
最终形成的 kd 树和空间划分如下图所示:
kd 树的最近邻搜索 (page 21) ¶
使用 kd 树进行最近邻搜索比暴力搜索要高效得多。其过程包含“向下查找”和“向上回溯”两个阶段。
算法 3.3 ( 用 kd 树的最近邻搜索 )
输入:已构造的 kd 树,目标点 \(x\)
输出:\(x\) 的最近邻点
步骤:
1. 向下查找:从根节点出发,根据目标点 \(x\) 在当前节点分裂维度上的坐标值,决定是进入左子树还是右子树(小于分裂值进左,大于等于进右
搜索示例 (page 22-25) ¶
示例 1:求点 \((2.1, 3.1)^T\) 的最近邻点
- 向下查找:
- 根 (7,2),分裂轴 x=7。2.1 < 7,去左子树。
- 节点 (5,4),分裂轴 y=4。3.1 < 4,去左子树。
- 到达叶子节点 (2,3)。
- 设置当前最优:当前最近邻点是 (2,3),距离为 \(L_2((2.1,3.1), (2,3)) = \sqrt{0.1^2 + 0.1^2} \approx 0.1414\)。
- 向上回溯:
- 回溯到 (5,4)。以 (2.1,3.1) 为圆心,0.1414 为半径的圆,不与 y=4 的分割线相交。因此,(5,4) 的右子空间(包含 (4,7) 的区域)被剪枝,无需搜索。
- 回溯到 (7,2)。以 (2.1,3.1) 为圆心,0.1414 为半径的圆,不与 x=7 的分割线相交。因此,(7,2) 的右子空间被剪枝。
- 结束:回溯到根,搜索结束。最近邻点为 (2,3)。
示例 2:求点 \((2, 4.5)^T\) 的最近邻点
- 向下查找:
- 根 (7,2),x=7。2 < 7,去左。
- 节点 (5,4),y=4。4.5 > 4,去右。
- 到达叶子 (4,7)。
- 设置当前最优:当前最近邻点是 (4,7),距离为 \(L_2((2,4.5), (4,7)) = \sqrt{2^2 + 2.5^2} \approx 3.202\)。
- 向上回溯:
- 回溯到 (5,4)。计算距离 \(L_2((2,4.5), (5,4)) = \sqrt{3^2 + 0.5^2} \approx 3.041\)。这个距离更小!更新最近邻点为 (5,4),最近距离为 3.041。
- 检查兄弟区域:以 (2,4.5) 为圆心,3.041 为半径的圆,与 (5,4) 的分割线 y=4 相交。因此,必须进入 (5,4) 的左子树(包含 (2,3) 的区域)进行搜索。
- 进入兄弟区域:
- 从 (5,4) 的左子节点 (2,3) 开始搜索。计算距离 \(L_2((2,4.5), (2,3)) = \sqrt{0^2 + 1.5^2} = 1.5\)。这个距离更小!再次更新最近邻点为 (2,3),最近距离为 1.5。
- 继续回溯:
- 从 (2,3) 回溯到 (5,4),再回溯到根 (7,2)。计算距离 \(L_2((2,4.5), (7,2)) = \sqrt{5^2 + 2.5^2} \approx 5.59\),比 1.5 大,不更新。
- 检查兄弟区域:以 (2,4.5) 为圆心,1.5 为半径的圆,不与 (7,2) 的分割线 x=7 相交。因此,根节点的右子树被剪枝。
- 结束:回溯到根,搜索结束。最终最近邻点为 (2,3),距离为 1.5。
习题 3.2 ¶
Question
利用例题 3.2 的构造的 kd 树求点 \(x = (3, 4.5)^T\) 的最近邻点。
- 二叉树搜索:先从 (7, 2) 点开始进行二叉查找,然后到达 (5, 4),最后到达 (4, 7),此时搜索路径中的结点为 < (7, 2),(5, 4),(4, 7) >,首先以 (4, 7) 作为当前最近邻点,计算其到查询点 (3, 4.5) 的距离为 2.69。
- 回溯查找
: (1)在得到 (4, 7) 为查询点的最近点后,回溯到其父结点 (5, 4),计算其到查询点 (3, 4.5) 的距离为 2.06,小于 2.69,则父结点 (5, 4) 比 (4, 7) 距离查询点更近; (2)更新 (5, 4) 为当前最近邻点,并判断在该父结点的其他子结点空间中是否有距离查询点更近的数据点。以 (3, 4.5) 为圆心,以 2.06 为半径画圆,发现该圆和超平面 y = 4 交割,因此进入 (5, 4) 结点的左子空间中去搜索; (3)计算 (2, 3) 到查询点 (3, 4.5) 的距离为 1.80,小于 2.06,则点 (2, 3) 比 (5, 4) 距离查询点更近,更新 (2, 3) 为当前最近点。 - 最后,再回溯到 (7, 2),以 (3, 4.5) 为圆心,以 1.80 为半径的圆不与 x = 7 超平面交割,因此不用进入 (7, 2) 右子空间进行查找。至此,搜索路径中的结点已经全部回溯完,结束整个搜索,返回最近邻点 (2, 3),最近距离为 1.80。