5 Decision Tree
决策树(Decision Tree)是机器学习领域中一种非常基础且应用广泛的算法。它既可以用于分类问题,也可以用于回归问题。其核心思想源于人类在做决策时,往往会根据一系列问题(或条件)进行判断,最终得出一个结论。决策树模型就是将这个过程进行了形式化和算法化。
决策树的定义 (page 2-3) ¶
决策树
决策树 (decision tree) 是一种基本的分类与回归方法。其模型呈树形结构,可以被看作是一系列 if-then 规则的集合,具有很强的可解释性。
决策树主要由以下几个部分构成:
- 结点 (Node):
- 内部结点 (Internal Node): 每个内部结点代表对一个特征或属性的测试。它通常包含一个问题,例如“年龄是否小于 30
? ”或“是否有房? ”。 - 叶结点 (Leaf Node): 也称为终端结点 (Terminal Node),代表一个类别(在分类树中)或一个具体的数值(在回归树中
) 。它代表了最终的决策结果。
- 内部结点 (Internal Node): 每个内部结点代表对一个特征或属性的测试。它通常包含一个问题,例如“年龄是否小于 30
- 有向边 (Directed Edge): 代表根据内部结点测试结果划分出的不同分支。每条边通常对应着特征的一个可能取值。
整个决策过程从根结点 (Root Node) 开始,将待分类的实例(数据)的某个特征代入根结点的测试条件中,根据测试结果,沿着对应的分支向下传递。这个过程在后续的内部结点上递归地进行,直到实例被分配到某一个叶结点为止。该叶结点的标签就是这个实例的预测结果。
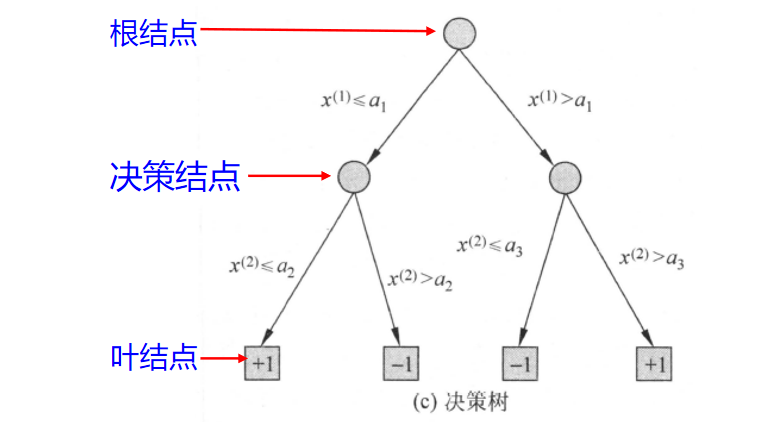
上图直观地展示了决策树的组成部分。从根结点开始,根据特征 x(1) 的取值将数据划分,接着在子结点上根据特征 x(2) 继续划分,最终到达叶结点 +1 或 -1,完成分类。
例子 (page 4-5) ¶
为了更好地理解决策树的工作原理,我们可以看一个生活化的例子。
相亲决策
母亲要给女儿介绍一个男朋友,女儿通过一系列问题来决定是否要去见他。
- 女儿: 多大年纪了?
- 母亲: 26。 (
年龄 <= 30) - 女儿: 长的帅不帅?
- 母亲: 挺帅的。 (
长相 = 帅或中等) - 女儿: 收入高不?
- 母亲: 不算很高,中等情况。 (
收入 = 中等) - 女儿: 是公务员不?
- 母亲: 是,在税务局上班呢。 (
公务员 = 是) - 女儿: 那好,我去见见。 (
决策 = 见)
这个对话过程就可以用一棵决策树来表示,在这个决策树中:
- 内部结点(绿色圆形
) :代表判断条件,如“年龄”、 “长相”、 “收入”、 “公务员”。 - 叶结点(橙色方框
) :代表最终决策,即“见”或“不见”。
分类与回归 (page 6) ¶
决策树可以处理两种主要的机器学习任务,其根本区别在于目标变量(也就是我们希望预测的那个值 y)的类型。
- 分类树 (Classification Tree): 用于处理离散型目标变量。例如,在动物分类的数据集中
, “类标号”(如哺乳动物、爬行类、鸟类)就是离散的。分类树的叶结点输出的是一个类别。 - 回归树 (Regression Tree): 用于处理连续型目标变量。例如,预测房价、股票价格或温度,这些目标变量都是连续的数值。回归树的叶结点输出的是一个具体的数值,通常是该叶结点所有样本目标值的平均值。
Note
在上图中,特征(X)包括体温、表皮覆盖等,而目标属性(y)“类标号”是离散的,因此构建的是一棵分类树。如果目标是预测动物的“平均寿命”(一个连续值
决策树 - 解决分类问题的一般方法 (page 7-8) ¶
构建和使用一个分类模型,通常遵循以下两个主要步骤:
-
模型构建 ( 归纳过程 ):
- 这个阶段也称为学习或训练。
- 我们使用一个带有已知类别标签的训练集 (Training Set)。
- 学习算法通过对训练集的归纳,自动地构建出一个分类模型(例如,一棵决策树
) 。这个过程的目标是找到能够最好地拟合训练数据的规则。
-
预测应用 ( 推论过程 ):
- 这个阶段也称为测试或推理。
- 我们使用已经构建好的模型,对没有类别标签的测试集 (Test Set) 或新数据进行预测。
- 模型根据新数据的特征,推论出其最可能的类别。
决策树学习的步骤 (page 9) ¶
决策树的学习过程,本质上是通过一系列规则对数据进行分类的过程。这个过程通常包含以下三个核心步骤:
- 特征选择 (Feature Selection):
- 特征选择是决定用哪个特征来划分当前数据集。如果把决策树的构建看作是盖房子,特征选择就是决定先用哪根柱子作支撑。
- 好的特征能够将不同类别的数据尽可能地分离开。
- 选择的标准通常是使得划分后的数据集“纯度”最高。后续会介绍如何用信息增益、信息增益比或基尼指数来度量。
- 决策树的生成 (Tree Generation):
- 这是一个递归的过程。从根结点开始,基于特征选择的结果,对数据集进行划分,生成子结点。
- 对每个子结点,重复特征选择和划分的过程,直到满足停止条件。
- 停止条件通常是:
- 当前结点所有样本都属于同一类别。
- 没有剩余特征可供划分。
- 达到预设的树深度或叶结点样本数。
- 决策树的剪枝 (Tree Pruning):
- 直接根据训练数据生成的决策树可能会非常复杂,对训练数据拟合得很好,但在新数据上表现不佳,这种现象称为过拟合 (Overfitting)。
- 剪枝是为了简化决策树,去掉一些不必要的枝叶,以提高模型的泛化能力1。
决策树与条件概率分布 (page 10-12) ¶
从概率论的角度看,决策树的学习过程实际上是在划分特征空间,并估计每个划分单元上的条件概率分布 \(P(Y|X)\)。
- 特征空间划分: 决策树的每个内部结点和它引出的分支,都在对特征空间进行一次划分。例如,一个特征
年龄 < 30将整个特征空间分成了两部分。 - 路径与单元: 从根结点到每个叶结点的路径,唯一地定义了特征空间中的一个单元 (cell) 或区域 (region)。这些单元互不相交,并覆盖了整个特征空间。
- 条件概率: 在每个单元(即每个叶结点)内,都定义了一个类的概率分布。这个分布通常是通过该单元内训练样本的类别频率来估计的。例如,一个叶结点包含 8 个“是”类样本和 2 个“否”类样本,那么可以估计在该单元内 \(P(Y=\text{"是"}) = 0.8\),\(P(Y=\text{"否"}) = 0.2\)。
视图的对应关系
- (a) 特征空间划分: 将二维特征空间
(x(1), x(2))划分为 5 个互不相交的矩形单元。每个单元内的+1或-1代表该区域的多数类别。 - (b) 条件概率分布: 在 (a) 的划分基础上,展示了给定特征
X(即某个单元)条件下,类别Y为+1的条件概率 \(P(Y=+1|X)\)。概率越高,立方体的高度越高。 - (c) 决策树: 是一棵与 (a) 和 (b) 完全对应的决策树。树的每个分支都对应一次空间划分。
决策树学习的本质是从训练数据中归纳出一组分类规则。理想情况下,我们希望找到一个与训练数据矛盾尽可能小、同时又具有良好泛化能力的决策树。
决策树算法 (page 14) ¶
决策树的发展历史中,涌现出了一系列经典算法,它们在特征选择、树的生成和剪枝等方面各有侧重。
著名决策树算法
- CLS (Concept Learning System): 1966 年由 Hunt 等人提出,是决策树算法的早期原型。
- ID3 (Iterative Dichotomiser 3): 1979 年由 Ross Quinlan 提出,以信息增益作为特征选择的标准,是决策树发展史上的一个里程碑。
- C4.5: Quinlan 在 ID3 基础上于 1993 年提出的改进算法。它使用信息增益比来克服 ID3 偏向于选择多值特征的缺点,并且可以处理连续值特征和缺失值。
- CART (Classification and Regression Trees): 由 Breiman 等人在 1984 年提出。它非常独特,生成的决策树都是二叉树。对于分类树,它使用基尼指数作为划分标准;对于回归树,它使用平方误差最小化。
决策树 CLS 算法 (page 15-23) ¶
CLS(Concept Learning System)是最早的决策树学习算法之一,为后来的 ID3 等算法奠定了基础。
CLS 基本思想 (page 15) ¶
CLS 采用“分而治之”的策略,其基本思想可以概括为:
- 从一个空树开始,将整个训练样本集视为根结点。
- 选择一个属性作为测试属性,根据该属性的不同取值,将样本集分割成若干子集。
- 对每个子集:
- 如果子集中的所有样本都属于同一类别,则将该子集标记为叶结点,其类别即为该样本的类别。
- 如果子集为空,也标记为叶结点,类别通常设为其父结点中最多的类别。
- 如果子集包含多种类别的样本,则将该子集视为一个新的内部结点,并递归地选择新的属性对其进行划分。
- 重复此过程,直到所有子集都被正确分类或没有属性可用。
CLS 算法步骤 (page 19)
- 初始化: 生成一棵空决策树和完整的训练样本属性集。
- 终止条件检查: 若当前训练集
T中所有样本都属于同一类,则生成一个叶结点,算法终止。 - 属性选择: 否则,根据某种策略选择一个属性
A作为测试属性,生成一个测试结点。 - 数据划分: 根据属性
A的不同取值 {\(v_1, v_2, \dots, v_m\)},将T划分为m个子集 {\(T_1, T_2, \dots, T_m\)}。 - 属性移除: 从属性表中删除属性
A。 - 递归: 对每个子集
T_i,递归调用 CLS 算法(从步骤 2 开始) 。
CLS 算法的问题 (page 20-23) ¶
CLS 算法的一个核心问题是:它没有明确规定如何选择最佳的测试属性。在步骤 3 中,如果只是随机选择或按固定顺序选择,生成的决策树的结构和效率可能会天差地别。
属性选择的重要性
假设有一个学生膳食与缺钙情况的数据集(page 21
- 如果选择“鸡肉”
、 “猪肉”、 “牛肉”等属性来构建树,可能会得到一棵非常复杂、深度很大的树(page 22) 。 - 而如果首先选择“牛奶”这个属性,我们可能会发现,喝牛奶的学生都不缺钙,不喝牛奶的学生大部分都缺钙。这样,仅用一个属性就得到了一个非常简洁且有效的划分(page 23
) 。
实践证明,测试属性的选择顺序对决策树的规模和性能有举足轻重的影响。一个好的选择标准是后续 ID3、C4.5 等算法改进的关键。
决策树 ID3 算法 (page 24) ¶
ID3 算法由 Ross Quinlan 于 1979 年提出,它正是为了解决 CLS 算法中“如何选择最佳属性”的问题。ID3 的核心是使用信息增益 (Information Gain) 作为特征选择的准则。
要理解信息增益,首先需要了解信息论中的两个基本概念:信息量和熵。
信息与不确定性
信息的核心价值在于消除不确定性。一个事件发生的概率越小,它所包含的信息量就越大。例如
熵 (Entropy) (page 25-27) ¶
在信息论中,熵是度量随机变量不确定性的指标。一个系统越混乱、越不确定,其熵值就越高。
信息量与熵
-
信息量: 事件 \(a_i\) 发生的概率为 \(p(a_i)\),则它的信息量定义为:
\[ I(a_i) = \log_2 \frac{1}{p(a_i)} = -\log_2 p(a_i) \] -
熵 (Entropy): 对于一个有 \(n\) 个可能取值的离散随机变量 \(X\),其概率分布为 \(P(X=x_i) = p_i\),则 \(X\) 的熵定义为所有可能事件信息量的数学期望:
\[ H(X) = -\sum_{i=1}^{n} p_i \log_2 p_i \]这里的对数底数通常取 2,此时熵的单位是比特 (bit)。
熵的特性:
- 范围: 对于有 \(n\) 个取值的随机变量,其熵的范围是 \(0 \le H(X) \le \log_2 n\)。
- 最大熵: 当所有事件等概率发生时(即均匀分布
) ,系统不确定性最大,熵达到最大值 \(\log_2 n\)。 - 最小熵: 当某个事件的概率为 1,其余为 0 时(即确定性系统
) ,系统不确定性最小,熵为 0。
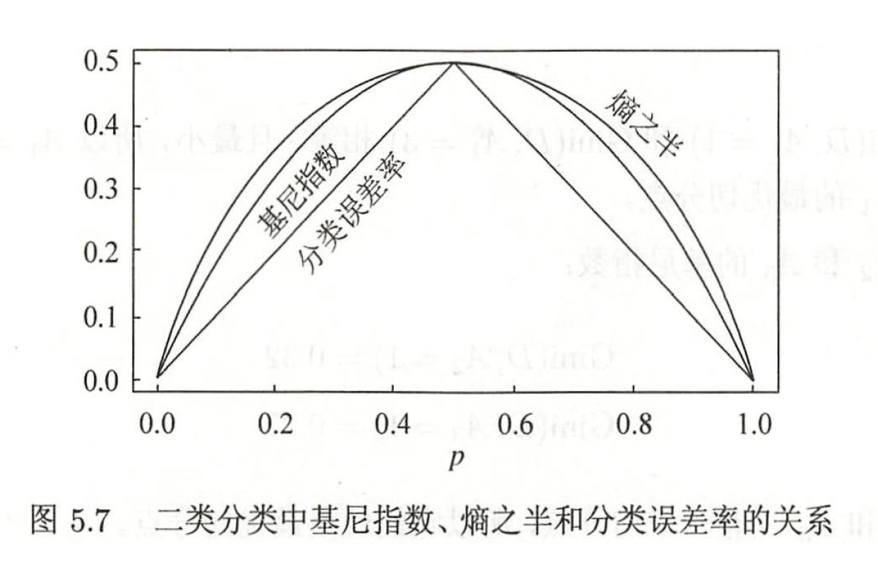
下图展示了二分类问题(伯努利分布)中,熵与概率 \(p\) 的关系。当 \(p=0.5\) 时,不确定性最大,熵达到峰值 1。
信息增益 (Information Gain) (page 28-29) ¶
信息增益表示在得知特征 A 的信息后,导致数据集 D 的类别不确定性减少的程度。不确定性的减少量越大,说明特征 A 的分类能力越强。
要计算信息增益,我们首先需要定义条件熵 (Conditional Entropy)。
条件熵与信息增益
-
条件熵 \(H(Y|X)\): 表示在已知随机变量
X的条件下,随机变量Y的不确定性。其计算公式为:\[ H(Y|X) = \sum_{i=1}^{n} p(X=x_i) H(Y|X=x_i) \]它是在
X取不同值的情况下Y的熵的加权平均。 -
信息增益 \(g(D, A)\): 定义为数据集
D的经验熵 \(H(D)\) 与在特征A给定条件下的经验条件熵 \(H(D|A)\) 之差:\[ g(D, A) = H(D) - H(D|A) \]
Note
- \(H(D)\) 度量了在不知道任何特征信息时,对数据集
D进行分类的不确定性。 - \(H(D|A)\) 度量了在知道了特征
A的取值后,对数据集D进行分类的剩余不确定性。 - 两者的差值 \(g(D, A)\) 就是特征
A为分类带来的信息量。ID3 算法在每一步都选择使信息增益最大的特征作为划分标准。 - 信息增益在信息论中也被称为互信息 (Mutual Information)。
信息增益的算法 (page 31-32) ¶
信息增益计算步骤
输入: 训练数据集 \(D\),特征 \(A\)。
输出: 特征 \(A\) 对数据集 \(D\) 的信息增益 \(g(D, A)\)。
-
计算数据集的经验熵 \(H(D)\) 假设数据集 \(D\) 有 \(K\) 个类别 \(C_k\), \(|C_k|\) 是属于第 \(k\) 类的样本数, \(|D|\) 是总样本数。
\[ H(D) = -\sum_{k=1}^{K} \frac{|C_k|}{|D|} \log_2 \frac{|C_k|}{|D|} \] -
计算特征 A 对数据集 D 的经验条件熵 \(H(D|A)\) 假设特征 \(A\) 有 \(n\) 个不同的取值 \(\{a_1, a_2, \dots, a_n\}\),根据这些取值将 \(D\) 划分为 \(n\) 个子集 \(\{D_1, D_2, \dots, D_n\}\)。\(|D_i|\) 是 \(A=a_i\) 的样本数。\(|D_{ik}|\) 是子集 \(D_i\) 中属于类别 \(C_k\) 的样本数。
\[ H(D|A) = \sum_{i=1}^{n} \frac{|D_i|}{|D|} H(D_i) = -\sum_{i=1}^{n} \frac{|D_i|}{|D|} \sum_{k=1}^{K} \frac{|D_{ik}|}{|D_i|} \log_2 \frac{|D_{ik}|}{|D_i|} \] -
计算信息增益
\[ g(D, A) = H(D) - H(D|A) \]
信息增益例题 (page 33-35) ¶
贷款申请数据
我们使用贷款申请样本数据表(共 15 个样本
目标:选择“年龄”
-
计算经验熵 \(H(D)\) 数据集中,9个样本被批准贷款(是),6个被拒绝(否)。
\[ H(D) = -\left( \frac{9}{15} \log_2 \frac{9}{15} + \frac{6}{15} \log_2 \frac{6}{15} \right) \approx 0.971 \] -
计算各特征的信息增益
-
A1: 年龄 ( 青年、中年、老年 )
- 青年 (5 个 ): 2 是 , 3 否 -> \(H(D_1) = 0.971\)
- 中年 (5 个 ): 3 是 , 2 否 -> \(H(D_2) = 0.971\)
- 老年 (5 个 ): 4 是 , 1 否 -> \(H(D_3) = 0.722\) \(g(D, A_1) = H(D) - \left[ \frac{5}{15}H(D_1) + \frac{5}{15}H(D_2) + \frac{5}{15}H(D_3) \right] \approx 0.083\)
-
A2: 有工作 ( 是、否 )
- 是 (5 个 ): 5 是 , 0 否 -> \(H(D_1) = 0\)
- 否 (10 个 ): 4 是 , 6 否 -> \(H(D_2) = 0.971\) \(g(D, A_2) = H(D) - \left[ \frac{5}{15}H(D_1) + \frac{10}{15}H(D_2) \right] \approx 0.324\)
-
A3: 有自己的房子 ( 是、否 )
- 是 (6 个 ): 6 是 , 0 否 -> \(H(D_1) = 0\)
- 否 (9 个 ): 3 是 , 6 否 -> \(H(D_2) = 0.918\) \(g(D, A_3) = H(D) - \left[ \frac{6}{15}H(D_1) + \frac{9}{15}H(D_2) \right] \approx 0.420\)
-
A4: 信贷情况 ( 一般、好、非常好 )
- 一般 (5 个 ): 1 是 , 4 否
- 好 (6 个 ): 4 是 , 2 否
- 非常好 (4 个 ): 4 是 , 0 否 \(g(D, A_4) = \dots \approx 0.363\)
-
-
比较信息增益 比较四个特征的信息增益值:\(g(D, A_3) > g(D, A_4) > g(D, A_2) > g(D, A_1)\)。
结论: 特征 A3 ( 有自己的房子 ) 的信息增益最大,因此 ID3 算法会选择它作为根结点进行划分。
信息增益比 (page 36) ¶
虽然信息增益是一个很好的度量,但它有一个固有的偏见:倾向于选择取值数目较多的特征。极端情况下,如果一个特征的每个取值都唯一对应一个样本(如“ID 号”
为了校正这个问题,C4.5 算法引入了信息增益比 (Information Gain Ratio)。
信息增益比
信息增益比 \(g_R(D, A)\) 定义为信息增益 \(g(D, A)\) 与特征 \(A\) 本身的熵(也称为固有值 (Intrinsic Value))\(H_A(D)\) 之比:
其中,\(H_A(D)\) 的计算方式为:
这里 \(n\) 是特征 \(A\) 的取值个数。特征 \(A\) 的取值越多,其熵 \(H_A(D)\) 通常也越大,这就对信息增益起到了惩罚作用,从而平衡了特征选择。
决策树的生成 (page 37-42) ¶
决策树的生成是一个递归调用特征选择和数据划分的过程。
ID3 算法的生成过程 (page 38-41) ¶
ID3 算法
输入: 训练数据集 \(D\),特征集 \(A\),阈值 \(\epsilon\)。 输出: 决策树 \(T\)。
- 若 \(D\) 中所有实例属于同一类 \(C_k\),则 \(T\) 为单结点树,类标记为 \(C_k\),返回 \(T\)。
- 若特征集 \(A\) 为空,则 \(T\) 为单结点树,类标记为 \(D\) 中实例数最多的类,返回 \(T\)。
- 否则,计算 \(A\) 中各特征对 \(D\) 的信息增益,选择信息增益最大的特征 \(A_g\)。
- 若 \(g(D, A_g) < \epsilon\) ( 信息增益小于阈值 ),则 \(T\) 为单结点树,类标记为 \(D\) 中实例数最多的类,返回 \(T\)。
- 否则,对 \(A_g\) 的每一个可能值 \(a_i\),将 \(D\) 分割为非空子集 \(D_i\)。以 \(D_i\) 中实例数最多的类作为标记,构建子结点。
- 对第 \(i\) 个子结点,以 \(D_i\) 为训练集,以 \(A - \{A_g\}\) 为特征集,递归调用步骤 1-5,得到子树 \(T_i\),返回 \(T_i\)。
C4.5 算法的生成过程 (page 42) ¶
C4.5 算法的生成过程与 ID3 非常相似,主要区别在于特征选择标准:
- 将步骤 3 中的“信息增益”替换为“信息增益比”。
C4.5 的策略
C4.5 并非总是选择信息增益比最大的特征。它通常采用一种启发式方法:先从候选特征中找出信息增益高于平均值的特征,再从这些特征中选择信息增益比最高的。这样做可以避免对取值数目较少的特征产生不公平。
决策树面临的问题 (page 43-46) ¶
过度拟合 (Overfitting) ¶
这是决策树乃至许多机器学习模型都需要面对的核心问题。
- 理想的决策树应该是叶子结点少、深度小,即模型简单且有效。但寻找全局最优的决策树是一个NP 难题。
- 决策树生成算法倾向于不断生长,直到能完美划分训练数据为止。这会导致树过于复杂,学习到了训练数据中的噪声和偶然性,从而在新的、未见过的数据上表现很差。
- 训练误差 (Training Error): 模型在训练数据上的误差。
- 泛化误差 (Generalization Error): 模型在未知数据上的期望误差。
- 过拟合的典型表现就是训练误差很低,但泛化误差很高。
为了解决过拟合,需要采用剪枝 (Pruning) 技术。
连续值处理 ¶
ID3 等算法原生只支持离散特征。当遇到连续值特征(如年龄、收入)时,C4.5 和 CART 等算法采用二元分割 (Binary Split) 的方法。
- 将该连续特征的所有取值进行排序。
- 遍历所有可能的分割点(通常是相邻两个取值的中点
) 。 - 对每个分割点,计算其信息增益(或基尼指数等
) ,将其视为一个二分问题(如 年龄 <= t 和 年龄 > t) 。 - 选择能使信息增益最大的那个分割点作为该特征的最佳划分点。
决策树的剪枝 (page 47-51) ¶
剪枝是决策树学习算法中对付“过拟合”的主要手段。其基本策略是通过极小化决策树整体的损失函数来实现。
损失函数 ¶
决策树的损失函数(或称代价函数)需要平衡模型的拟合优度和复杂度。
结点上的经验熵为:\(H_{t}(T) = -\sum_{k=1}^{K} \frac{N_{tk}}{N_{t}}\log \frac{N_{tk}}{N_{t}}\)
决策树损失函数
设树 \(T\) 的叶结点个数为 \(|T|\),叶结点 \(t\) 有 \(N_t\) 个样本,其经验熵为 \(H_t(T)\)。损失函数定义为:
也可以写作:
- \(C(T) = \sum_{t=1}^{|T|} N_t H_t(T)\) 代表模型的训练误差,反映了模型对训练数据的拟合程度。树越复杂,\(C(T)\) 越小。
- \(|T|\) 代表模型的复杂度。
- \(\alpha \ge 0\) 是一个超参数,用于权衡拟合度与复杂度。\(\alpha\) 越大,模型就越倾向于选择更简单的树(叶结点更少
) 。
正则化的极大似然估计
损失函数(结构风险)的最小化等价于正则化的极大似然估计(最大后验估计
剪枝过程 ¶
剪枝过程是一个自底向上的回缩过程。
- 首先生成一棵完整的决策树 \(T\)。
- 递归地从树的叶结点向上回缩。
- 考察任意一个内部结点,比较剪枝前(该结点和其子树存在)和剪枝后(该结点变成一个叶结点)的损失函数值。
- 设剪枝前的子树为 \(T_B\),剪枝后的结点为 \(T_A\)。
- 如果 \(C_\alpha(T_A) \le C_\alpha(T_B)\),则说明剪枝是值得的,可以减少模型复杂度且不会过多地增加误差,于是执行剪枝。
- 重复这个过程,直到无法继续回缩,得到损失函数最小的子树 \(T_\alpha\)。
CART (Classification and Regression Trees) (page 52)¶
CART 算法由 Breiman 等人在 1984 年提出,是目前应用最广泛的决策树算法之一,像 Scikit-learn 库中的决策树实现就是基于 CART 的优化版本。
CART 算法特点
- 二叉树结构: 无论是分类还是回归,CART 生成的都是二叉树。它每次只将当前结点的数据集一分为二。
- 回归树: 使用平方误差最小化准则进行特征选择。
- 分类树: 使用基尼指数 (Gini Index) 最小化准则进行特征选择。
- 剪枝: 采用一种名为“代价复杂度剪枝”(Cost-Complexity Pruning)的精巧策略。
CART- 回归树的生成 (page 55-57) ¶
假设我们有一个连续的目标变量 \(Y\)。CART 回归树的目标是将输入空间(特征空间)划分为 \(M\) 个区域 \(R_m\),并且在每个区域内给出一个恒定的预测值 \(c_m\)。
-
预测模型: $$ f(x) = \sum_{m=1}^{M} c_m I(x \in R_m) $$ 其中 \(I(\cdot)\) 是指示函数。
-
最优预测值: 在一个区域 \(R_m\) 内,使平方误差最小的预测值 \(c_m\) 是该区域内所有样本 \(y_i\) 值的平均值。 $$ \hat{c}_m = \text{ave}(y_i | x_i \in R_m) $$
-
如何划分: 寻找最优的切分变量 \(j\) 和切分点 \(s\),使得划分后的两个区域的平方误差之和最小。 $$ \min_{j,s} \left[ \min_{c_1} \sum_{x_i \in R_1(j,s)} (y_i - c_1)^2 + \min_{c_2} \sum_{x_i \in R_2(j,s)} (y_i - c_2)^2 \right] $$ 其中 \(R_1(j,s)=\{x|x^{(j)}\leq s\}\) 和 \(R_2(j,s)=\{x|x^{(j)}>s\}\) 。
最小二乘回归树生成算法
- 选择最优切分: 遍历所有特征 \(j\),再对每个特征的所有可能取值 \(s\) 进行扫描,找到使平方误差和最小的最优对 \((j^*, s^*)\)。
- 划分区域: 使用 \((j^*, s^*)\) 将当前区域划分为两个子区域。
- 确定输出值: 计算每个子区域的输出值(均值
) 。 - 递归: 对两个子区域递归调用步骤 1-3,直到满足停止条件(如叶结点样本数小于阈值
) 。 - 生成树: 将输入空间划分为 \(M\) 个区域,生成最终的回归树。
CART- 分类树的生成 (page 58-60) ¶
CART 分类树使用基尼指数 (Gini Index) 来代替熵作为衡量数据“不纯度”的指标。
基尼指数
-
概率分布的基尼指数: 对于有 \(K\) 个类别的概率分布 \(p = (p_1, \dots, p_K)\),其基尼指数为:
\[ \text{Gini}(p) = \sum_{k=1}^{K} p_k (1-p_k) = 1 - \sum_{k=1}^{K} p_k^2 \]基尼指数的直观含义是:从数据集中随机抽取两个样本,其类别标记不一致的概率。基尼指数越小,数据集的纯度越高。
-
数据集 D 的基尼指数:
\[ \text{Gini}(D) = 1 - \sum_{k=1}^{K} \left( \frac{|C_k|}{|D|} \right)^2 \] -
特征 A 划分下的基尼指数: 如果特征 \(A\) 的某个取值 \(a\) 将数据集 \(D\) 划分为 \(D_1\) 和 \(D_2\),则此次划分的基尼指数为:
\[ \text{Gini}(D, A) = \frac{|D_1|}{|D|} \text{Gini}(D_1) + \frac{|D_2|}{|D|} \text{Gini}(D_2) \]
CART 分类树生成算法
- 计算基尼指数: 对每个特征 \(A\) 的每个可能切分点 \(a\),计算将数据集 \(D\) 分为 \(D_1\) (A=a) 和 \(D_2\) (A!=a) 后的基尼指数 \(\text{Gini}(D, A)\)。
- 选择最优切分: 在所有可能的特征和切分点中,选择使基尼指数最小的组合作为最优切分。
- 分配数据: 将数据集分配到两个子结点中。
- 递归: 对两个子结点递归调用步骤 1-3,直到满足停止条件。
- 生成树: 生成最终的 CART 分类树。
CART 的剪枝 (page 66-73) ¶
CART 的剪枝策略非常系统化,分为两个步骤:
-
生成子树序列:
- 首先,生成一棵足够大的决策树 \(T_0\)。
- 然后,通过代价复杂度剪枝,生成一个嵌套的子树序列 \(\{T_0, T_1, \dots, T_n\}\)。这个序列是通过不断增加正则化参数 \(\alpha\) 得到的。
- 对于 \(T_0\) 中的每个内部结点 \(t\),计算一个“剪枝效用”指标 \(g(t)\): $$ g(t) = \frac{C(t) - C(T_t)}{|T_t| - 1} $$ 其中 \(C(t)\) 是将 \(t\) 作为叶结点的误差,\(C(T_t)\) 是以 \(t\) 为根的子树的误差,\(|T_t|\) 是子树 \(T_t\) 的叶结点数。\(g(t)\) 表示剪掉子树 \(T_t\) 后,整体误差率的增加程度与复杂度减少程度的比值。
- 在 \(T_0\) 中剪去 \(g(t)\) 最小的结点,得到 \(T_1\)。在 \(T_1\) 中再剪去 \(g(t)\) 最小的结点,得到 \(T_2\),如此往复,直到只剩下根结点。
-
交叉验证选择最优子树:
- 使用一个独立的验证集 (Validation Set)。
- 对子树序列中的每一棵树 \(T_k\),在验证集上计算其误差(如平方误差或基尼指数
) 。 - 选择在验证集上误差最小的那棵树作为最终的最优决策树 \(T_\alpha\)。
这种方法通过将剪枝过程和最优树选择分离开,有效地避免了使用同一份数据既剪枝又评估的陷阱,找到了在拟合度和复杂度之间达到最佳平衡的模型。
习题 ¶
习题 5.1 ¶
Question
根据表 5.1 所给的训练数据集,利用信息增益比(C4.5 算法)生成决策树。
| ID | 年龄 | 有工作 | 有自己的房子 | 信贷情况 | 类别 |
|---|---|---|---|---|---|
| 1 | 青年 | 否 | 否 | 一般 | 否 |
| 2 | 青年 | 否 | 否 | 好 | 否 |
| 3 | 青年 | 是 | 否 | 好 | 是 |
| 4 | 青年 | 是 | 是 | 一般 | 是 |
| 5 | 青年 | 否 | 否 | 一般 | 否 |
| 6 | 中年 | 否 | 否 | 一般 | 否 |
| 7 | 中年 | 否 | 否 | 好 | 否 |
| 8 | 中年 | 是 | 是 | 好 | 是 |
| 9 | 中年 | 否 | 是 | 非常好 | 是 |
| 10 | 中年 | 否 | 是 | 非常好 | 是 |
| 11 | 老年 | 否 | 是 | 非常好 | 是 |
| 12 | 老年 | 否 | 是 | 好 | 是 |
| 13 | 老年 | 是 | 否 | 好 | 是 |
| 14 | 老年 | 是 | 否 | 非常好 | 是 |
| 15 | 老年 | 否 | 否 | 一般 | 否 |
分别以 A1(年龄), A2(有工作), A3(有自己的房子), A4(信贷情况)代表 4 个特征 , 计算各特征对数据集 D 的信息增益比 , 有(保留 3 位小数
\((1)\ g_R(D, A_1) = \frac{g(D, A_1)}{H_{A_1}(D)} = \frac{0.083}{3*( - \frac{5}{15}log_2{\frac{5}{15}})} = 0.052\)
\((2)\ g_R(D, A_2) = \frac{g(D, A_2)}{H_{A_2}(D)} = \frac{0.324}{-\frac{5}{15}log_2{\frac{5}{15}} - \frac{10}{15}log_2{\frac{10}{15}}} = 0.353\)
\((3)\ g_R(D, A_3) = \frac{g(D, A_3)}{H_{A_3}(D)} = \frac{0.420}{-\frac{6}{15}log_2{\frac{6}{15}} - \frac{9}{15}log_2{\frac{9}{15}}} = 0.433\)
\((4)\ g_R(D, A_4) = \frac{g(D, A_4)}{H_{A_4}(D)} = \frac{0.363}{-\frac{5}{15}log_2{\frac{5}{15}} - \frac{6}{15}log_2{\frac{6}{15}} - \frac{4}{15}log_2{\frac{4}{15}}} = 0.232\)
由于特征 A3 ( 有自己的房子 ) 的信息增益比最大 , 所以选择特征 A3 作为根结点的特征。
它将训练集 D 划分为两个子集 D1 (A3 取值为 " 是 ") 和 D2 (A3 取值为 " 否 ")。由于 D1 只有同一类的样本点 , 所以它成为一个叶结点 , 结点的类标记为 " 是 "。对于 D2 则需从特征 A1 ( 年龄 ), A2 ( 有工作 ), A4 ( 信贷情况 ) 中选择新的特征。
计算各个特征的信息增益比 :
\(g_R(D_2, A_1) = \frac{g(D_2, A_1)}{H_{A_1}(D_2)} = \frac{0.251}{-\frac{4}{9}log_2{\frac{4}{9}} - \frac{2}{9}log_2{\frac{2}{9}} - \frac{3}{9}log_2{\frac{3}{9}}} = 0.164\)
\(g_R(D_2, A_2) = \frac{g(D_2, A_2)}{H_{A_2}(D_2)} = \frac{0.918}{-\frac{3}{9}log_2{\frac{3}{9}} - \frac{6}{9}log_2{\frac{6}{9}}} = 1.000\)
\(g_R(D_2, A_4) = \frac{g(D_2, A_4)}{H_{A_4}(D_2)} = \frac{0.474}{-\frac{4}{9}log_2{\frac{4}{9}} - \frac{4}{9}log_2{\frac{4}{9}} - \frac{1}{9}log_2{\frac{1}{9}}} = 0.340\)
选择信息增益比最大的特征 A2 ( 有工作 ) 作为结点的特征 , 从这一结点引出两个子结点 : 一个是对应 " 是 " ( 有工作 ) 的子结点 , 包含 3 个样本 , 它们属于同一类 , 所以这是一个叶结点 , 类标记为 " 是 "; 另一个是对应 " 否 " ( 无工作 ) 的子结点 , 包含 6 个样本 , 它们也属于同一类 , 所以这也是一个叶结点 , 类标记为 " 否 "。
这样生成一个如下图所示的决策树。该决策树只用了两个特征 ( 有两个内部节点 ):
graph LR
A[有自己的房子] -->|是| B(是)
A -->|否| C[有工作]
C -->|是| D(是)
C -->|否| E(否)习题 5.2 ¶
Question
已知如表 5.2 所示的训练数据,试用平方误差损失准则生成一个二叉回归树。
| \(x_{i}\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(y_i\) | 4.50 | 4.75 | 4.91 | 5.34 | 5.80 | 7.05 | 7.90 | 8.23 | 8.70 | 9.00 |
- 由数据表可知,j 只能取 1,选择最优切分点 s,遍历求解
| s | \(\sum_{x_i \in R_1(1, s)}(y_i - \hat{c}_1)^2 + \sum_{x_i \in R_2(1, s)}(y_i - \hat{c}_2)^2\) |
|---|---|
| 1 | 22.648 |
| 2 | 17.702 |
| ... | .. |
| 9 | 21.328 |
| 10 | 所有的点都在 \(R_1\) 内,则输入空间不变 |
- 则当 j = 1, s = 5 时取得最小值,将输入空间划分为两个区域 x <= 5 和 x > 5。
- 接着,对两个子区域按上述过程递归计算,设定阈值为 0.2(自调整
) ;后续过程比较繁琐,考虑使用 python 完成,结果为:
python 代码及运行结果 ¶
Env
- python=3.11.11
- numpy=2.1.2
import json
import numpy as np
class Node:
"""Tree node for least squares regression tree."""
def __init__(self, value, feature, left=None, right=None):
self.value = value.tolist() if isinstance(value, np.ndarray) else value
self.feature = feature.tolist() if isinstance(feature, np.ndarray) else feature
self.left = left
self.right = right
def __repr__(self):
"""Convert node to JSON string representation."""
def custom_default(obj):
if isinstance(obj, Node):
return obj.__dict__
# Handle numpy types by converting to Python standard types
if isinstance(
obj,(
np.int_,
np.intc,
np.intp,
np.int8,
np.int16,
np.int32,
np.int64,
np.uint8,
np.uint16,
np.uint32,
np.uint64,),
):
return int(obj)
if isinstance(obj, (np.float_, np.float16, np.float32, np.float64)):
return float(obj)
if isinstance(obj, np.ndarray):
return obj.tolist()
return str(obj)
return json.dumps(self, indent=3, default=custom_default, ensure_ascii=False)
class LeastSquareRegTree:
"""Least squares regression tree implementation."""
def __init__(self, train_X, train_y, epsilon=0.1, min_samples_split=2):
self.X = np.asarray(train_X)
self.y = np.asarray(train_y)
self.feature_count = self.X.shape[1]
self.epsilon = epsilon
self.min_samples_split = min_samples_split
self.tree = None
def _fit(self, X, y, feature_count):
j, s, min_error, c1, c2 = self._find_best_split(X, y, feature_count)
tree = Node(feature=j, value=X[s, j], left=None, right=None)
left_mask = X[:, j] <= X[s, j]
right_mask = ~left_mask
X_left, y_left = X[left_mask], y[left_mask]
X_right, y_right = X[right_mask], y[right_mask]
if min_error < self.epsilon or len(y_left) < self.min_samples_split:
tree.left = float(c1) # Convert numpy types to Python standard types
else:
tree.left = self._fit(X_left, y_left, feature_count)
if min_error < self.epsilon or len(y_right) < self.min_samples_split:
tree.right = float(c2) # Convert numpy types to Python standard types
else:
tree.right = self._fit(X_right, y_right, feature_count)
return tree
def fit(self):
self.tree = self._fit(self.X, self.y, self.feature_count)
return self
def predict(self, X):
if self.tree is None:
raise ValueError("tree is empty")
X = np.asarray(X)
predictions = np.zeros(X.shape[0])
for i, sample in enumerate(X):
predictions[i] = self._predict_sample(sample, self.tree)
return predictions
def _predict_sample(self, sample, node):
if not isinstance(node, Node):
return node
if sample[node.feature] <= node.value:
return self._predict_sample(sample, node.left)
else:
return self._predict_sample(sample, node.right)
# Implements equation 5.21 from the textbook to find the split that minimizes squared error.
def _find_best_split(self, X, y, feature_count):
n_samples = len(X)
min_error = np.inf
best_feature = 0
best_split = 0
best_c1 = best_c2 = 0
for feature_idx in range(feature_count):
sorted_idx = np.argsort(X[:, feature_idx])
sorted_X = X[sorted_idx]
sorted_y = y[sorted_idx]
unique_values = np.unique(sorted_X[:, feature_idx])
for i in range(len(unique_values) - 1):
split_value = (unique_values[i] + unique_values[i + 1]) / 2
split_idx = np.searchsorted(sorted_X[:, feature_idx], split_value)
if split_idx == 0 or split_idx == n_samples:
continue # Skip if split would result in empty partition
left_y = sorted_y[:split_idx]
right_y = sorted_y[split_idx:]
c1 = np.mean(left_y)
c2 = np.mean(right_y)
error = np.sum((left_y - c1) ** 2) + np.sum((right_y - c2) ** 2)
if error < min_error:
min_error = error
best_feature = feature_idx
best_split = sorted_idx[split_idx - 1] # Index in original array
best_c1 = c1
best_c2 = c2
return best_feature, best_split, min_error, best_c1, best_c2
def __repr__(self):
return str(self.tree)
train_X = np.array([[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]]).T
train_y = np.array([4.50, 4.75, 4.91, 5.34, 5.80, 7.05, 7.90, 8.23, 8.70, 9.00])
model = LeastSquareRegTree(train_X, train_y, epsilon=0.2)
model.fit()
print(model)
{
"value": 5,
"feature": 0,
"left": {
"value": 3,
"feature": 0,
"left": 4.72,
"right": 5.57
},
"right": {
"value": 7,
"feature": 0,
"left": {
"value": 6,
"feature": 0,
"left": 7.05,
"right": 7.9
},
"right": {
"value": 8,
"feature": 0,
"left": 8.23,
"right": 8.85
}
}
}
-
泛化能力 (Generalization Ability): 指的是机器学习模型在处理未曾见过的(即非训练集的)新数据时表现出的准确性。 ↩