8 Adaboost

Adaboost 的起源 (page 3-4) ¶

要理解 AdaBoost，我们首先需要追溯到计算学习理论中的一个重要概念。

强可学习与弱可学习 (page 3) ¶

1984 年，计算机科学家 Kearns 和 Valiant 提出了“强可学习”（Strongly Learnable）和“弱可学习”（Weakly Learnable）的概念。这两个概念是在概率近似正确（Probably Approximately Correct, PAC） 学习框架下定义的。

PAC 学习框架

PAC 学习理论是计算学习理论的基石，它试图从数学上描述机器学习的可能性和效率。一个 PAC 可学习的算法，是指该算法能够在多项式时间内，以很高的概率，学习到一个近似正确的模型。

Probably ( 概率 )：指算法有很大概率（例如，大于 $1-\delta$）成功。
Approximately Correct ( 近似正确 )：指算法学到的模型错误率很低（小于 $\epsilon$）。

强可学习：如果存在一个多项式时间的学习算法，能够学习到一个概念（或类别），并且最终模型的正确率非常高（即错误率 $\epsilon$ 是一个任意小的正数），那么这个概念就被称为强可学习的。
弱可学习：如果存在一个多项式时间的学习算法，能够学习到一个概念，但学习的正确率仅比随机猜测好一点（例如，对于二分类问题，正确率略高于 50%），那么这个概念就被称为弱可学习的。

核心问题的提出 (page 3-4) ¶

在很长一段时间里，人们都在寻找高效的强学习算法，但这通常非常困难。一个自然而然的问题是：弱可学习与强可学习是否等价？换句话说，我们能否将一个只能获得“比瞎猜好一点”的弱学习算法，提升（Boost）为一个正确率极高的强学习算法？

1989 年，Robert Schapire 给出了一个里程碑式的肯定回答。

Schapire 的证明

Schapire 证明：在 PAC 学习框架下，一个概念是强可学习的充分必要条件是这个概念是弱可学习的。

这个证明的意义是革命性的。它告诉我们，不必再苦苦追寻难以设计的强学习算法。我们只需要找到一个弱学习算法（这通常容易得多），然后通过某种方式将其“提升”为强学习算法即可。这直接催生了后来的 Boosting 系列算法。

怎样实现弱学习转为强学习 (page 5-7) ¶

既然理论上可行，那么实践中如何操作呢？核心思想是组合多个弱学习器。

例如，算法 A 在某些情况下表现不佳，而算法 B 在另外一些情况下表现不佳，但它们失效的场景可能并不重合。通过将它们以某种方式组合起来，就有可能实现“取长补短”，得到一个在各种情况下都表现良好的强学习器。

这引出了两个关键问题：

怎样获得不同的弱分类器？
怎样组合这些弱分类器？

如何获得不同的弱分类器 (page 6) ¶

要获得性能各异的弱学习器，有以下几种常见策略：

使用不同的学习算法：例如，一个弱学习器用逻辑回归，另一个用朴素贝叶斯。
使用相同算法但参数不同：例如，使用 K-Means 算法时选择不同的 K 值，或使用神经网络时设置不同的隐层结构。
使用不同的数据表示：对同一个输入对象，提取不同的特征集进行训练。
使用不同的训练集：这是最主流的方法，主要有两种技术：
- 装袋（Bagging）：通过自助采样（Bootstrap Sampling）从原始数据集中生成多个不同的训练子集，各个弱学习器之间并行训练，互不影响。
- 提升（Boosting）：所有弱学习器串行训练，后一个学习器会重点关注前一个学习器分错的样本。AdaBoost 就是 Boosting 的代表。

Adaboost 的提出 (page 7) ¶

基于 Boosting 的思想，一系列算法被提出：

1990 年：Schapire 构造出第一个多项式级的 Boosting 算法。
1993 年：Drunker 和 Schapire 首次将神经网络作为弱学习器，应用 Boosting 算法解决光学字符识别（OCR）问题。
1995 年：Freund 和 Schapire 提出了 AdaBoost (Adaptive Boosting) 算法。AdaBoost 在效率上与早期 Boosting 算法相当，但其巨大优势在于它不需要任何关于弱学习器性能的先验知识，非常易于应用到实际问题中，因此迅速成为最流行和最成功的 Boosting 算法之一。

Adaboost 基本概念 (page 8-11) ¶

AdaBoost 的全称是 Adaptive Boosting，即“自适应提升”。它的核心思想可以概括为：“从多个弱者中建立一个强者” (Building a strong classifier from a lot of weaker ones)。

核心思想 (page 9-10) ¶

假设我们有一系列的弱分类器 $h_1(x), h_2(x), \dots, h_T(x)$，每个分类器的输出为 $\{-1, +1\}$。AdaBoost 将它们组合成一个强分类器 $H_T(x)$ 的方式是加权投票：

\[ H_T(x) = \text{sign} \left( \sum_{t=1}^{T} \alpha_t h_t(x) \right) \]

其中，$\alpha_t$ 是第 $t$ 个弱分类器的权重。

那么，之前提出的两个问题在 AdaBoost 中是如何解决的呢？

如何获得不同的弱分类器？( 每一轮如何改变训练数据的权值或概率分布？)
- AdaBoost 在每一轮训练中，会提高那些被前一轮弱分类器错误分类样本的权重，降低那些被正确分类样本的权重。这样，后续的弱分类器就会更加关注那些“难啃的骨头”。
如何组合弱分类器？
- AdaBoost 采用加权多数表决。对于分类误差率小的弱分类器，赋予其较大的权重 $\alpha_t$，使其在最终投票中起更大的作用；反之，对于分类误差率大的弱分类器，赋予其较小的权重，使其作用减小。

流程图示 (page 11) ¶

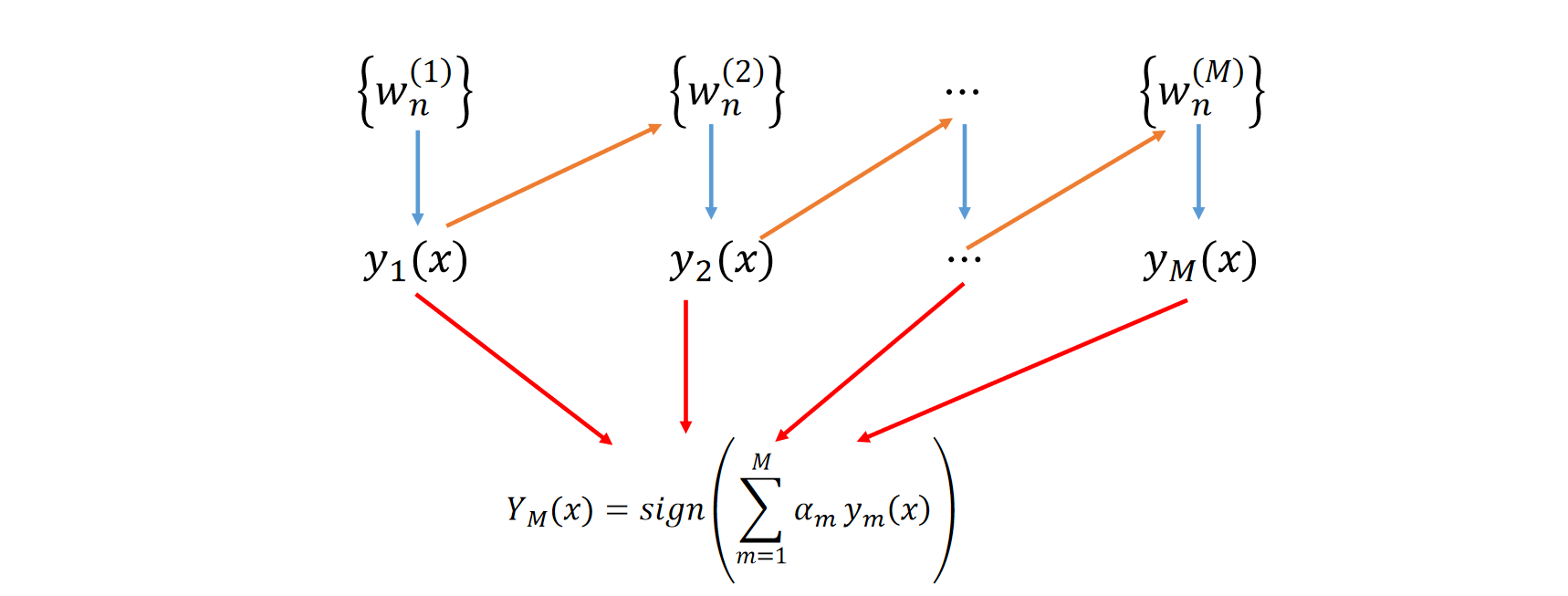
下图直观地展示了 AdaBoost 的流程：

初始时，所有样本有相同的权重 $\{w_n^{(1)}\}$。
在第一轮，基于权重 $\{w_n^{(1)}\}$ 训练出弱分类器 $y_1(x)$。
根据 $y_1(x)$ 的分类结果，更新样本权重得到 $\{w_n^{(2)}\}$（图中橙色箭头），分错的样本权重会增加。
在第二轮，基于新的权重 $\{w_n^{(2)}\}$ 训练出弱分类器 $y_2(x)$。
... 这个过程重复 M 轮，得到 M 个弱分类器和它们各自的权重 $\alpha_m$。
最终分类器 $Y_M(x)$ 是这 M 个弱分类器的加权组合。

AdaBoost 算法 (page 12-14) ¶

下面我们来详细描述 AdaBoost 算法的具体步骤。

AdaBoost 算法

输入：

训练数据集 $T = \{(x_1, y_1), (x_2, y_2), \dots, (x_N, y_N)\}$，其中 $x_i \in \mathcal{X} \subseteq \mathbb{R}^n$, $y_i \in \{-1, +1\}$。
弱学习算法。

输出：最终分类器 $G(x)$。

算法步骤：

初始化训练数据的权值分布

\[ D_1 = (w_{11}, \dots, w_{1i}, \dots, w_{1N}), \quad w_{1i} = \frac{1}{N}, \quad i=1, 2, \dots, N \]
对 $m = 1, 2, \dots, M$ 进行迭代

a. 使用带有权值分布 $D_m$ 的训练数据集学习，得到弱分类器 $G_m(x): \mathcal{X} \to \{-1, +1\}$。

b. 计算 $G_m(x)$ 在训练数据集上的加权误差率 $e_m$：

\[ e_m = P(G_m(x_i) \neq y_i) = \sum_{i=1}^{N} w_{mi} I(G_m(x_i) \neq y_i) \]

c. 计算 $G_m(x)$ 的系数 $\alpha_m$ ( 即分类器权重 )：

$$ \alpha_m = \frac{1}{2} \log \frac{1-e_m}{e_m} $$

d. 更新训练数据集的权值分布 $D_{m+1}$：

\[ \begin{align} w_{m+1, i} &= \frac{w_{mi}}{Z_m} \exp(-\alpha_m y_i G_m(x_i)) \\ \text{其中 } Z_m &= \sum_{i=1}^{N} w_{mi} \exp(-\alpha_m y_i G_m(x_i)) \text{ 是规范化因子} \end{align} \]
构建最终分类器

将各轮得到的弱分类器加权组合：

\[ f(x) = \sum_{m=1}^{M} \alpha_m G_m(x) \]

得到最终分类器：

\[ G(x) = \text{sign}(f(x)) = \text{sign} \left( \sum_{m=1}^{M} \alpha_m G_m(x) \right) \]

算法说明 (page 15) ¶

我们来仔细分析一下算法中的几个关键公式：

分类器权重 $\alpha_m$：

\[ \alpha_m = \frac{1}{2} \log \frac{1-e_m}{e_m} \]

这个公式的性质是，当加权误差率 $e_m \le \frac{1}{2}$ 时，$\alpha_m \ge 0$。并且 $e_m$ 越小，$\alpha_m$ 越大。这符合我们的直觉：分类效果越好的弱分类器，在最终投票中的话语权越大。如果一个弱分类器效果比随机猜测还差（$e_m > 0.5$），它的权重就会是负数。
样本权重更新 $w_{m+1, i}$：

注意到 $y_i G_m(x_i)$ 的取值： - 如果样本 $x_i$ 被正确分类，则 $y_i G_m(x_i) = 1$。 - 如果样本 $x_i$ 被错误分类，则 $y_i G_m(x_i) = -1$。

因此，权重更新公式可以写成：

\[ w_{m+1, i} = \begin{cases} \frac{w_{mi}}{Z_m} e^{-\alpha_m}, & \text{若 } G_m(x_i) = y_i \text{ (分类正确)} \\ \frac{w_{mi}}{Z_m} e^{\alpha_m}, & \text{若 } G_m(x_i) \neq y_i \text{ (分类错误)} \end{cases} \]

这意味着，被错误分类的样本，其权值将被放大 $e^{\alpha_m}$ 倍；被正确分类的样本，其权值将被缩小 $e^{-\alpha_m}$ 倍。

我们可以进一步计算误分类样本权值的放大倍数：

\[ e^{2\alpha_m} = e^{\log \frac{1-e_m}{e_m}} = \frac{1-e_m}{e_m} \]

这说明，一个弱分类器的误差率越低，那些被它分错的样本在下一轮的权重就会被放大得越多。

Boosting 图示 (page 16-21) ¶

这组图片生动地展示了 AdaBoost 的过程：

初始状态：数据点有相同的权重。第一个弱分类器Weak Classifier 1 ( 虚线 ) 尝试对数据进行划分，但分错了三个点（两个蓝点，一个红点）。
权重更新：这三个被分错的点，它们的权重被增大了（图中圆圈变大）。
第二轮训练：Weak Classifier 2 在新的权重下进行训练。由于之前分错的点权重更大，这个分类器会更倾向于把它们分对。
再次更新权重：Classifier 2 也分错了一些点，这些点的权重又被增大。
第三轮训练：Weak Classifier 3 针对最新的权重分布进行学习。
最终组合：将三个弱分类器根据它们的 $\alpha$ 权重进行组合，得到一个更复杂的、非线性的决策边界，它能够正确地划分所有数据点。

例子 (page 22-25) ¶

让我们通过一个具体的例子来演算 AdaBoost 的过程。

AdaBoost 计算实例

给定数据：

序号	1	2	3	4	5	6	7	8	9	10
x	0	1	2	3	4	5	6	7	8	9
y	1	1	1	-1	-1	-1	1	1	1	-1

弱分类器：由阈值 $v$ 产生的决策树桩（Decision Stump）¹，形式为 $x < v$ 或 $x > v$。

m = 1 ( 第一轮 )

初始化权重：$D_1 = (0.1, 0.1, \dots, 0.1)$。
寻找最佳弱分类器 $G_1(x)$：在 $D_1$ 权重下，我们尝试不同的阈值 $v$。可以发现，当 $v=2.5$ 时，弱分类器 $G_1(x) = \begin{cases} 1, & x < 2.5 \\ -1, & x > 2.5 \end{cases}$ 的加权误差率最小。此时，样本 6, 7, 8 (x=5, 6, 7) 被分错。
计算误差率 $e_1$： $e_1 = P(G_1(x_i) \neq y_i) = w_{1,6} + w_{1,7} + w_{1,8} = 0.1 + 0.1 + 0.1 = 0.3$。
计算分类器权重 $\alpha_1$： $\alpha_1 = \frac{1}{2} \log \frac{1-e_1}{e_1} = \frac{1}{2} \log \frac{0.7}{0.3} \approx 0.4236$。
更新样本权重 $D_2$：
- 分类正确的样本 (1-5, 9, 10)，新权重为 $\frac{0.1}{Z_1}e^{-0.4236}$。
- 分类错误的样本 (6-8)，新权重为 $\frac{0.1}{Z_1}e^{0.4236}$。
- 计算归一化因子 $Z_1 = 7 \times 0.1 \times e^{-0.4236} + 3 \times 0.1 \times e^{0.4236} \approx 0.9167$。
- 可得 $D_2 \approx (0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.1666, 0.1666, 0.1666, 0.0715, 0.1666)$。

m = 2 ( 第二轮 )

寻找最佳弱分类器 $G_2(x)$：在 $D_2$ 权重下，我们再次寻找最佳阈值。此时，样本 6,7,8 的权重很高。可以发现，当 $v=8.5$ 时，弱分类器 $G_2(x) = \begin{cases} 1, & x < 8.5 \\ -1, & x > 8.5 \end{cases}$ 的加权误差率最小。此时，样本 4, 5, 6 (x=3, 4, 5) 被分错。
计算误差率 $e_2$： $e_2 = w_{2,4} + w_{2,5} + w_{2,6} = 0.0715 \times 3 \approx 0.2143$。
计算分类器权重 $\alpha_2$： $\alpha_2 = \frac{1}{2} \log \frac{1-0.2143}{0.2143} \approx 0.6496$。
更新样本权重 $D_3$ ...

m = 3 ( 第三轮 )

寻找最佳弱分类器 $G_3(x)$：在 $D_3$ 权重下，当 $v=5.5$ 时，弱分类器 $G_3(x) = \begin{cases} -1, & x < 5.5 \\ 1, & x > 5.5 \end{cases}$ 的加权误差率最小。此时，样本 1, 2, 3, 10 (x=0, 1, 2, 9) 被分错。
计算误差率 $e_3$： $e_3 \approx 0.1820$。
计算分类器权重 $\alpha_3$： $\alpha_3 \approx 0.7514$。

最终分类器

经过三轮，我们得到的最终分类器为：

\[ G(x) = \text{sign}[f_3(x)] = \text{sign}[0.4236G_1(x) + 0.6496G_2(x) + 0.7514G_3(x)] \]

将所有数据点代入上式，可以发现 $f_3(x)$ 的符号与真实标签 $y$ 完全一致，误分类点为 0。我们成功地将三个各有错误的弱分类器组合成了一个完美的强分类器。

AdaBoost 的训练误差分析 (page 26-29) ¶

AdaBoost 一个美妙的性质是，它的训练误差会随着迭代次数的增加呈指数级下降。

AdaBoost 训练误差界

AdaBoost 算法最终分类器的训练误差界为：

\[ \frac{1}{N} \sum_{i=1}^{N} I(G(x_i) \neq y_i) \le \frac{1}{N} \sum_{i=1}^{N} \exp(-y_i f(x_i)) = \prod_{m=1}^{M} Z_m \]

证明思路 (page 27) ¶

第一个不等式: $I(G(x_i) \neq y_i) \le \exp(-y_i f(x_i))$。
- 当 $G(x_i) = y_i$ 时， $y_i f(x_i) > 0$，不等式左边为 0，右边为正数，成立。
- 当 $G(x_i) \neq y_i$ 时， $y_i f(x_i) \le 0$，不等式左边为 1，右边 $\exp(-y_i f(x_i)) \ge e^0 = 1$，成立。
第二个等式: $\frac{1}{N} \sum \exp(-y_i f(x_i)) = \prod Z_m$。
- 这个等式可以通过递推关系证明。核心是利用 $f_m(x) = f_{m-1}(x) + \alpha_m G_m(x)$ 和权重更新公式 $w_{m+1,i} = \frac{w_{mi}}{Z_m} \exp(-\alpha_m y_i G_m(x_i))$。通过展开，可以发现每一轮迭代都会乘上一个 $Z_m$ 因子。

这个定理告诉我们，要想让训练误差小，就要让 $\prod Z_m$ 尽可能小。接下来我们分析单个 $Z_m$。

规范化因子 $Z_m$ 的上界

\[ Z_m = \sum_{i=1}^{N} w_{mi} \exp(-\alpha_m y_i G_m(x_i)) = 2\sqrt{e_m(1-e_m)} \]

引入 $\gamma_m = \frac{1}{2} - e_m$，这个值衡量了弱分类器的性能比随机猜测好多少。那么上式可以写为：

\[ Z_m = \sqrt{1 - 4\gamma_m^2} \le \exp(-2\gamma_m^2) \]

证明思路 (page 28) ¶

通过对 $Z_m$ 关于 $\alpha_m$ 求导并令其为 0，可以证明 AdaBoost 算法中选择的 $\alpha_m = \frac{1}{2}\log\frac{1-e_m}{e_m}$ 恰好是使 $Z_m$ 最小化的选择。将此 $\alpha_m$ 代入 $Z_m$ 的表达式即可得到等式。最后利用不等式 $1-t \le e^{-t}$ ( 当 $t \ge 0$)，可得到最终的不等式界。

误差指数下降 (page 29) ¶

结合以上两个定理，我们可以得到最终的结论：

\[ \frac{1}{N} \sum_{i=1}^{N} I(G(x_i) \neq y_i) \le \prod_{m=1}^{M} Z_m \le \prod_{m=1}^{M} \exp(-2\gamma_m^2) = \exp\left(-2\sum_{m=1}^{M}\gamma_m^2\right) \]

训练误差指数下降

如果存在 $\gamma > 0$，对所有 $m$ 都有 $\gamma_m \ge \gamma$（即每个弱分类器都比随机猜测好一个固定的量），则：

\[ \frac{1}{N} \sum_{i=1}^{N} I(G(x_i) \neq y_i) \le \exp(-2M\gamma^2) \]

这个结果表明，AdaBoost 的训练误差随着迭代次数 M 的增加，以指数速率下降。

AdaBoost 的“自适应性”

注意，在整个算法和推导中，我们并不需要预先知道弱分类器的性能下界 $\gamma$。算法能够自动适应每个弱分类器 $G_m$ 各自的训练误差率 $e_m$，并据此赋予其最优的权重 $\alpha_m$。这正是 AdaBoost 名字中 Adaptive（自适应） 的由来。

AdaBoost 算法的解释 (page 30) ¶

AdaBoost 算法还有另一种更具一般性的解释，可以将其看作是前向分步算法的一个特例。

AdaBoost 的另一种视角

模型：加法模型 (Additive Model)
损失函数：指数损失函数 (Exponential Loss Function)
学习算法：前向分步算法 (Forward Stagewise Algorithm)

前向分步算法 (page 31-33) ¶

首先我们来了解什么是加法模型。加法模型是指一个复杂的模型 $f(x)$ 可以表示为一系列基函数（basis function）$b(x; \gamma_m)$ 的线性组合：

\[ f(x) = \sum_{m=1}^{M} \beta_m b(x; \gamma_m) \]

在 AdaBoost 中，基函数就是弱分类器 $G_m(x)$，$\beta_m$ 是其权重 $\alpha_m$。

学习这样的模型，需要同时优化所有的参数 $\{\beta_m, \gamma_m\}_{m=1}^M$，这是一个非常复杂的优化问题。

\[ \min_{\beta_m, \gamma_m} \sum_{i=1}^{N} L \left( y_i, \sum_{m=1}^{M} \beta_m b(x_i; \gamma_m) \right) \]

前向分步算法 (Forward Stagewise Algorithm) 提供了一种贪心（greedy）的求解策略。它不是一次性优化所有参数，而是一步一步、从前向后地进行优化。在第 $m$ 步，它固定住前 $m-1$ 步得到的模型 $f_{m-1}(x)$，只求解当前步的基函数及其系数：

\[ (\beta_m, \gamma_m) = \arg\min_{\beta, \gamma} \sum_{i=1}^{N} L(y_i, f_{m-1}(x_i) + \beta b(x_i; \gamma)) \]

然后更新模型 $f_m(x) = f_{m-1}(x) + \beta_m b(x; \gamma_m)$。

前向分步算法

输入：训练数据 $T$，损失函数 $L(y, f(x))$，基函数集 $\{b(x;\gamma)\}$。输出：加法模型 $f(x)$。

初始化 $f_0(x) = 0$。
对 $m=1, 2, \dots, M$: a. 极小化损失函数，求解当前轮最优参数：

\[ (\beta_m, \gamma_m) = \arg\min_{\beta, \gamma} \sum_{i=1}^{N} L(y_i, f_{m-1}(x_i) + \beta b(x_i; \gamma)) \]

b. 更新模型：

\[ f_m(x) = f_{m-1}(x) + \beta_m b(x; \gamma_m) \]
得到最终加法模型 $f(x) = f_M(x) = \sum_{m=1}^M \beta_m b(x; \gamma_m)$。

AdaBoost 与前向分步算法的关系 (page 34-38) ¶

AdaBoost 是前向分步算法的特例

当 AdaBoost 的基分类器是二类分类器，并且损失函数为指数损失函数时，AdaBoost 算法等价于前向分步算法。

指数损失函数 (Exponential Loss Function) 定义为：

\[ L(y, f(x)) = \exp[-y f(x)] \]

证明 ¶

我们要证明的是，在前向分步算法框架下，如果使用指数损失，每一步求解最优的 $\alpha_m$ 和 $G_m(x)$，得到的结果与 AdaBoost 算法完全一致。

在第 $m$ 步，我们的目标是求解：

\[ (\alpha_m, G_m) = \arg\min_{\alpha, G} \sum_{i=1}^{N} \exp[-y_i(f_{m-1}(x_i) + \alpha G(x_i))] \]

我们可以把式子中的 $\exp[-y_i f_{m-1}(x_i)]$ 提出来，它在前一步已经确定，可以看作是第 $i$ 个样本的固定权重 $\bar{w}_{mi}$。

\[ (\alpha_m, G_m) = \arg\min_{\alpha, G} \sum_{i=1}^{N} \bar{w}_{mi} \exp[-y_i \alpha G(x_i)] \]

其中 $\bar{w}_{mi} = \exp[-y_i f_{m-1}(x_i)]$。

这个优化问题可以分两步求解：

求 $G_m^*(x)$：对于任意固定的 $\alpha > 0$，要使上式最小，就是要让 $\sum \bar{w}_{mi} I(y_i \neq G(x_i))$ 最小。这等价于在 $\bar{w}_{mi}$ 权重下，寻找一个误差率最小的弱分类器 $G(x)$。这和 AdaBoost 算法的步骤 2.a 完全一样。
求 $\alpha_m^*$：将求得的 $G_m^*(x)$ 代入，然后对 $\alpha$ 求导使其为 0。经过推导可以得到：

\[ \alpha_m^* = \frac{1}{2} \log \frac{1-e_m}{e_m} \]

其中 $e_m = \frac{\sum \bar{w}_{mi} I(y_i \neq G_m^*(x_i))}{\sum \bar{w}_{mi}}$ 是加权误差率。这和 AdaBoost 算法的步骤 2.c 完全一样。
更新权重：在前向分步算法中，下一轮的样本权重 $\bar{w}_{m+1,i}$ 由 $f_m(x)$ 决定：

\[ \bar{w}_{m+1,i} = \exp[-y_i f_m(x_i)] = \exp[-y_i(f_{m-1}(x_i)+\alpha_m G_m(x_i))] = \bar{w}_{mi}\exp[-y_i \alpha_m G_m(x_i)] \]

这与 AdaBoost 的权重更新规则（步骤 2.d）只相差一个规范化因子 $Z_m$，因此是等价的。

综上，AdaBoost 可以被严谨地解释为一个基于加法模型和指数损失的前向分步优化算法。

提升树 (Boosting Tree) (page 39-41) ¶

提升树是以决策树为基学习器的提升方法，是统计学习中性能最好的方法之一。

模型：提升树同样采用加法模型和前向分步算法。
基函数：基函数是决策树 $T(x; \Theta_m)$，其中 $\Theta_m$ 是决策树的参数（如划分点、叶节点值等）。
- 对于分类问题，是二叉分类树。
- 对于回归问题，是二叉回归树。
模型形式：

\[ f_M(x) = \sum_{m=1}^M T(x; \Theta_m) \]

提升树算法 (page 40-41) ¶

提升树的算法流程与前向分步算法一致，关键在于每一步如何确定下一棵树的参数 $\Theta_m$。

\[ \hat{\Theta}_m = \arg\min_{\Theta_m} \sum_{i=1}^N L(y_i, f_{m-1}(x_i) + T(x_i; \Theta_m)) \]

针对不同问题，使用不同的损失函数：

回归问题：常用平方误差损失。
分类问题：常用指数损失。
一般决策问题：可用其他一般损失函数。

提升树与 AdaBoost 的关系

对于二类分类问题，如果提升树算法使用指数损失函数，并且基学习器限制为决策树桩，那么该提升树算法就等价于 AdaBoost 算法。

回归问题的提升树算法 (page 42-48) ¶

我们来具体看一下当损失函数为平方误差时，提升树是如何工作的。

平方损失函数：$L(y, f(x)) = (y-f(x))^2$

在第 $m$ 步，我们需要求解：

\[ \hat{\Theta}_m = \arg\min_{\Theta_m} \sum_{i=1}^N (y_i - f_{m-1}(x_i) - T(x_i; \Theta_m))^2 \]

令 $r_{mi} = y_i - f_{m-1}(x_i)$，这个值被称为残差（Residual）。它是真实值与当前模型预测值之间的差距。于是，优化目标变为：

\[ \hat{\Theta}_m = \arg\min_{\Theta_m} \sum_{i=1}^N (r_{mi} - T(x_i; \Theta_m))^2 \]

这个式子的含义是：我们只需要用一棵新的决策树 $T(x; \Theta_m)$ 去拟合上一轮的残差 $r_{mi}$ 即可。

回归提升树算法

输入：训练数据 $T$。输出：提升树 $f_M(x)$。

初始化 $f_0(x) = 0$。
对 $m=1, 2, \dots, M$: a. 计算残差： $r_{mi} = y_i - f_{m-1}(x_i), \quad i=1, \dots, N$。 b. 将残差 $r_{mi}$ 作为新的训练标签，学习一棵回归树 $T(x; \hat{\Theta}_m)$，即用 $\{(x_i, r_{mi})\}_{i=1}^N$ 训练一棵树。 c. 更新模型： $f_m(x) = f_{m-1}(x) + T(x; \hat{\Theta}_m)$。
得到最终回归提升树 $f_M(x) = \sum_{m=1}^M T(x; \hat{\Theta}_m)$。

回归提升树实例 (page 45-48) ¶

PPT 中给出了一个详细的回归提升树计算例子。其核心步骤就是： 1. 第一步 (m=1)：$f_0(x)=0$，残差就是原始的 $y_i$。训练第一棵树 $T_1(x)$ 去拟合 $y_i$。得到 $f_1(x) = T_1(x)$。 2. 第二步 (m=2)：计算新残差 $r_{2i} = y_i - f_1(x_i)$。训练第二棵树 $T_2(x)$ 去拟合这些新残差。得到 $f_2(x) = f_1(x) + T_2(x)$。 3. 以此类推，每一轮都学习一棵树来修正上一轮的预测偏差。随着树的不断加入，模型的总平方误差（Loss）会持续下降。

梯度提升 (Gradient Boosting) (page 49-50) ¶

我们看到，当损失函数是平方损失时，提升树的优化非常直观，就是拟合残差。但对于一般的损失函数（如绝对值损失、Huber 损失等），优化就不再那么简单。

梯度提升（Gradient Boosting） 是由 Friedman 提出的一个更具一般性的框架。它的核心思想是：利用最速下降法的近似，将每一步的优化目标统一为拟合损失函数的负梯度。

损失函数 $L(y, f(x_i))$ 在当前模型 $f_{m-1}(x_i)$ 处的负梯度为：

\[ r_{mi} = - \left[ \frac{\partial L(y_i, f(x_i))}{\partial f(x_i)} \right]_{f(x) = f_{m-1}(x)} \]

梯度提升算法用这个负梯度值作为回归问题提升树中残差的近似值。

梯度与残差的关系

当损失函数为平方损失 $L(y, f) = \frac{1}{2}(y-f)^2$ 时，其负梯度为：

\[ -\frac{\partial L}{\partial f} = -(f-y) = y-f \]

这恰好就是残差！所以，我们之前讨论的回归提升树算法，是梯度提升算法在损失函数为平方损失时的一个特例。

梯度提升算法

输入：训练数据 $T$，损失函数 $L(y, f(x))$。输出：提升树 $\hat{f}(x)$。

初始化模型，使其损失最小。通常是一个常数值：

\[ f_0(x) = \arg\min_c \sum_{i=1}^N L(y_i, c) \]
对 $m=1, 2, \dots, M$: a. 对每个样本 $i=1, \dots, N$，计算负梯度（伪残差）：

$$ r_{mi} = - \left[ \frac{\partial L(y_i, f(x_i))}{\partial f(x_i)} \right]{f(x) = f $$}(x)

b. 用一棵回归树去拟合伪残差 $r_{mi}$，得到第 $m$ 棵树的叶节点区域 $R_{mj}, j=1, \dots, J$。 c. 对每个叶节点区域 $j=1, \dots, J$，计算最优的叶节点输出值 $c_{mj}$，以使损失最小：

$$ c_{mj} = \arg\min_c \sum_{x_i \in R_{mj}} L(y_i, f_{m-1}(x_i) + c) $$

d. 更新模型：

$$ f_m(x) = f_{m-1}(x) + \sum_{j=1}^J c_{mj} I(x \in R_{mj}) $$
得到最终模型 $\hat{f}(x) = f_M(x)$。

梯度提升算法将 AdaBoost、回归提升树等统一到了一个框架下，并可以推广到任意可微的损失函数，是目前应用最广泛、效果最好的机器学习算法之一，像 XGBoost、LightGBM 等都是其高效实现。

习题 ¶

习题 8.2 比较支持向量机、 AdaBoost 、逻辑斯谛回归模型的学习策略与算法。

结合所学，可以总结：

支持向量机
- 学习策略：软间隔最大化、最小化由合页损失函数和正则化项组成的目标函数
- 学习算法：凸二次规划、SMO 算法（序列最小最优化算法）
AdaBoost
- 学习策略：极小化通过加法模型组成的指数损失函数
- 学习算法：学习加法模型的前向分步算法
逻辑斯蒂回归模型
- 学习策略：极大似然估计法
- 学习算法：梯度下降法、牛顿法或拟牛顿法、改进的迭代尺度法

	学习策略	算法
支持向量机	软间隔最大化、最小化由合页损失函数和正则化项组成的目标函数	凸二次规划、SMO 算法（序列最小最优化算法）
AdaBoost	极小化通过加法模型组成的指数损失函数	学习加法模型的前向分步算法
逻辑斯谛回归	极大似然估计法	改进的迭代尺度法、梯度下降法、牛顿法或拟牛顿法

决策树桩 (Decision Stump): 一种最简单的决策树，只有一个决策节点和两个叶子节点。它基于单个特征的阈值进行划分。 ↩