9 Expect Max

EM（Expectation-Maximization，期望最大化）算法是一种在机器学习中应用广泛的迭代算法。它主要用于解决含有隐变量（latent variable）的概率模型的参数估计问题。当模型中存在无法直接观测到的变量时，我们无法像往常一样直接使用极大似然估计法（MLE）或极大后验概率估计法（MAP）。EM 算法通过一个巧妙的迭代过程，逐步优化模型参数，最终得到一个（局部）最优解。

EM 算法的引入 (page 2) ¶

EM 算法 (page 3) ¶

EM 算法的导出 (page 4-10) ¶

为了理解 EM 算法为何有效，我们需要深入其数学推导过程。这个过程巧妙地利用了 Jensen 不等式来寻找对数似然函数的一个下界，并通过最大化这个下界来逐步提升对数似然函数的值。

目标与困难 (page 4-5) ¶

假设我们有观测数据 \(Y\) 和隐变量数据 \(Z\)。\(Y\) 和 \(Z\) 一起构成了完全数据 (complete-data)。然而在现实中，我们通常只能得到 \(Y\)，即不完全数据 (incomplete-data)。

我们的目标是极大化观测数据 \(Y\) 的对数似然函数 \(L(\theta)\)：

这里，\(P(Y,Z|\theta)\) 是完全数据的联合概率分布，可以通过 \(P(Y,Z|\theta) = P(Y|Z,\theta)P(Z|\theta)\) 计算。

构造下界 (page 6-8) ¶

EM 算法不直接最大化 \(L(\theta)\)，而是通过最大化它的一个下界 (lower bound) 来间接实现。假设在第 \(i\) 次迭代后，我们得到的参数估计是 \(\theta^{(i)}\)。我们希望找到一个新的参数 \(\theta\)，使得 \(L(\theta) > L(\theta^{(i)})\)。

考虑二者之差 \(L(\theta) - L(\theta^{(i)})\)：

这里我们引入一个关于隐变量 \(Z\) 的分布 \(P(Z|Y, \theta^{(i)})\)，并利用Jensen 不等式³ 进行放缩：

整理上式，我们可以得到 \(L(\theta)\) 的一个下界函数 \(B(\theta, \theta^{(i)})\)：

我们希望通过最大化这个下界 \(B(\theta, \theta^{(i)})\) 来尽可能地增大 \(L(\theta)\)。新的参数 \(\theta^{(i+1)}\) 由下式给出：

在对 \(B(\theta, \theta^{(i)})\) 进行最大化时，可以忽略掉与 \(\theta\) 无关的常数项。这等价于最大化一个我们称之为 Q 函数 的部分。

Q 函数 (page 9) ¶

因此，EM 算法的 M 步可以简化为：

这个形式通常比直接最大化 \(L(\theta)\) 简单得多，因为 Q 函数中对数内部不再有求和项。

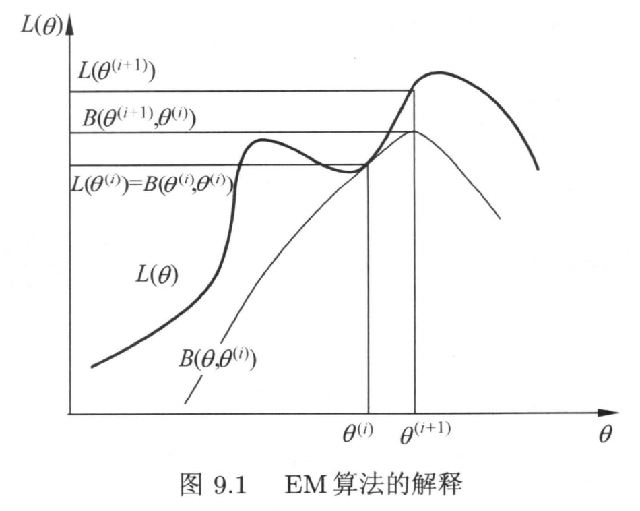
直观解释 (page 10) ¶

EM 算法的迭代过程可以直观地理解为：

1. 在当前的参数 \(\theta^{(i)}\) 处，我们构造了一个 \(L(\theta)\) 的下界函数 \(B(\theta, \theta^{(i)})\)（或 Q 函数）。这个下界函数在点 \(\theta = \theta^{(i)}\) 处与 \(L(\theta)\) 相切，即 \(L(\theta^{(i)}) = B(\theta^{(i)}, \theta^{(i)})\)。
2. 我们寻找一个新的参数 \(\theta^{(i+1)}\) 来最大化这个下界函数。
3. 由于 \(L(\theta) \ge B(\theta, \theta^{(i)})\)，并且我们选择了 \(\theta^{(i+1)}\) 使得 \(B(\theta^{(i+1)}, \theta^{(i)}) \ge B(\theta^{(i)}, \theta^{(i)})\)，因此可以保证 \(L(\theta^{(i+1)}) \ge L(\theta^{(i)})\)。

这个过程确保了每次迭代都会使观测数据的对数似然值单调不减。

从上图可以看出，EM 算法保证了似然函数值的单调增加，但不能保证找到全局最优解。算法的最终结果依赖于初始值的选择，可能会收敛到局部最优值。

EM 算法流程 (page 11-12) ¶

现在，我们可以总结出 EM 算法的完整流程。

EM 算法的收敛性 (page 13-17) ¶

EM 算法具有良好的收敛性质，但理解其收敛的含义至关重要。

EM 算法在高斯混合模型学习中的应用 (page 18-26) ¶

高斯混合模型（Gaussian Mixture Model, GMM）是 EM 算法的一个经典应用场景。

直接对 GMM 的似然函数求极大值非常困难，因为对数里面有求和项。这正是 EM 算法的用武之地。

EM 算法 - 例子 (page 27-30) ¶

这个例子生动地展示了 EM 算法的核心思想：通过“软分配”（计算响应度）来处理不确定性，然后基于这种软分配的结果来更新参数，循环往复，直至收敛。

习题 ¶

• (1) 初始值 : \(\theta^{(0)}=(\pi^{(0)},p^{(0)},q^{(0)})\)；
• (2) E 步 : 第二次抛出 B 硬币概率：

• (3) M 步 : 计算模型参数的新估计值

• (4) 停止条件 : 需要设定迭代停止的条件。常用的条件是：
  • 参数变化足够小 : \(|| θ^{(i+1)} - θ^{(i)} || < ε_{1}\)
  • Q 函数（或对数似然函数 L(θ)）增量足够小 : \(|| L(θ^{(i+1)}) - L(θ^{(i)}) || < ε_{2}\) ( 或使用 Q 函数的变化 ) 其中 ε1, ε2 是预设的很小的正数。

使用 python 进行迭代有：

import numpy as np
import matplotlib.pyplot as plt

observations = np.array([1, 1, 0, 1, 0, 0, 1, 0, 1, 1])
n = len(observations)

# Initial parameters
pi_0 = 0.46
p_0 = 0.55
q_0 = 0.67


# EM algorithm implementation
def em_algorithm(observations, pi_0, p_0, q_0, max_iterations=100, tol=1e-6):
    pi = pi_0
    p = p_0
    q = q_0
    n = len(observations)
    history = []

    for iteration in range(max_iterations):
        history.append((pi, p, q))

        # E-step: Calculate posterior probability that each observation comes from coin A
        mu = np.zeros(n)
        for j in range(n):
            y_j = observations[j]
            numerator = pi * (p**y_j) * ((1 - p) ** (1 - y_j))
            denominator = pi * (p**y_j) * ((1 - p) ** (1 - y_j)) + (1 - pi) * (
                q**y_j
            ) * ((1 - q) ** (1 - y_j))
            mu[j] = numerator / denominator

        # M-step: Update parameter estimates
        pi_new = np.mean(mu)
        p_new = np.sum(mu * observations) / np.sum(mu)
        q_new = np.sum((1 - mu) * observations) / np.sum(1 - mu)

        # Check convergence
        if max(abs(pi_new - pi), abs(p_new - p), abs(q_new - q)) < tol:
            pi, p, q = pi_new, p_new, q_new
            history.append((pi, p, q))
            print(f"EM algorithm converged after {iteration+1} iterations")
            break

        pi, p, q = pi_new, p_new, q_new

    if iteration == max_iterations - 1:
        print(f"EM algorithm reached maximum iterations {max_iterations}")

    return pi, p, q, history


pi_final, p_final, q_final, history = em_algorithm(observations, pi_0, p_0, q_0)
print(f"Initial parameters: π = {pi_0}, p = {p_0}, q = {q_0}")
print(f"Final estimates: π = {pi_final:.6f}, p = {p_final:.6f}, q = {q_final:.6f}")

EM algorithm converged after 2 iterations
Initial parameters: π = 0.46, p = 0.55, q = 0.67
Final estimates: π = 0.461863, p = 0.534595, q = 0.656135

可以看到当前的情况收敛很快，最终 \(\theta = (0.461863, 0.534595, 0.656135)\) 。

由定义 9.3： \(F(\tilde P,\theta)=E_{\tilde P}[\log P(Y,Z|\theta)]+H(\tilde P)\)，其中 \(H(\tilde{P}) = - E_{\tilde P} \log \tilde P(Z)\)；由引理 9.1 得知： \(\tilde{P}_{\theta}(Z)=P(Z|Y, \theta)\) ；故而：

如果这对你有用的话，请给我点个star吧 ===>