跳转至

CNN&RNN

CNN

https://www.huaxiaozhuan.com/%E6%B7%B1%E5%BA%A6%E5%AD%A6%E4%B9%A0/chapters/5_CNN.html

卷积与卷积核

在我们学过的微积分知识中，卷积计算被定义为：

\[ s(t)=(x*w)(t) = \int x(a)w(t-a)da \]

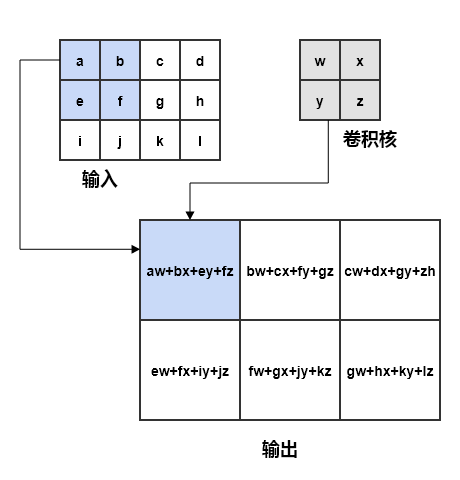
在计算机科学中，计算往往是有限且离散的；在卷积神经网络 (Convolutional Neural Network, CNN) 中，\(x(\cdot)\) 被称为输入，\(w(\cdot)\) 被称为卷积核，输出被称为特征图 (feature map)。卷积运算可以是高纬度的，但一般用于处理二维数据；如果二维图像 I 作为输入，则需要使用二维核函数 K，卷积运算的输出为（这实际上是互相关函数 (cross-correlation)）：

\[ \mathbf{S}(i,j)=(\mathbf{I}*\mathbf{K})(i,j)=\sum_m\sum_n\mathbf{I}(m,n)\mathbf{K}(i-m,j-n) \]
直观理解

在卷积原理及可视化中给出了动图直观的理解“卷积”操作；简单来说，核（往往远小于输入的规模）在输入上进行滑动（每次滑动的距离称为步长 (stride)）；对于核与此时覆盖到的输入逐单元相乘并相加得到一个输出单元；输出单元按顺序构成输出。

https://raw.githubusercontent.com/darstib/public_imgs/utool/2510/07_251007-222932.png

另一方面，卷积也可以看作是除去接收域外其他参数均为 0 的稀疏全连接。

注意到卷积过程中的计算都是相乘且相加，考虑可并行性转变为矩阵相乘；对于长度分别为 M, N 的 \(x(\cdot), w(\cdot)\)，最后输出 \(S\) 的长度应该为 \(L\in[M-N+1, M+N-1]\) （取决于填充情况，常见有三种填充方式 1）；为此先将 x, w 进行填充：

\[ \left.x_p(i)=\left\{\begin{array}{ll}x(i)&,0\leq i\leq M-1\\0&,M-1<i\leq L-1\end{array}\right.\right. ，w_p(i)=\left\{\begin{array}{ll}w(i)&,0\leq i\leq N-1\\0&,N-1<i\leq L-1\end{array}\right. \]

构造 w 的循环矩阵：

\[ \mathbf{W}=\begin{bmatrix}w_p(0)&w_p(L-1)&w_p(L-2)&\cdots&w_p(1)\\w_p(1)&w_p(0)&w_p(L-1)&\cdots&w_p(2)\\\vdots&\vdots&\vdots&\ddots&\vdots\\w_p(L-1)&w_p(L-2)&w_p(L-3)&\cdots&w_p(0)\end{bmatrix} \]

故而可以计算 \(S = W\cdot x_{p}\) 。在神经网络中，卷积运算的作用就类似于滤波，因此也称卷积核为 (filter) 滤波器。

每个卷积核能够提取一个类型的特征，并行使用多个卷积核可以使得输出的特征图具有多个通道 (channel) 。

卷积层

一个卷积层一般包括三个部分：卷积运算部分，非线性激活部分，池化部分。在卷积运算部分包含了三个重要思想：

  1. 稀疏交互：相比于传统网络的全连接层，输出的每一个单元只受少部分集中的输入单元影响，减小了计算和存储开销；随着卷积层的叠加，输出的每一个单元同样能够间接的受到所有输入单元的影响；网络深层的单元格的接收域大于浅层。
  2. 参数共享：相比于传统网络全连接层所有参数独立，在一次卷积运算中共享一个核，也即参数数量 \(M\times M \rightarrow N \times N, M \gg N\)。
  3. 等变表示：（如果 \(f(g(x))= g(f(x))\)，则称 f 对于 g 变换具有等变性）对于输入内容进行某些操作后（如对图像进行平移）并不会影响输出太多。

降 / 下采样 (DownSampling)

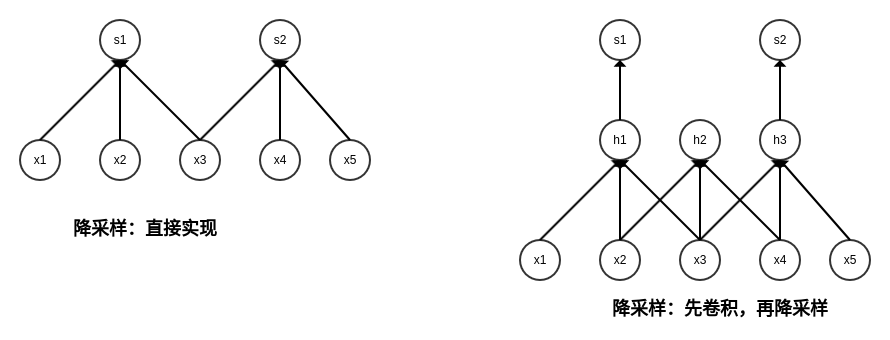
有时候为了降低计算开销，我们适当抛弃一些原本需要计算的点。一般而言我们直接通过调整步长 (stride) 来实现（下图左）；从达到目的的角度来看可以先实现原有的卷积再丢弃，但是显然这样不符合我们降低计算开销的一个目的，故而一般都使用前者。

https://raw.githubusercontent.com/darstib/public_imgs/utool/2510/07_251007-223351.png

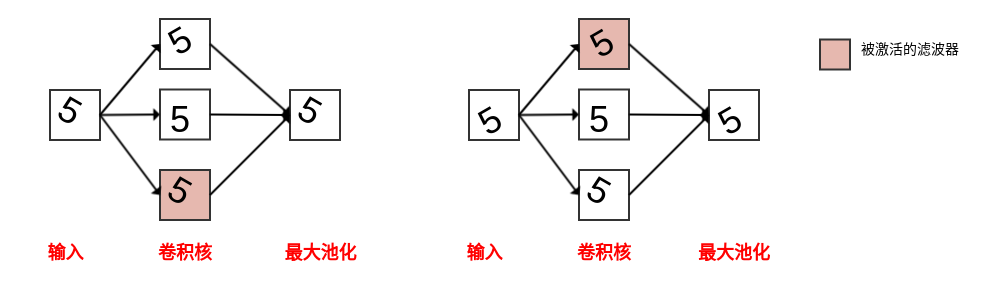
池化 (pooling) 是另一个降采样的方法，它可以看作一个特殊的卷积方式。与卷积相同，池化操作时使用一个滑动窗口进行采样，并进行一种“顺序无关”的操作，如取最大、求平均。池化具有两个特性：

  1. 平移近似不变性：平移变换大体不影响池化操作的结果
  2. 模拟其他不变性：对于旋转等操作可以利用多个核并选择激活以应对
    https://raw.githubusercontent.com/darstib/public_imgs/utool/2510/07_251007-230606.png

RNN

https://www.huaxiaozhuan.com/%E6%B7%B1%E5%BA%A6%E5%AD%A6%E4%B9%A0/chapters/6_RNN.html

循环神经网络 (recurrent neural network, RNN) 是一种用于处理序列数据 \(\mathbf{x}_i=\{\vec{\mathbf{x}}_i^{(1)},\vec{\mathbf{x}}_i^{(2)},\cdots,\vec{\mathbf{x}}_i^{(\tau_i)}\}\) 的神经网络。

传统的前馈神经网络在每个时间点上分配一个独立的参数，因此网络需要学习每个时间点上的权重。而如果前一个时间步和后一个时间步之间的关系与时刻 t 无关，相同参数可以应用于不同的时间步，则循环神经网络在每个时间点上共享相同的权重。

就像几乎所有函数都可以被认为是前馈神经网络，几乎任何涉及循环的函数都可以被认为是循环神经网络。

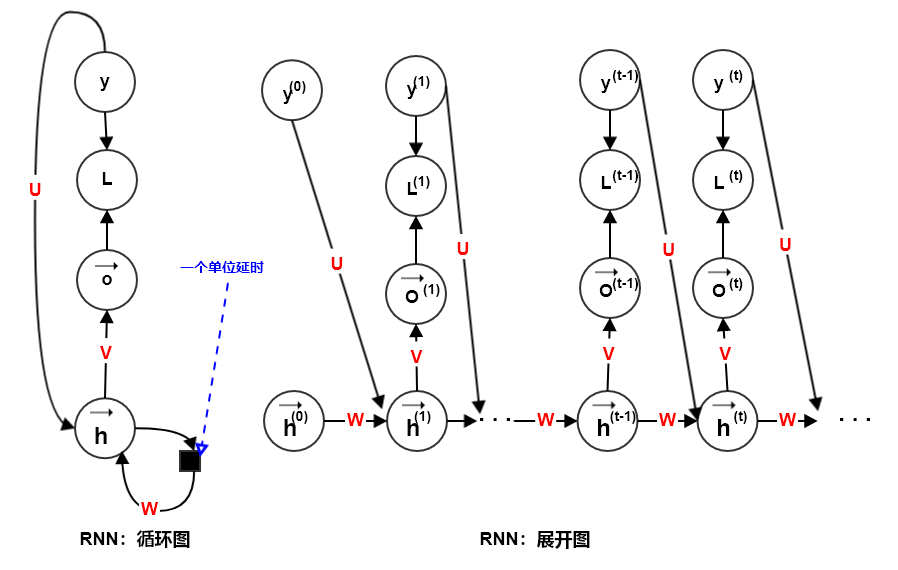
计算图

考虑一个会受到外部影响的动力系统的转移方程：

\[ \vec{\mathbf{h}}^{(t)}=f(\vec{\mathbf{h}}^{(t-1)},\vec{\mathbf{x}}^{(t)};\Theta) \]

其中

  • \(\vec{h}^{(t)}\)：系统状态
  • \(\vec{x}^{(t)}\)：外部影响
  • \(\Theta\)：模型参数
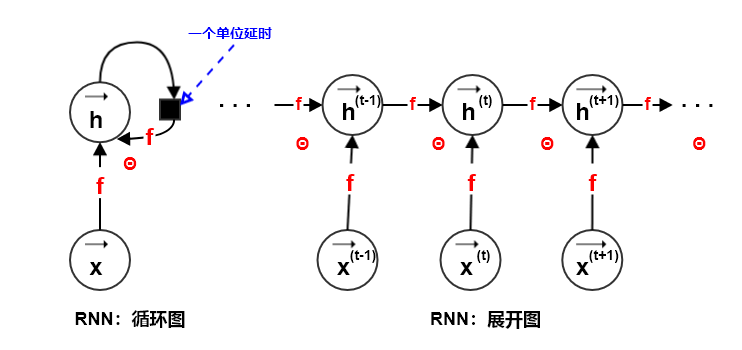
https://raw.githubusercontent.com/darstib/public_imgs/utool/2510/08_1759887460011.png

可以认为，\(\vec{h}^{(t)}\) 是信息序列 \(\mathbf{x}=\{\vec{x}^{(1)}, \vec{x}^{(2)}, \dots, \vec{x}^{(t-1)}\}\) 的一个有损表示（使用了定长的 h 表征变长的 x）；有时会有选择的保留信息序列，例如 attention 机制。

从上述转移方程和展开图我们不难发现：

  • 无论输入序列的长度 \(\tau\) 如何，学得的模型始终具有相同的输入大小。
    • 因为模型在每个时间步上，其模型的输入 \(\vec{x}^{(t)}\) 都是相同大小的。
  • 在每个时间步转移函数 f 是相同的，参数共享。

这提高了模型的泛化性，降低了模型训练成本。

零长度输入

当信息序列的长度为 0 时，则使用历史输出来作为当前时刻的输入（如简单的文本生成任务），得到时间步 \(t\) 输出的 k 分量：

\[o_k^{(t)}=p(y^{(t)}=k\mid y^{(0)},y^{(1)},\cdots,y^{(t-1)}),\quad k=1,2,\cdots,K\]

其中 \(\mathbf{y}^{(t)}=\{y^{(0)}, \dots, y^{(t)}\}\) 为真实标签。损失函数为：

\[ L=-\sum_{t=1}^\tau\sum_{k=1}^K\mathbb{I}(k=y^{(t)})\log o_k^{(t)} \]
https://raw.githubusercontent.com/darstib/public_imgs/utool/2510/08_251008-102601.png

考虑到输入需要定长，使用 \(h^{(t-1)}\) 来有损表征 \(\mathbf{y}^{(t-1)}\) ，同时上一时刻的标签 \(y^{(t-1)}\) 较为重要，故而实际模型为：

\[ \begin{align} \vec{\mathbf{a}}^{(t)}&=\vec{\mathbf{b}}+\mathbf{W}\vec{\mathbf{h}}^{(t-1)}+\mathbf{U}\vec{\mathbf{y}}^{(t-1)}\\ \vec{\mathbf{h}}^{(t)}&=\tanh(\vec{\mathbf{a}}^{(t)})\\ \vec{\mathbf{o}}^{(t)}&=\text{softmax}\left(\vec{\mathbf{c}}+\mathbf{V}\vec{\mathbf{h}}^{(t)}\right) \end{align} \]

单长度输入

模型包含单个 x 作为输入。此时有三种输入方式：输入作为每个时间步的输入、输入作为初始状态、以及这两种方式的结合。

多长度输入

较复杂，这里不讨论。

GRNN

目前实际应用中最有效的序列模型是门控循环神经网络 (Gated Recurrent Neural Network, GRNN)，包括基于长短期记忆 (Long Short-Term Memory, LSTM, 1997) 的 RNN 和基于门控循环单元 (Gated Recurrent Unit, GRU, 2014) 的 RNN 。

LSTM

长短期记忆网络的设计灵感来自于计算机的逻辑门。长短期记忆网络引入了记忆元 (memory cell / cell)。为了控制记忆元，我们需要许多门。

  • 其中一个门用来从单元中输出条目，我们将其称为输出门（output gate, O）。
  • 另外一个门用来决定何时将数据读入单元，我们将其称为输入门（input gate, I）。
  • 我们还需要一种机制来重置单元的内容，由遗忘门（forget gate, F）来管理，

一个记忆元如下所示：

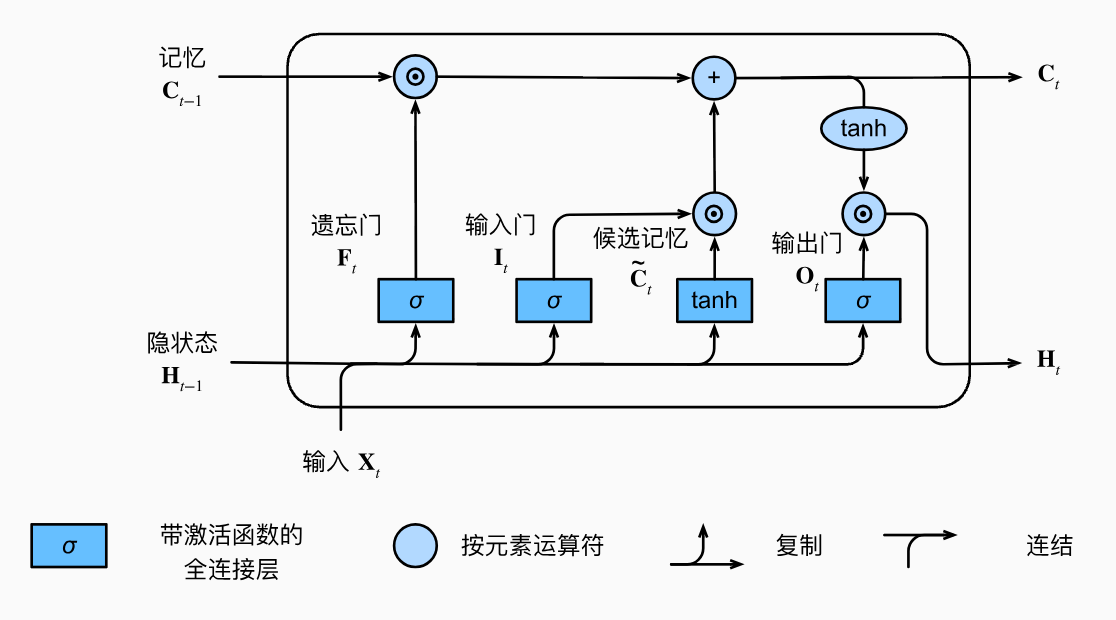
https://raw.githubusercontent.com/darstib/public_imgs/utool/2510/08_251008-215004.png
https://zh.d2l.ai/chapter_recurrent-modern/lstm.html#id6
  • 遗忘门：\(\mathbf{F}_{t}=\sigma(\mathbf{X}_t\mathbf{W}_{xf}+\mathbf{H}_{t-1}\mathbf{W}_{hf}+\mathbf{b}_f) \in [0, 1]\)
  • 输入门：\(\mathbf{I}_{t}=\sigma(\mathbf{X}_t\mathbf{W}_{xi}+\mathbf{H}_{t-1}\mathbf{W}_{hi}+\mathbf{b}_i) \in [0, 1]\)
  • 候选记忆：\(\tilde{\mathbf{C}}_t=\tanh(\mathbf{X}_t\mathbf{W}_{xc}+\mathbf{H}_{t-1}\mathbf{W}_{hc}+\mathbf{b}_c)\)
  • 输出门：\(\mathbf{O}_{t}=\sigma(\mathbf{X}_{t}\mathbf{W}_{xo}+\mathbf{H}_{t-1}\mathbf{W}_{ho}+\mathbf{b}_{o}) \in [0, 1]\)

\(F_{t} \& I_{t}\) 用于控制来自上一记忆元的记忆和当前候选记忆（来自上一记忆元隐状态和当前输入）的比例，进行逐元素相乘后相加作为当前记忆元的记忆输出 \(\mathbf{C}_t=\mathbf{F}_t\odot\mathbf{C}_{t-1}+\mathbf{I}_t\odot\tilde{\mathbf{C}}_t\) ；输出门则与 tanh 激活后的 \(C_{t}\) 进行逐元素相乘作为当前记忆元的隐状态输出。

获得隐状态后与 RNN 操作一致。

GRU

GRU 的设计更加简单：

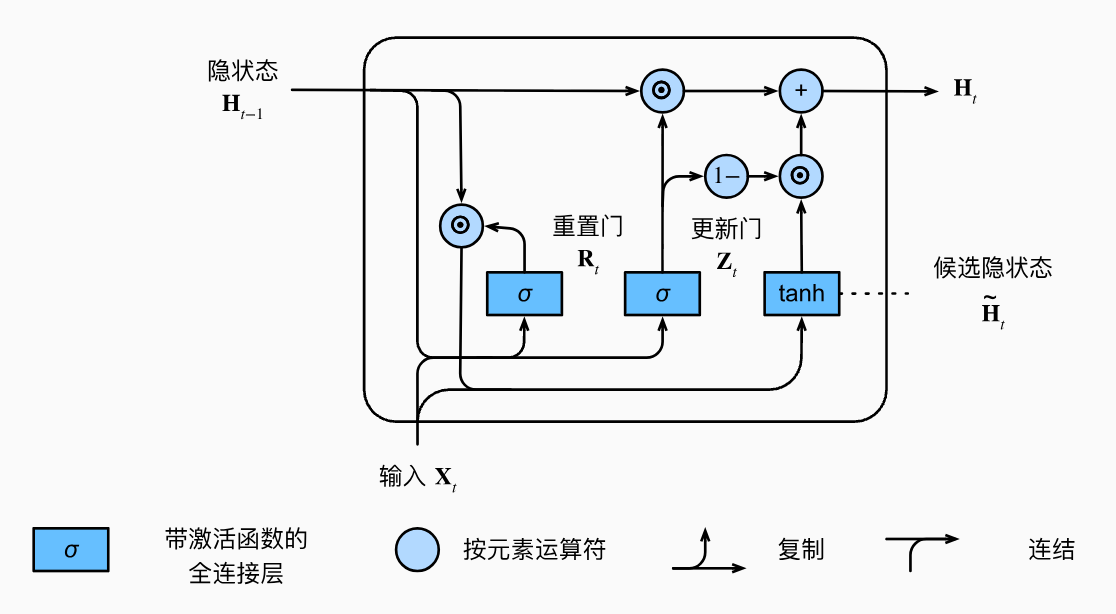
https://raw.githubusercontent.com/darstib/public_imgs/utool/2510/08_251008-221227.png
https://zh.d2l.ai/chapter_recurrent-modern/gru.html#id7
  • 重置门：\(\mathbf{R}_{t}=\sigma(\mathbf{X}_t\mathbf{W}_{xr}+\mathbf{H}_{t-1}\mathbf{W}_{hr}+\mathbf{b}_r)\)
  • 更新门：\(\mathbf{Z}_{t}=\sigma(\mathbf{X}_t\mathbf{W}_{xz}+\mathbf{H}_{t-1}\mathbf{W}_{hz}+\mathbf{b}_z)\)
  • 候选隐藏态：\(\tilde{\mathbf{H}}_t=\tanh(\mathbf{X}_t\mathbf{W}_{xh}+(\mathbf{R}_t\odot\mathbf{H}_{t-1})\mathbf{W}_{hh}+\mathbf{b}_h)\)
  • 隐藏态：\(\mathbf{H}_t=\mathbf{Z}_t\odot\mathbf{H}_{t-1}+(1-\mathbf{Z}_t)\odot\tilde{\mathbf{H}}_t\)

其余部分与 RNN 一致。

  1. 三种填充方式：

    1. valid 填充，也即不填充，只计算在输入能够完全包裹核的结果；对于宽度为 K 的核，每次计算后的输出的规模减小 K-1；也即此时 \(L = M-(N-1)\)；
    2. same 填充，即确保输出与输入同规模的填充 0；优点在于这样可以任意堆叠层数，缺点在于边缘单元被不断弱化；
    3. full 填充，也即只要输入和核有重叠部分即可计算，其余部分全部填充 0；每个输入单元都恰好被访问了 K 次，每次计算后输出的规模增大 K-1，也即此时 \(L = M + (N-1)\)。

    ↩

评论