跳转至

Graph Embedding

在 Word2vec 和 Item2vec 中我们的嵌入都是从序列信息中去学习的，这种思路面对错综复杂的图结构时似乎有些力不从心了。

考虑目标：基于一个图 \(G = (V, E), E\subseteq(V\times V)\) 学习一个映射 \(\Phi: V \rightarrow \mathbb{R}^{d}\) 以将图上的节点嵌入。

Perozzi 等人受到 word2vec 的启发，考虑在图中先进行随机游走生成节点序列，然后应用 Skip-gram 算法——利用节点的共现——学习嵌入表示，这就是 DeepWalk，其他 Graph embedding 算法也是类似的。

社交网络表示

早期的 Graph Embedding 在社交网络上进行，所以学习的一般是节点之间的关系情况，但是描述为“相似度”也是大差不差的。完整而言，带标签的社交网络表示为 \(G_{L} = (V, E, X, Y)\)，其中：

  • \(X \in \mathbb{R}^{|V|\times |S|}\) 表示特征，S 是每个节点的特征空间
  • \(Y \in \mathbb{R}^{|V| \in |\mathcal{Y}|}\) 表示标签，\(\mathcal{Y}\) 为节点的标签空间

更早的机器学习只是学习 \(X \rightarrow Y\) 的映射，忽略节点与节点之间的关系。

频次幂律分布

如果一个图中顶点的度degree 满足幂律分布 power law，则随机游走序列中顶点出现的频次也满足幂律分布。

自然语言中单词的出现频率符合幂律分布，而 short random walk（长度有限）结果发现节点出现的频率也符合幂律分布！

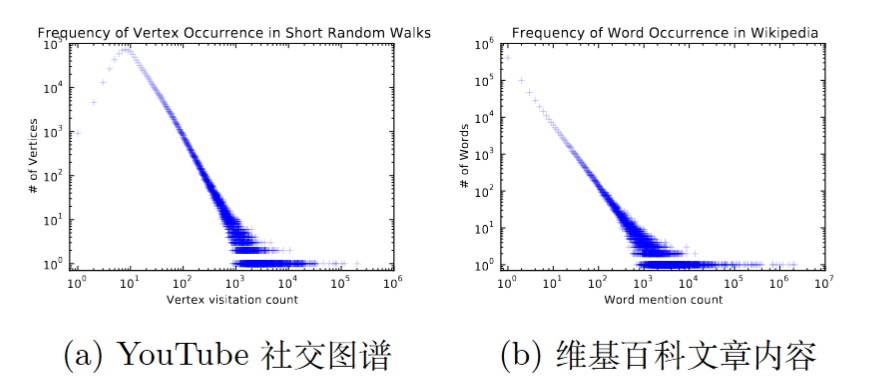
https://raw.githubusercontent.com/darstib/public_imgs/utool/2509/05_250905-134154.png

youtube graph & wikipedia articles

因而借助随机游走将 word2vec 迁移至图学习中理论具有可行性：

  • 序列 == 语句
  • 图所有节点 == 库所有单词

DeepWalk

DeepWalk 由两部分组成：

  1. 随机游走序列生成
  2. Skip-Gram 参数更新

随机游走序列生成

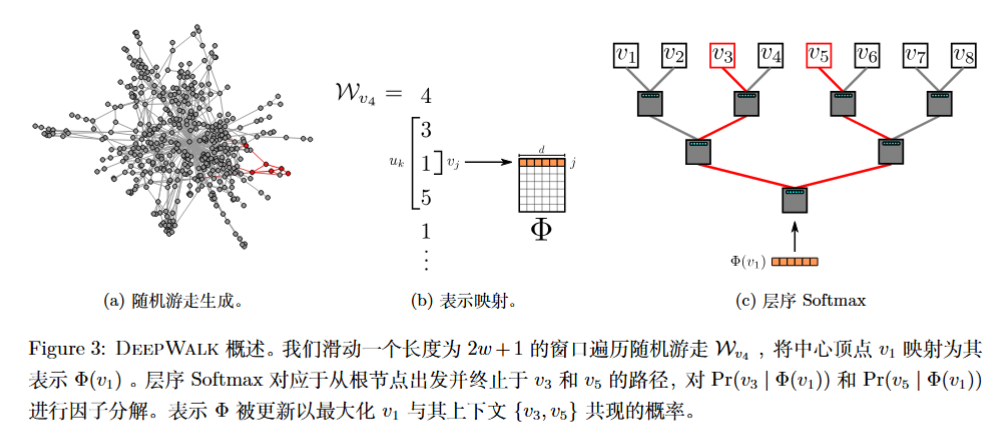
基于特定的游走策略（默认为等概率随机）和限定序列长度（限定的长度可以动态调整，就像语句长度参差不一）生成随机游走序列 \(\mathcal{W}\) 。

随机游走序列

定义以 \(v_{i}\) 开始的一次随机游走序列为 \(\tilde{\mathcal{W}}_{v_{i}}=(\mathcal{W}_{v_{i}}^{1},\cdots,\mathcal{W}_{v_{i}}^{k},\cdots,\mathcal{W}_{v_{i}}^{t})\)，t 为序列长度，依次随机寻找（改进版中也有按权重重新分配概率）邻居。

Skip-Gram

在 Skip-gram(SG) 处介绍了 SG 算法在 word2vec 的应用，不难发现我们期望学习的映射 \(V \rightarrow \mathbb{R}^{d}\) 在模型中应该作为一个矩阵：\(\Phi \in \mathbb{R}^{|V| \times d}\) ，\(\Phi\) 的每一个行向量即为对应节点的嵌入表达，在开始被随机初始化。同样的，我们将遇到因为节点数量过多导致的不可接受的 Softmax 计算量问题；论文中考虑层序 Softmax (Hierarchical Softmax, see section Skip-gram(SG) ) 。

DeepWalk

https://raw.githubusercontent.com/darstib/public_imgs/utool/2509/05_250905-143542.png
Overview of DeepWalk
Algorithm 1: DeepWalk(G, w, d, γ, t)
Input:
  - Graph G = (V, E)
  - Window size w
  - Embedding dimension d
  - Walks per vertex γ
  - Walk length t

Output:
  - Φ ∈ R^{|V|×d}  // matrix of vertex representations

Procedure:
  1. Φ ← SampleUniform(|V|, d)          // initialize embeddings
  2. T ← BuildBinaryTree(V)             // e.g., for hierarchical softmax
  3. for i ← 0 to γ do
  4.     O ← Shuffle(V)
  5.     for each v ∈ O do
  6.         W_v ← RandomWalk(G, v, t)
  7.         SkipGram(Φ, W_v, w)        // update Φ using Skip-Gram on walk W_v
  8.     end for
  9. end for
 10. return Φ

Large-scale Information Network Embedding (LINE)

我们期望在理想的低维空间 \(\mathbb{R}^{d}\) 中能够保留顶点间的一阶邻近度和二阶邻近度（下面将解释）；同时为了面对真实业务，在大规模带权网络上应该仍然可行。

  • 更为传统的 GE 方法（如 LLE, Laplacian eigenmap）只能够捕捉一阶邻近度，且无法处理大规模网络；
  • DeepWalk （经典版）只能够处理无权图，没有明确区分一阶邻近度和二阶邻近度。

《LINE: Large-scale Information Network Embedding》提出 LINE 满足了以上要求。

符号声明

原论文中 \(i, j, u, v, w_{i, j}, w_{u, v}, v_{i / j}, \vec{u}_{i / j}\) 乱起八糟的给我看吐了，一会用 u, v 表示节点 id 一会表示嵌入向量（当然不太影响理解，如果业内都就是这么用的那无话可说……）

无论如下，在下面的内容中

  • i, j 表示节点 id，\(w_{i, j}\) 表示边 (i, j) 的权重
  • u 表示二阶邻近度向量，v 表示一阶邻近度向量
  • \(\vec{u}\) 表示二阶邻近度向量中的两种

邻近度

一阶邻近度

记顶点对 (i, j) 之间的一阶邻近度 (first-order proximity) 为权重 \(w_{i, j}\)，来刻画顶点 u, v 之间的相似 / 邻近关系程度。如果两个顶点之间没有边，则其一阶邻近度为 0。

对于带权图，我们定义嵌入向量为 \(v_{i}, v_{j}\) 顶点对 (i, j) 的：

  • 经验概率分布 \(\hat{p}_{1}(i, j) = \frac{w_{i, j}}{W}\)，其中 \(W = \sum_{(i, j)\in E} w_{i, j}\) 即权重和。
  • 联合概率分布 \(p_{1}(i, j) = \sigma(v_{i}\cdot v_{j})\)，其中 \(\sigma(x) = 1/1+e^{-x}\)

目标损失函数定义为（\(d(\cdot, \cdot)\) 为概率分布距离度量，论文中使用 KL 散度）

\[ O_1=\sum_{(i,j)\in E}d(\hat{p}_1(i,j),p_1(i,j))=\frac{1}{W}\sum_{(i,j)\in E}w_{i,j}\times\log (1+ e^{-v_{i}\cdot v_{j}}) \]

一阶显然这里针对的是无向图，有向图则丢失了方向信息。

二阶邻近度

但是真实世界的信息网络总是难以观测全面，未观测到的边可能将两个关系密切的顶点误判为“没有关系”。基于“社交网络中，共同好友较多的两个人很可能也认识”的思路 1，我们采用二阶邻近度 (second-order proximity) 来衡量可能潜在的关系。

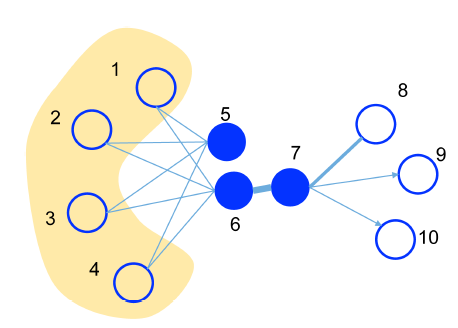
https://raw.githubusercontent.com/darstib/public_imgs/utool/2509/05_1757055302553.png
second-order proximity

定义 \(\mathbf{P_{u}} = (w_{u, 1}, w_{u, 2}, \dots, w_{u, |V|})\) 为顶点 u 与其他所有点的一阶邻近度，参考一阶邻近度的训练和 Skip-gram，二阶邻近度被描述为：\(\mathbf{P}_{u}\) 和 \(\mathbf{P}_{v}\) 的相似度。如果 u, v 之间没有任何邻居，认为其二阶邻近度为 0 。

\(w_{u, u} =\ ?\)

注意到论文中定义 Second-order Proximity 时，\(\mathbf{P_{u}} = (w_{u, 1}, w_{u, 2}, \dots, w_{u, |V|})\) 的长度为 |V|，这意味着包括图中全部节点，其中包括了一个 First-order Proximity: \(w_{u, u}\)。

论文中没有明确说明节点和自身的一阶邻近度是多少，权且认为没有自环边故而默认为 0。

对于有向图，我们定义嵌入向量为 \(\vec{u}_{i}, \vec{u}_{j}'\) 有向边 (i, j) 的：

  • 经验概率为 \(\hat{p}_{2}(j \mid i) = \frac{w_{i, j}}{d_{i}}\)，其中 \(d_{i} = \sum_{k \in N(i)} w_{i, k}\) 表示 i 所有出边的权重和
  • 条件概率为 \(p_2(j\mid i)=\text{softmax}(u_j'\cdot\vec{u}_i)\)，其中 \(\text{softmax} (u_j'\cdot\vec{u}_i) = \frac{\exp(u_j'\cdot\vec{u}_i)}{\sum_{k=1}^{|V|}\exp(\vec{u}_k'\cdot\vec{u}_i)}\)

目标损失函数定义为（\(\lambda _{i}\) 表示 \(v_{i}\) 在网络中的重要性，论文中使用 \(d_{i}\)；softmax 使用基于出度的负采样优化）：

\[ O_2 = \sum_{i\in V}\lambda_i d(\hat{p}_2(j\mid i), p_2(j\mid i)) = -\sum_{(i, j) \in E} w_{i, j} \log \left( \frac{\exp(\vec{u}_j' \cdot \vec{u}_i)}{\sum_{k \in V}\exp(\vec{u}_k' \cdot \vec{u}_i)} \right) \]

二阶邻近度适用于有向图，无向图将无向边视为双向的同权边也可以适用。

Edge Sampling

在优化 \(O_{2}\) 时发现：

\[ \nabla_{\vec{\mathbf{u}}_i}O_2=w_{i,j}\times\nabla_{\vec{\mathbf{u}}_i}\log p_2(j\mid i) \]

即梯度中都乘以了边权重 \(w_{i, j}\)，如果权重区别非常大，在进行梯度下降法优化时学习率将非常难选择

思路一：带有 \(w_{i,j}\) 权重的边拆分为 \(w_{i, j}\times \Delta\) 条边，其中 \(\Delta\) 仅是为了让边数为正整数

思路一能够解决问题，但是存储空间成本提升较多。

思路二：将权重 \(w_{i,j}\) 转而看作概率（对权重归一化）进行采样，等价于思路一。

思路二节约了空间成本，但是平均采样一条边花费 \(O(|E|)\) 时间；采用 Alias Method 可以降至 \(O(1)\) （参见 Alias Method: 时间复杂度 O(1) 的离散采样方法）。

向量融合

LINE 分别训练了一阶邻近度模型和二阶邻近度模型，分别得到一阶向量 \(v_{i}\) 和二阶向量 \(u_{i}\)：

  • 监督学习：将向量拼接 \(e_{i} = [v_{i}, u_{i}]\) 并可以通过逻辑回归模型调整融合权重；
  • 无监督学习：没法确定权重，只能够单独使用

虽然一直在强调基于带权图，对于无权图视为所有边等权即可。

模型优化

  • 当某些顶点邻居非常少时，可能需要结合邻居的邻居的信息
  • 当加入新节点时，只需要优化 \(-\sum_{j\in N(i)}w_{ji}\log p_1(v_j,v_i), -\sum_{j\in N(i)}w_{ji}\log p_1(v_j|v_i)\) 即可

如果新节点与已有节点的关系也非常少甚至没有，可能需要参考 EGES，使用辅助信息来表征。

  1. 其实这也比较符合 "You shall know a word by the company it keeps" 的思想，人在社会中的身份由你和起他人的关系决定。 ↩

评论