跳转至

Graph Neural Network

很多领域的数据关系可以表示为图结构，如计算机视觉、分子化学、模式识别、目标检测等，这些图结构往往比较复杂，基本的 Graph Embedding （可以认为是将图“压缩”为实值向量）会损失较多信息（如损失了节点的拓扑依赖性），难以捕捉到图的细节。

关于图的任务可以分为两大类：

  • 基于图的任务 (graph-focused) ：例如分子化合物整个图结构的意义高于单独的原子和化学键
  • 基于节点的任务 (node-focused) ：例如目标检测、网页分类任务需要关注局部，整体信息过于嘈杂

论文《The graph neural network model》提出了 GNN 模型，该模型扩展了 RNN 和马尔可夫链技术（它们在预处理阶段尽可能地保留数据的图结构特性），适合处理图结构的数据。GNN 是基于消息扩散机制 (information diffusion mechanism)。图由一组处理单元来处理，每个处理单元对应于图的一个顶点。GNN 既适合 graph-focused 任务，也适合 node-focused 任务。

感觉要先看 CNN&RNN。

值得一提的是，《Computation capabilities of graph neural networks》已经证明了 GNN 展示出一种普遍的逼近特性，并且在不严厉的条件下，GNN 可以逼近图上大多数实际有用的函数。

GNN

模型建立

GNN 所考虑的领域是图 - 节点对（graph, node pair）的集合，记为 \(\mathcal{D} = \mathcal{G} \times \mathcal{N}\)，其中 \(\mathcal{G} = {\mathbf{G}_1, \mathbf{G}_2, \cdots}\) 表示图的集合，\(\mathcal{N} = {\mathbf{N}_1, \mathbf{N}_2, \cdots}\) 表示这些图对应的节点集合的集合。具体而言，数据集 \(\mathcal{L}\) 可以表示为一系列三元组的集合：

\[\mathcal{L} = \{(\mathbf{G}_i, n_{i,j}, \mathbf{t}_{i,j}) \mid \mathbf{G}_i = (\mathbf{N}_i, \mathbf{E}_i) \in \mathcal{G}, n_{i,j} \in \mathbf{N}_i, \mathbf{t}_{i,j} \in \mathbb{R}^m, 1 \leq i \leq p, 1 \leq j \leq q_i\}\]

在这个表示中，\(\mathbf{G}_i\) 表示第 \(i\) 个图，由节点集 \(\mathbf{N}_i\) 和边集 \(\mathbf{E}_i\) 构成；\(n_{i,j}\) 表示图 \(\mathbf{G}_i\) 中的第 \(j\) 个节点；\(\mathbf{t}_{i,j}\) 表示节点 \(n_{i,j}\) 的期望目标（desired target），该目标可能是向量形式，也可能是标量形式。这里约束条件为 \(p \leq |\mathcal{G}|\) 和 \(q_i \leq |\mathbf{N}_i|\)，表明我们考虑的图数量和每个图中的标注节点数量都是有限的。

更为重要的是，\(\mathcal{D}\) 中所有的图都可以组合成一个唯一的、断开的大图，因此可以将 \(\mathcal{D}\) 视为一个配对 \(\mathcal{L} = (\mathbf{G}, \mathcal{T})\)。在这个统一表示中 :

  • \(\mathbf{G} = (\mathbf{N}, \mathbf{E})\) 是包含所有节点和所有边的大图，它是所有子图的并集；
  • \(\mathcal{T} = {(n_i, \mathbf{t}_i) \mid n_i \in \mathbf{N}, \mathbf{t}_i \in \mathbb{R}^m, 1 \leq i \leq q}\) 则表示所有标注节点及其对应目标值的集合。

值得强调的是，这种紧凑的定义方式不仅因为其简洁易用，而且它还直接捕捉到了一些问题的本质特征。在许多实际应用场景中，领域（domain）实际上仅由一个图组成，例如大部分的网络结构，如下图所示的万维网（web network）就是一个典型例证。在这种情况下，看似独立的多个子图实际上通过各种连接关系构成了一个统一的大图结构，因此采用统一大图表示不仅在数学上更为简洁，而且在语义上也更准确地反映了问题的真实结构。

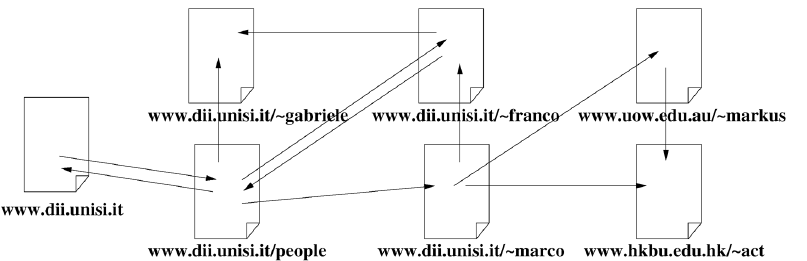
https://raw.githubusercontent.com/darstib/public_imgs/utool/2510/08_251008-152821.png

模型思想

图中的每个节点代表一个概念，而概念应当由自身的特征和相关的概念共同定义。考虑用 \(\mathbf{\vec{h}}_{n}\) 表示节点 n 的概念（有时也称隐藏状态，一般使用最初节点的自身特征进行初始化），定义一个局部转移函数 \(f_{w}(\cdot)\) 满足：

\[ \vec{\mathbf{h}}_n=f\left(\vec{l}_n,\vec{l}_{\mathrm{co}[n]},\vec{\mathbf{h}}_{\mathrm{ne}[n]},\vec{l}_{\mathrm{ne}[n]}\right) \]

并定义一个局部输出函数 \(g(\cdot)\) 获得输出（即这个概念 \(\mathbf{\vec{h}}_{n}\) 能说明什么）：

\[ \vec{\mathbf{o}}_n=g_{w}\left(\vec{\mathbf{h}}_n,\vec{l}_n\right) \]

需要注意的是，\(\vec{h}_{n}\) 是循环定义，即邻居的概念也依赖于节点 n；且领域的扩张是指数级的；f/g 函数是具有可学习参数的。如果对节点进行了简单分类，那么同类的节点共享参数，不同类节点参数互不影响；出于简单，我们认为下面讨论的图中节点都是同一类。

将所有向量进行对应的拼接，有：

\[ \begin{aligned}\vec{\mathbf{h}}&=F_{{\mathbf{w}}}\left(\vec{\mathbf{h}},\vec{l}\right)\\ \vec{\mathbf{o}}&=G_{{\mathbf{w}}}\left(\vec{\mathbf{h}},\vec{l}_{{\mathbf{N}}}\right)\end{aligned} \]

此时 \(F_{\mathbf{w}}, G_{\mathbf{w}}\) 称为全局转移 / 输出函数。它们共同定义了一个映射：\(\varphi_{\mathbf{w}}:\mathcal{D}\to\mathcal{R}^{m}\)，输入一个大图，输出各个顶点的输出。

方程求解

根据巴拿赫不动点定理 (Banach's fih point theorem)，\(\vec{\mathbf{h}}=F_{{\mathbf{w}}}\left(\vec{\mathbf{h}},\vec{l}\right)\) 有唯一解当 \(F_{\mathbf{w}}(\cdot)\) 是一个收缩映射 (contraction map)，即：

\[ \begin{aligned} &\left\|F_{{\mathbf{w}}}\left(\vec{\mathbf{h}},\vec{l}\right)-F_{{\mathbf{w}}}\left(\vec{\mathbf{y}},\vec{l}\right)\right\|\leq\mu\left\|\vec{\mathbf{h}}-\vec{\mathbf{y}}\right\| \\ &\quad\quad\quad\quad s.t. \forall\ 0 \leq \mu \leq 1, \vec{h}, \vec{y} \end{aligned} \]

成立（）。在 GNN 中，这个条件通过适当选择转移函数来满足（例如，可以通过为 \(F_{\mathbf{w}}\) 对 \(\mathbf{\vec{h}}\) 的偏导添加约束）。

考虑迭代式：\(\vec{\mathbf{h}}(t+1)=F_\mathbf{w}\left(\vec{\mathbf{h}}(t),\vec{l}\right)\)，对于任意初始值，\(\mathbf{\vec{h}_{t}}, t \rightarrow \infty\) 都将收敛到 \(\vec{\mathbf{h}}=F_ {{\mathbf{w}} }\left(\vec{\mathbf{h}},\vec{l}\right)\) 的解；同时 \(\mathbf{\vec{o}}_n(t)=g_\mathbf{w}\left(\mathbf{\vec{h}}_n(t),\vec{l}_n\right),\quad n\in\mathbf{N}\) 来计算输出。

这两个函数可以视为一个处理单元，多个处理单元共同组成一个神经网络，被称为编码网络 (encoding network) 。当 \(f(\cdot), g(\cdot)\) 使用前馈神经网络实现时，整个编码网络变为 RNN，如下依次为“图”，“编码网络”，“展开图”。

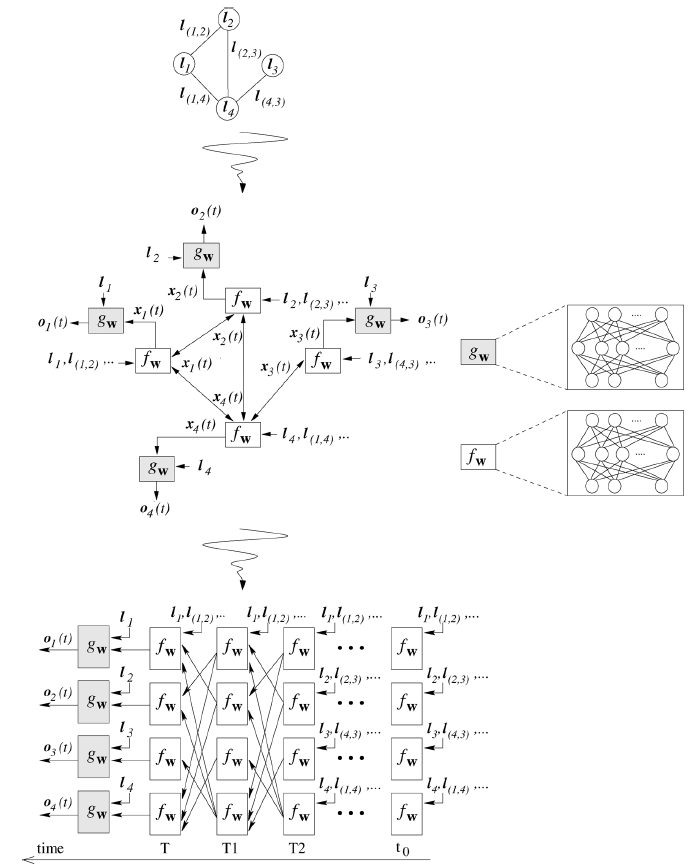
https://raw.githubusercontent.com/darstib/public_imgs/utool/2510/08_251008-171547.png
GNN vs. RNN

看到这里不难发现 GNN 与 RNN 有其相似之处，主要在于其参数共享、迭代执行……（初代 GNN 也被称为 Recurrent-based GNN）；不同之处主要在于：

  • GNN 基于不动点理论，其展开程度由是否收敛和收敛程度决定的；RNN 的展开程度则取决于序列长度。
  • GNN 每次都输入了所有节点，信息流动由边决定；RNN 每次输入对应时间步的节点，信息流动由序列顺序决定。

参数学习

考虑映射 \(\varphi_{w}\) 和数据集 1

\[ \mathcal{L} = \{(\mathbf{G}_i, n_{i,j}, \mathbf{t}_{i,j}) \mid \mathbf{G}_i = (\mathbf{N}_i, \mathbf{E}_i) \in \mathcal{G}, n_{i,j} \in \mathbf{N}_i, \mathbf{t}_{i,j} \in \mathbb{R}^m, 1 \leq i \leq p, 1 \leq j \leq q_i\} \]

则其损失函数可以定义为：

\[ e_\mathbf{w}=\sum_{i=1}^p\sum_{j=1}^{q_i}\left(\mathbf{t}_{i,j}-\mathbf{o}_{i, j}\right)=\sum_{i=1}^p\sum_{j=1}^{q_i}\left(\mathbf{t}_{i,j}-\varphi_\mathbf{w}(\mathbf{G}_i,n_{i,j})\right) \]

使用梯度下降算法来求解最优化问题，较复杂这里暂时不展开。

局限性

GNN 的核心观点是 通过结点信息的传播使整张图达到收敛，在其基础上再进行预测 ，这导致了一些问题：

  • GNN 专注于为节点寻找概念 / 隐藏状态，边只是作为信息流动的依据；
  • \(F_{\mathbf{w}}\) 必须是压缩映射，否则可能不收敛；
  • 在某些情况下基于不动点的收敛会导致节点之间的隐藏状态间存在较多信息共享，从而导致节点的状态太过光滑(Over Smooth)，并且属于结点自身的特征信息匮乏(Less Informative)。

GRNN

类似于 GRNN，门控图神经网络 (Gated Graph Neural Network, GGNN) 被提出以应对经典 GNN 的局限性，从简单性来看参考 GRU，将邻居节点的信息作为输入，自身信息视为隐状态，更新如下：

\[ \mathbf{h}_v^{t+1}=\mathrm{GRU}(\mathbf{h}_v^t,\sum_{u\in ne[v]}\mathbf{W}_{edge}\mathbf{h}_u^t) \]

其中引入一个可学习参数 \(\mathbf{W}_{edge}\) 来针对不同类型的边进行区分。

GCNN

为什么研究者们要设计图卷积操作，传统的卷积不能直接用在图上吗？

图像 ( 欧式空间 ) 与 图 ( 非欧空间 ) 的布局非常不同。图像中像素排列整齐，节点的邻居数量 (4/8) 和相对位置是固定的；而在图中则不固定。

图卷积的本质是想找到适用于图的可学习卷积核，主流研究思路有：

  • 找出一种可处理变长邻居结点的卷积核在图上抽取特征；
  • 提出一种方式把非欧空间的图转换成欧式空间。

目前 GCN 主要有两类：

  • 一类是基于空域的，在原始信号空间直接进行的卷积操作，可以类比到直接在图片的像素点上进行卷积
  • 一类是基于频域的，在频率空间进行的操作，可以类比到对图片进行傅里叶变换后，再进行卷积
    • 如 Spectral CNN 和 ChebNet

空域卷积 (Spatial Convolution)

在图像处理中，空域指的就是图像的像素空间本身。一个 CNN 卷积核在图像上滑动，实际上就是在空域中聚合像素邻居的信息。在图论中，空域指的是图的节点和边的结构本身。空域构建的核心目标就是：如何在图这种不规则的结构上，模拟出类似图像的“局部性”和“多分辨率”，从而让 CNN 的思想可以被迁移过来。

为此我们使用 \(\mathbf{G} = (\mathbf{\Omega}, \mathbf{W})\) 来定义一个加权图，其中 \(\Omega\) 代表图的节点集合（大小为 m）， \(W \in \mathbb{R}^{m\times m}\) 为对称（无向图）、非负的权重矩阵。

局部性 (Locality)

在图像中，一个像素的邻居是其周围的 8 个像素；在图上，我们在 W 上定义节点 j 的领域：

\[ \mathcal{N}_\delta(j)=\{i\mid i\in\boldsymbol{\Omega},W_{i,j}>\delta, \delta > 0\} \]

直观上理解，只有连接足够强（权重超过阈值）的两个节点，我们才认为他们是邻居；则被成为 sparse filter 。

多尺度聚类 (Multiscale Clustering)

CNN 通过池化、降采样操作可以不断缩小特征图的尺寸，从而提取出更加宏观的特征。例如下图：

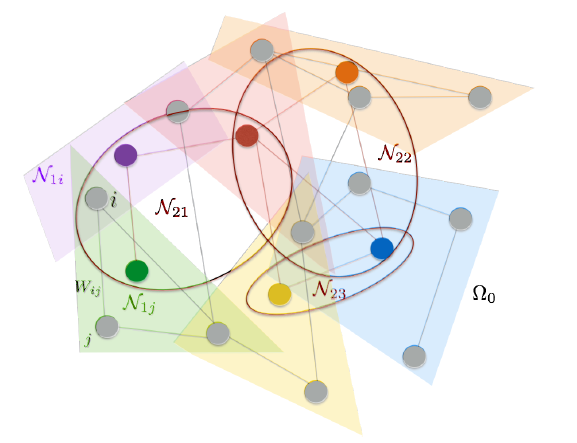
https://raw.githubusercontent.com/darstib/public_imgs/utool/2510/11_251011-183153.png
  1. 原始层 (Level 0)：
    • 代表最底层的 12 个灰色节点，这是我们的原始数据，就像一张高清大图里的像素点。
  2. 第一层聚类 (Level 1)：彩色区域块
    • 系统将原始的 12 个节点 聚类成了 6 个“小团体”。每个小团体用一个彩色区域表示（如黄色、紫色、淡蓝色区域）。
    • 每个小团体内部都有一个中心节点（用彩色标出，如 N₁₁）。
  3. 第二层聚类 (Level 2)：彩色大椭圆
    • 现在，系统将第一层产生的 6 个“小团体”再次进行聚类，形成了 3 个“大联盟”。这 3 个大联盟用红、蓝、橙三个大椭圆（如N₂₁ ,N₂₂ ,N₂₃）表示。

MPNN

在论文《Neural Message Passing for Quantum Chemistry》中给出一个监督学习框架：消息传递神经网络 (Message Passing Neural Network, MPNN) 。它抽象了当时几个最有前景的图神经模型之间的共性，将空域卷积分解为了三个过程：消息传递、状态更新、读出，分别由 \(M_{t}(\cdot), U_{t}(\cdot), R(\cdot)\) 三个待学习函数构成。

  • 消息传递阶段，执行 T 个时间步：
\[ \mathbf{\vec{m}}_v^{(t+1)}=\sum_{u\in\mathcal{N}_v}M_t\left(\mathbf{\vec{h}}_v^{(t)},\mathbf{\vec{h}}_u^{(t)},\mathbf{\vec{e}}_{v,u}\right) \]
  • 状态更新阶段，也需要执行 T 个时间步：
\[\mathbf{\vec{h}}_v^{(t+1)}=U_t\left(\mathbf{\vec{h}}_v^{(t)},\mathbf{\vec{m}}_v^{(t+1)}\right),\quad\mathbf{\vec{h}}_v^{(0)}=\mathbf{\vec{x}}_v \]
  • 读出阶段，根据所有节点在 T 时刻的状态计算整个图的 embedding 向量（参考这篇文章）：
\[ \hat{\vec{\mathbf{y}}}=R\left(\left\{\vec{\mathbf{h}}_v^{(T)}\mid v\in\mathbf{G}\right\}\right) \]

通过设计不同的 \(M_{t}(\cdot), U_{t}(\cdot), R(\cdot)\) ，尽可能逼近每一部分的极限来改进模型。

这看起来与 GGNN 有点像，但不同的是，GGNN 参考了 RNN，是利用级联的时间来捕捉邻居信息；而 MPNN 利用级联的多个层来捕捉邻居信息。可以认为，GGNN 是 MPNN 每层参数都共享的版本。

GraphSAGE

见下文 GraphSAGE 。

频域卷积 (Spectral Convolution)

卷积定理
\[ (f*g)=F^{-1}[F[f]\odot F[g]] \]

其中：

  • f 是原始信息（节点特征）
  • g 是卷积核
  • F 是傅里叶变换，\(F^{-1}\) 是傅里叶逆变换
  • \(\odot\) 是哈达玛乘积，即逐元素乘积

卷积定理为在空 / 时域上的卷积操作变为频域上的哈达玛乘积提供了可能。此时的重点在于如何在图上进行傅里叶（逆）变换。

定义图的拉普拉斯矩阵为度矩阵减去其邻接矩阵，即：\(L = D - A\) 。

https://raw.githubusercontent.com/darstib/public_imgs/utool/2510/11_251011-164109.png

在 AI 算法工程师手册 GNN 中证明了 \(\nabla^2\vec{\mathbf{f}}=\mathbf{L}\vec{\mathbf{f}}\) 即图的拉普拉斯算子即拉普拉斯矩阵。

对于无向图，L 一定是一个对称矩阵，可以被谱分解为：

\[ \begin{aligned} &L=U\Lambda U^T\\ &U=(u_1,u_2,\cdots,u_n) \in \mathbb{R}^{n\times n}\\ &\Lambda=\begin{bmatrix} \lambda_1&\ldots&0\\ \ldots&\ldots&\ldots\\0&\ldots&\lambda_n\end{bmatrix} \end{aligned} \]

其中 U 是由 L 的特征向量构成的正交矩阵，可以看作是图的傅里叶基，每一列 \(u_{i}\) 代表一个“频率”；\(\Lambda\) 是由 L 的特征值构成的对角矩阵，每一个值 \(\lambda _{i}\) 代表了“频率”的大小。

那么图傅里叶变换就是将 f 投影到傅里叶基 U 张成的空间中：\(\hat{f} = U^{T}f\)；逆变换 \(f = U \hat{f}\) 。

传统信号处理 图论 (Graph Theory)
拉普拉斯算子 \(\Delta\) 图的拉普拉斯矩阵 \(\mathbf{L}\)
频率 k 拉普拉斯矩阵的特征值 \(\lambda _{k}\)
傅里叶基 \(exp(-2πixt)\) 拉普拉斯矩阵的特征向量 \(U\)

代入卷积定理得到：

\[ (f * g) = U (U^{T}f \odot U^{T}g) = U K U^{t}f \]

其中 K 是由于哈达玛乘积，推导得到的，是一个对角矩阵；这就是我们需要的卷积核，我们只关心卷积核的学习，因而记 \(g \cdot u_{k} = \theta _{k}\)：

\[ \mathbf{K}=\begin{bmatrix} \mathbf{g}\cdot\mathbf{u}_1&0&\cdots&0\\0&\mathbf{g}\cdot\mathbf{u}_2&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&\mathbf{g}\cdot\mathbf{u}_m \\ \end{bmatrix} = \begin{bmatrix} \theta_1&0&\cdots&0\\0&\theta_2&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&\theta_m \end{bmatrix} \]

GraphSAGE

动机

GraphSAGE 提出的前提是因为基于直推式 (transductive) 学习的图卷积网络无法适应工业界的大多数业务场景。我们知道的是，基于直推式学习的图卷积网络是通过拉普拉斯矩阵直接为图上的每个节点学习 embedding 表示，每次学习是针对于当前图上所有的节点。然而在实际的工业场景中，图中的结构和节点都不可能是固定的，会随着时间的变化而发生改变。在这样的场景中，直推式学习的方法就需要不断的重新训练才能够为新加入的节点学习 embedding，导致在实际场景中无法投入使用。

传统图卷积操作针对的对象是整张图，面对大规模图时难以实现。斯坦福大学提出了一种归纳 (inductive) 学习的 GCN 方法——《Graph Sample and Aggregage:GraphSAGE》，即通过采样 (sample) 和聚合 (aggregate) 邻居信息的方式为给定的节点学习 embedding。不同于直推式 (transductive) 学习，GraphSAGE 是通过学习聚合节点邻居生成节点 Embedding 的函数的方式，为任意节点学习 embedding，进而将 GCN 扩展成归纳学习任务。

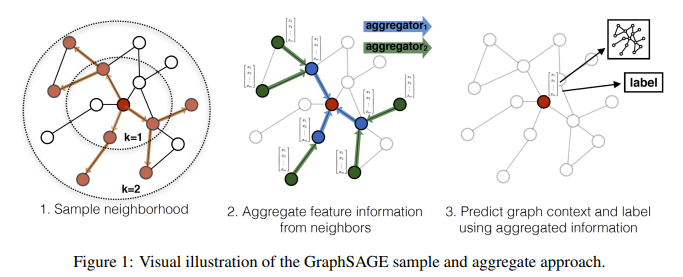
https://raw.githubusercontent.com/darstib/public_imgs/utool/2510/11_251011-151320.png

概览

https://raw.githubusercontent.com/darstib/public_imgs/utool/2509/05_250905-181135.png
GCN overview

这张图找了很久来源，一直觉得可能是哪篇论文的配图（很多文章中使用但是没写来源）最后疑似出自 Food Discovery with Uber Eats: Using Graph Learning to Power Recommendations ；但是好像还是不知道公式是从哪里来的。

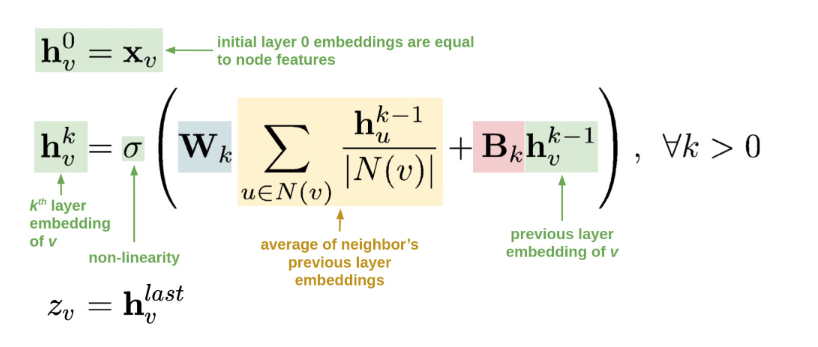
上面是一个 xxx 的算法流程公式解析，核心自然是中间的公式。

  • \(h^{0}_{v}\) 表示节点 v 使用自身的特征 \(\mathbf{x}_{v}\) 初始化的表示
  • \(h_{v}^{k}\) 表示第 k 层卷积后的节点表示，其更新来自两部分：
    • 对 k-1 层得到的邻居表征求平均 (\(\sum_{u\in N(v)}\frac{h_u^{k-1}}{|N(v)|}\))，再进行线性变换 (\(W_{k}\))
    • 对 k-1 层得到的表征 \(h_{v}^{k-1}\) 作线性变换 (\(B_{k}\))
    • 相加后用 sigmoid 函数激活
  • \(z_{v} = h_{v}^{last}\) 表示最后的结果输出
https://raw.githubusercontent.com/darstib/public_imgs/utool/2509/05_1757074885950.png
GraphSAGE algorithm

简而言之，利用采样降低计算复杂度，依据边关系聚合邻居节点信息以及自身信息，作非线性变换。通过多层堆叠，节点能够从全局角度利用到邻居信息；同时 GraphSAGE 支持归纳学习 (inductive learning) ，聚合邻居节点生成 embedding 更适合图结构不断变化的工业场景。

采样

GraphSAGE 的采样过程如下：

  1. 使用一小批节点 B 初始化 \(B^{K}\)
  2. 对于 k 从 \(K\rightarrow 1\) ：
    • 使用 \(B^{k}\) 初始化 \(B^{k-1}\)
    • 以 \(B^{k}\) 中的节点作为中心节点，对邻居进行随机定量采样
      • “随机”使得相似的节点具有相同的表达形式
      • “定量”是为了方便批量训练，每个 batch 等大
      • “采样”是为了避免搜索全图导致计算复杂度高
    • 将采样的邻居加入 \(B^{k-1}\)
  3. 得到 \(\{B^{k}\}_{k\in [K]}\) ，以此为第 k 层卷积操作时需要计算的点。

聚合

由于邻居节点是无序的，所以希望构造的聚合函数具有对称性 ( 即输出的结果不因输入排序的不同而改变 )，同时拥有较强的表达能力。如何对于采样到的节点集进行聚合，介绍的 4 种方式：

  • Mean 聚合：首先会对邻居节点按照element-wise进行均值聚合，然后将当前节点 k-1 层得到特征 \(h_{v}^{k-1}\) ​与邻居节点均值聚合后的特征 \(MEAN(h_{u}^{k}∣u \in N(v))\) 分别送入全连接网络后相加得到结果。
  • Convolutional 聚合：这是一种基于 GCN 聚合方式的变种，首先对邻居节点特征和自身节点特征求均值，得到的聚合特征送入到全连接网络中。与 Mean 不同的是，这里只经过一个全连接层。
  • LSTM 聚合：由于 LSTM 可以捕捉到序列信息，因此相比于 Mean 聚合，这种聚合方式的表达能力更强；但由于 LSTM 对于输入是有序的，因此该方法不具备对称性。作者对于无序的节点进行随机排列以调整 LSTM 所需的有序性。
  • Pooling 聚合：对于邻居节点和中心节点进行一次非线性转化，将结果进行一次基于element-wise的最大池化操作。该种方式具有较强的表达能力的同时还具有对称性。

注意到采样和聚合的顺序时相反的，我们希望信息逐层从边缘向中心节点聚集，最后得到中心节点的表征。

  1. 在一个图中，并不一定每个节点都有监督信号（标签），计算模型损失时只考虑有监督信号的节点。 ↩

评论