Knowledge Graph Embedding¶

参考论文：Knowledge Graph Embedding: A Survey of Approaches and Applications

知识图谱嵌入 (Knowledge Graph Embedding, KGE) 是知识图谱研究的一个子反向，其目标是将知识图谱中的实体和关系嵌入到一个连续的向量空间中，而得到的这些嵌入向量可以被用在很多知识图谱的子任务中，比如知识图谱补全。

基本思路是：

1. 基于观测事实（fact，实体 - 关系 - 实体三元组，一般使用 \(\mathbb{D}^{+}=\{(h, r, t)\}\)）表示实体和关系
2. 学习一个评估函数 \(f_{r}(h, t)\) 来衡量事实的合理性 (Plausibility)（其实可以认为是损失函数）
3. 最大化合理性来更新实体和关系的表示

KG 嵌入的方式根据评估函数的不同可以分成平移距离模型 (Translation Distance Model) 和语义匹配模型 (Semantic Matching Model) 两种形式。

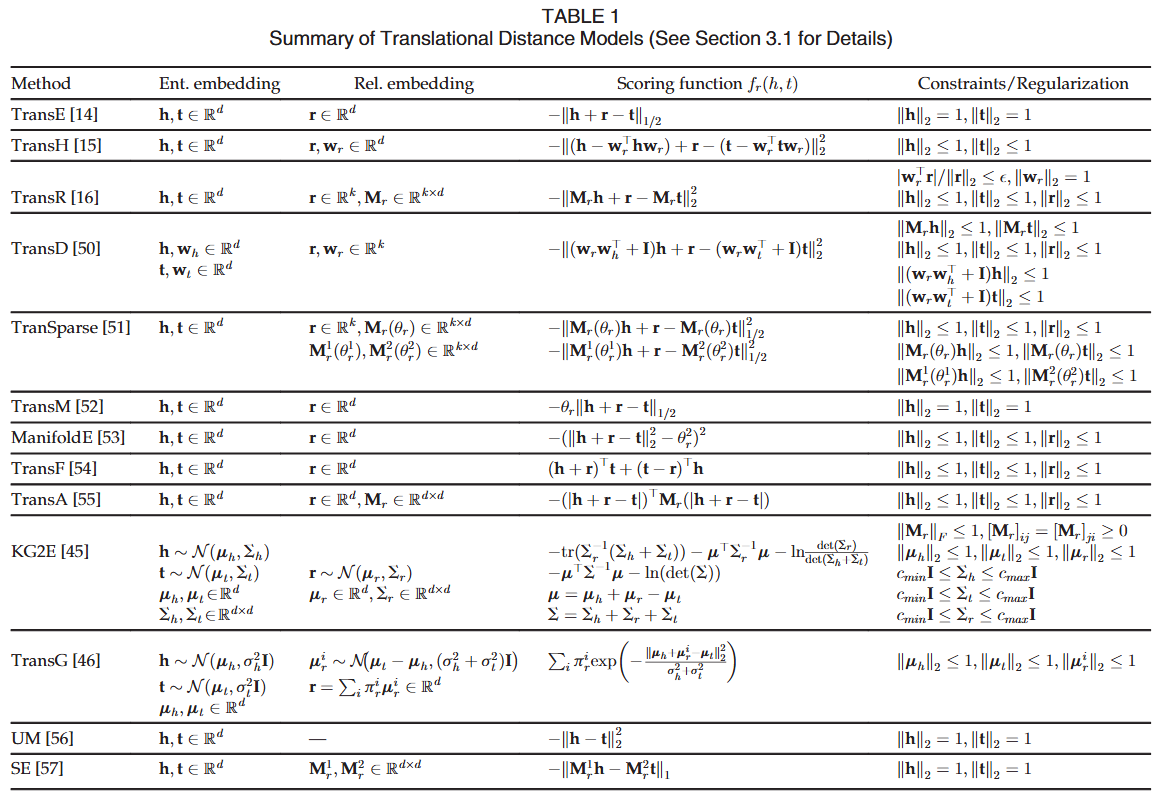
平移距离模型 (TDM) ¶

TDM 利用基于距离的评估函数，这类模型将“关系”视为连接两个实体嵌入向量的一个向量（的平移），即 \(\vec{r} = \vec{t} - \vec{h}\) 。

TransE¶

TransE 是最早也是最著名的平移距离模型（之后也有很多变体，如 TransH, TransR），它将实体和关系都用 d 维空间中的向量来表示，并且希望学习到的嵌入向量满足 \(\vec{r} = \vec{t} - \vec{h}\)，而其评估函数可以表示为（p 一般取 1 或 2）：

TransE 的缺点在于只适合处理一对一的关系，而当知识图谱中出现一对多，多对一，多对多的关系的时候，使用这种算法学习到的嵌入向量的表示能力并不好。

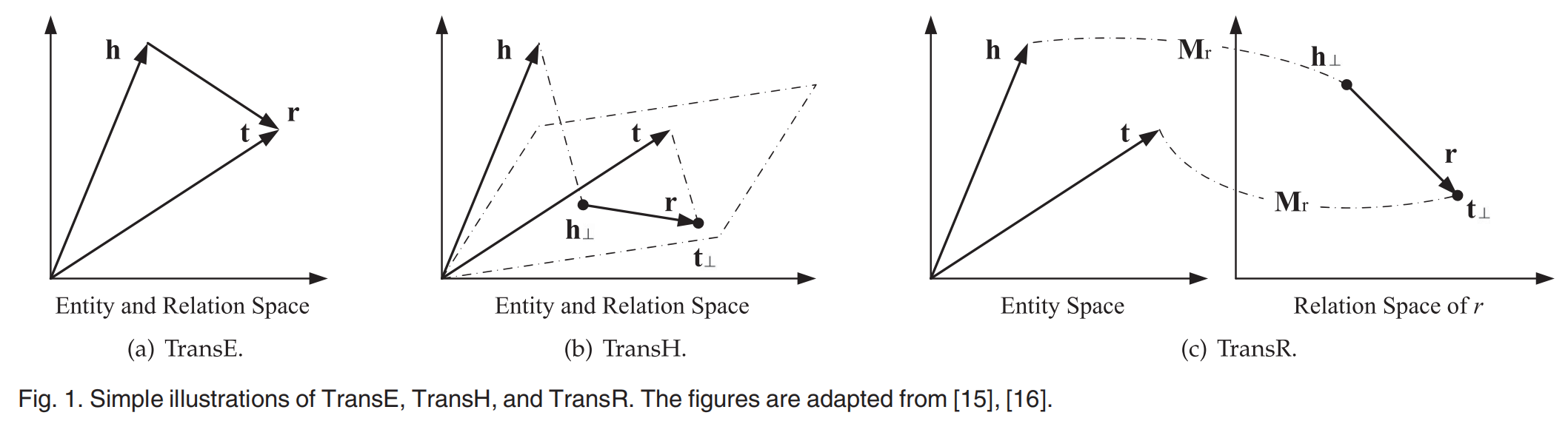
TransH¶

为了解决多元关系上 TransE 的局限性，TransH 提出当实体参与不同的关系时，将其投影嵌入到一个新的空间中。具体而言，为每个关系定义一个超平面（法向量为 \(w_{r}\)），投影公式为（v 代表 h 和 t）：

TransR¶

TransR 则提出为每个关系建立专门的投影空间，使用矩阵 \(M_{r} \in \mathbb{R}^{d\times k}\) 进行线性变换（v 代表 h 和 t）：

TransD¶

由于 TransR 中 \(M_{r}\) 的参数量较大，TransD 通过用三个映射向量 \(w_{h}, w_{r}, w_{t}\) 来构建两个投影矩阵，从而减少参数量：

TranSparse¶

TranSparse 则通过引入稀疏性约束 \(\theta_{r}\) 来控制投影投影矩阵的参数量，具体如下（\(M_{r}(\theta_{r})\) 相同时为共享版本）；

TransM¶

TransM 提出的思路是为每个关系设定一个权重 \(\theta_{r}\)，为一对多，多对一，多对多关系赋予较小的权重，也即减小这些关系对训练的影响（把简单关系做好）：

TransF¶

TransF 则认为只要 r 和 t-h 的反向差不多就行，因此有：

TransA¶

TransA 参考马氏距离，引入了一个新的评估函数（\(M_{r}\) 为对称矩阵）：

通过学习 \(M_{r}\) 来应对复杂的情况。

KG2E¶

KG2E 将每个实体和关系都表示为多元高斯 \(N\left( \mu, \Sigma \right)\)；此时比较的是 \(t-h \sim N(\mu_t-\mu_h,\, \Sigma_t+\Sigma_h)\) 与 \(r \sim N(\mu_r,\, \Sigma_r)\) 两个分布的相似度。

相似度用两类度量计算：

1. KL 散度（Kullback-Leibler Divergence，越小越好）
2. 概率积内核（Probability Product Kernel，越大越好）

TransG¶

TransG 认为一个关系往往是多义的，于是把关系表示为高斯混合 \(r = \sum_i p_i\, \mathcal{N}(\mu^{(i)}_r,\, \sigma^2 I)\)，实体仍用各自的高斯（常取各向同性方差）。打分是对各语义分量的加权求和，本质是对多种“平移” \(h + \mu^{(i)}_r \approx t\) 的指数式相似度求混合；混合分量的数量与权重可用中餐馆过程自适应学习，从数据中自动发现“一个关系的多种语义”。

直观上，Gaussian/ 混合高斯嵌入能更稳健地处理不完备与噪声数据，并刻画关系多义性；代价是参数更多（如协方差、混合分量）与训练计算更复杂。

小结 ¶

语义匹配模型 (SMM) ¶

​SMM 通常使用基于相似度的评估函数，通过计算实体和关系在向量空间中的潜在语义匹配度来评估嵌入向量的合理性。

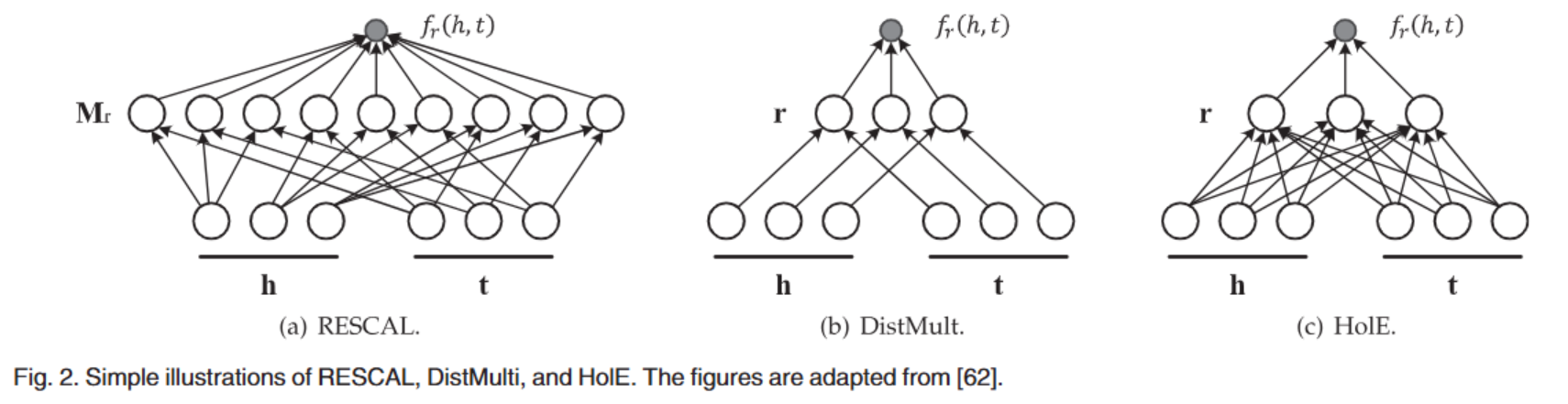
RESCAL¶

RESCAL (a.k.a. the bilinear model) 认为实体用向量表示，关系则直接使用矩阵表示，评估函数是一个双线性函数：

• DistMult 将 \(M_{r}\) 约束为一个对角矩阵，显然这只能够处理对称的关系
  • \(f_r(h,t)=\mathbf{h}^\top\mathrm{diag}(\mathbf{r})\mathbf{t}=\sum_{i=0}^{d-1}[\mathbf{r}]_i\cdot[\mathbf{h}]_i\cdot[\mathbf{t}]_i\)
• HolE 利用循环相关操作提高矩阵的表达能力
  • \(f_r(h,t)=\mathbf{r}^\top(\mathbf{h}\star\mathbf{t})=\sum_{i=0}^{d-1}[\mathbf{r}]_i\sum_{k=0}^{d-1}[\mathbf{h}]_k\cdot[\mathbf{t}]_{(k+i)\operatorname{mod}d}\)
• ConplEx 引入复数一遍更好地对非对称关系进行建模
  • \(f_r(h,t)=\mathrm{Re}\big(\mathbf{h}^\top\mathrm{diag}(\mathbf{r})\overline{\mathbf{t}}\big)=\mathrm{Re}\bigg(\sum_{i=0}^{d-1}[\mathbf{r}]_i\cdot[\mathbf{h}]_i\cdot[\mathbf{t}]_i\bigg)\)
• ANALOGY 在 RESCAL 的基础上对 \(M_{r}\) 添加了约束 (normality, commutativity)
  • \[\begin{aligned}\mathrm{normality:~}&\mathbf{M}_{r}\mathbf{M}_{r}^{\top}=\mathbf{M}_{r}^{\top}\mathbf{M}_{r},\:\forall r\in\mathbb{R};\\\mathrm{commutativity:~}&\mathbf{M}_{r}\mathbf{M}_{r^{\prime}}=\mathbf{M}_{r^{\prime}}\mathbf{M}_{r},\:\forall r,r^{\prime}\in\mathbb{R}.\end{aligned}\]
  • 可以推导（虽然看不懂怎么得到的）将前述四个模型进行统一；也即前述模型都是 ANALOGY 的特例。

NN-based¶

基于神经网络的匹配方法首先将 h,r,t 嵌入为向量（随机初始化、使用 TransE 等方式获得、和网络参数一起学习）。

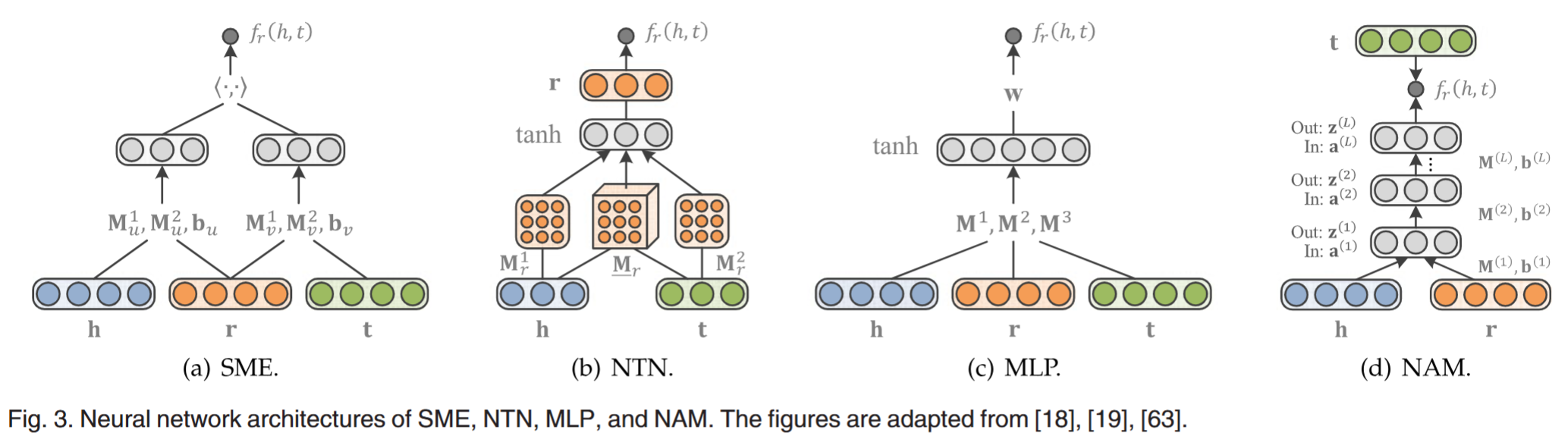
SME¶

语义匹配能量模型 (Semantic Matching Energy, SME) 将实体分别与关系进行线性组合嵌入隐藏层，再计算匹配分数：

• \(g_u(\mathbf{h,r})=\mathbf{M}_u^1\mathbf{h}\oplus\mathbf{M}_u^2\mathbf{r}+\mathbf{b}_u\)
• \(g_v(\mathbf{t,r})=\mathbf{M}_v^1\mathbf{t}\oplus\mathbf{M}_v^2\mathbf{r}+\mathbf{b}_v\)
• \(f_r(h,t)=g_u(\mathbf{h},\mathbf{r})^\top g_v(\mathbf{t},\mathbf{r})\)

其中 \(\oplus\) 可取 \(+, \cdot\)，分别代表了线性组合和双线性组合。

NTN¶

神经张量网络 (Neural Tensor Network, NTN) 评估函数为：

看起来有点像推荐系统中的二阶交叉特征，是本篇涉及的模型中表达能力最强的模型，但是碍于参数过多难以处理大型图谱。

MLP¶

多层感知机 (Multi-Layer Perceptron, MLP) 就是比较存粹的线性组合加非线性激活：

NAM¶

神经关联网络 (Neural Association Model, NAM) 比较简单粗暴，将 h, r 拼接后输入一个 L 层简单神经元构成的网络，将输出与 t 进行匹配：

1. \(\mathbf{z}^{(0)}=[\mathbf{h};\mathbf{r}]\in\mathbb{R}^{2d}\)
   • \(\mathbf{a}^{(\ell)}=\mathbf{M}^{(\ell)}\mathbf{z}^{(\ell-1)}+\mathbf{b}^{(\ell)},\quad\ell=1,\ldots,L\)
   • \(\mathbf{z}^{(\ell)}=\mathrm{ReLU}(\mathbf{a}^{(\ell)}),\quad\ell=1,\ldots,L\)
2. \(f_r(h,t)=\mathbf{t}^\top\mathbf{z}^{(L)}\)

应用 (application) ¶

In-KG¶

链接预测 (Link prediction) ¶

链接预测任务一般指预测两个实体之间是否存在特定关系，常见的做法是给定 h/t 和 r，所有的 t/h 作为候选答案进行选择；也可以给定 h 和 t，寻找 r。

以寻找 t 为例，为了方便训练和评估（以及类比推荐系统和语言生成模型），更一般的做法是依据 h 和 r ，将候选的所有 t 进行排序，随后进行评估（已经有很多对排序结果进行评估的方法了，例如 Hits@n , AUC-PR）。

三元组分类 (Triple Classification)¶

一般指判断事实三元组 (h, r, t) 的真假性；简答的形式是为合理性 \(f_{r}(h, t)\) 设置一个阈值 \(\delta\)，高于 \(\delta\) 才认为这个事实为真。

实体分类 (Entity Classification) ¶

实体解析一般指判断两个实体是否有所属关系，例如“浅碎时光”是“大学生”。一个简单的方法是定义一个关系 isA 表示两个实体所属，随后就是对 (x, isA, ?) 进行来链接预测了。

实体解析 (Entity Resolution) ¶

实体解析一般指判断两个实体是否指的是同一个对象，例如浙大和浙江大学两个实体实际上是同一个对象。一个简单的方法是定义一个关系 \(equalTo\) 表示两个实体相同，随后就是对 (x, equalTo, y) 进行三元组分类了。

Out-KG¶

关系抽取 (Relation Extraction) ¶

关系抽取的目的是从已经检测到实体的纯文本中抽取关系事实。传统的思路中利用“远程监督”：将已有 KG 上的事实对齐到语料库中包含同一对实体的片段中，用这些片段来训练一个 text-based extractor。这里 KG 只是用于生成训练数据，没有利用到 KG 自身的推理能力。

因此 Weston 等人提出训练 text-based extractor 的同时训练一个 KG 上的 embedding model（如 TransE）来作为辅助，具体融合思路为：

1. 利用 text-based extractor 对文本片段 m 与所有候选关系 r 匹配打分记为 \(S_{text}(m, r)\)，并选出预测关系 \(\hat{r}\)；
2. 利用 embedding model 对三元组 \((h, \hat{r}, t)\) 的合理性进行评分记为 \(S_{KG}(h, \hat{r}, t)\)
3. 复合打分为：\(S_{\mathrm{text}+\mathrm{KG}}(h,\hat{r},t)\:=\:\sum_{m\in M_{h,t}}S_{\mathrm{text}}(m,\hat{r})\:+\:S_{\mathrm{KG}}(h,\hat{r},t)\)

其中 \(M_{h, t}\) 为语料库中所有涉及 h, t 两个实体的片段。直观来说就是：这段文本“像是”在说这俩个实体存在某种关系，且在 KG 里面也“比较合理”，那么这个关系就会被认可。

Riedel 等人提出了另一种结合文本和 KG 的框架，他们构建了一个矩阵：

• 每一行表示一对实体 (h, t)；
• 每一列表示一种关系标记，被分为两部分：
  • 文本提及 (Textual mentions)
    • "directed by", "made by" 等表示所属关系的文本片段
  • 知识图谱关系 (KG relations)
    • "DirectedOf", "ActorIn" 等规范化的关系

当一个实体对在语料库中或者知识图谱中以对应关系标记被提及 / 存在时，则标记对应单元为 1，否则为 0；对于测试样例即补全图中 ? 区域的标记情况。

问答系统（Question Answering）¶

给定一个用自然语言表达的问题，任务是从 KG 中检索由三元组或三元组支持的正确答案。一个可行的方法是学习单词和 KG 成分的低维向量嵌入，使问题的表示和相应的答案在嵌入空间中相互接近，进行检索召回。

推荐系统（Recommender Systems）¶

有学者提出了一种混合推荐框架，该框架利用 KG 内的异构信息来提高协同过滤的质量——使用存储在 KG 的三种类型的信息 , 包括结构性知识 ( 事实三元组 ), 文本知识 ( 例如 , 一本书或一部电影的文本性的总结 ), 和视觉知识 ( 例如 , 一本书的封面或电影海报图片 ), 为每项生成语义表示。

如果这对你有用的话，请给我点个star吧 ===>