介绍 ¶
演进趋势 ¶
在 YoutubeDNN 中第一次提出现在主流推荐系统系统的雏形:召回 + 排序
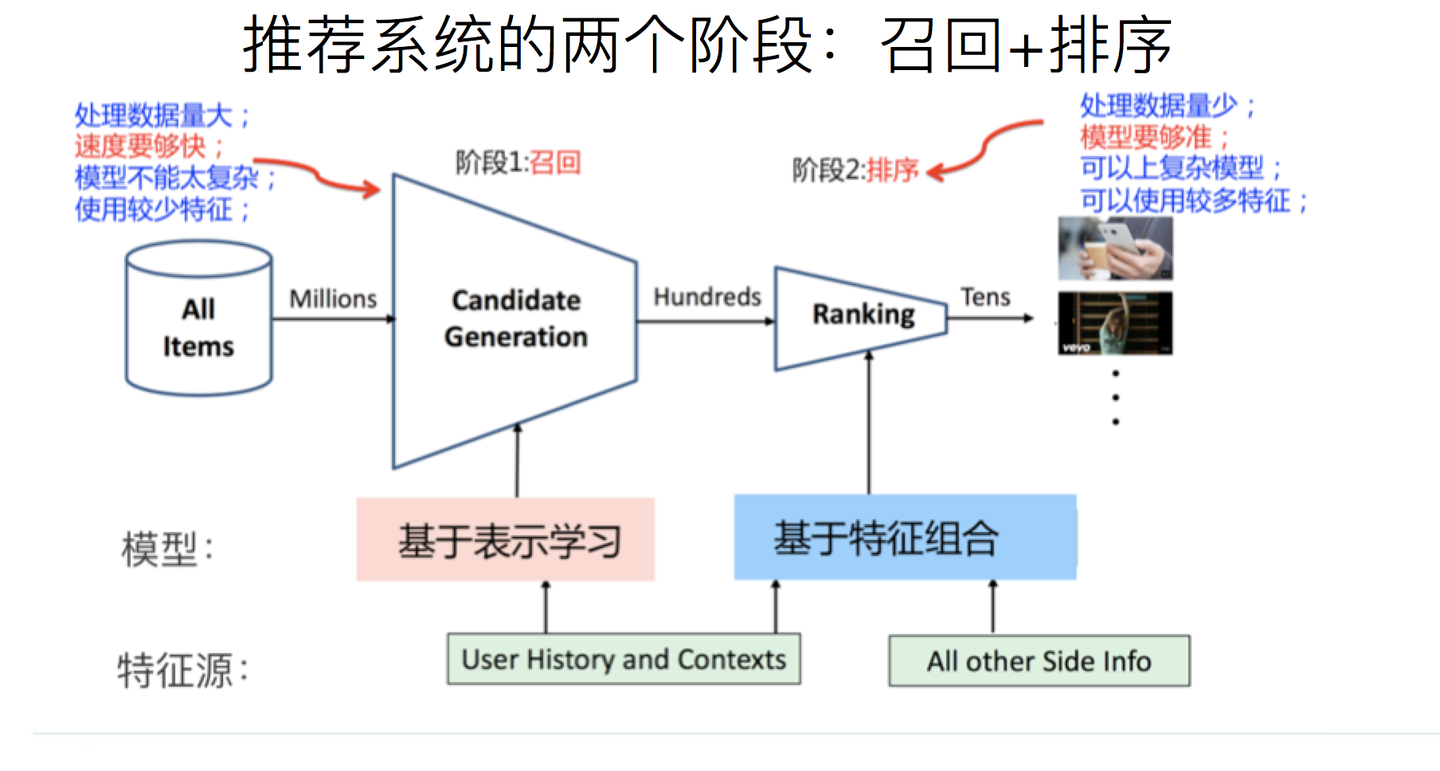
召回阶段从海量物品中找到用户感兴趣的那一批;排序阶段从一批可能感兴趣的物品中找到最感兴趣的内容向用户推送。随着物品池中物品数量暴增,更加细致的筛选架构被设计以权衡速度和质量。
在部分业务情境下,YoutubeDNN 给出的架构仍然被使用。
YoutubeDNN¶
基于论文 Deep Neural Networks for YouTube Recommendations
这篇文章放在这是因为其架构非常经典,但并不是说下面的内容都是出自这篇文章,有后续补充内容;
有些地方可能比较跳脱,可以之后再回顾。
YouTube 是一个规模庞大、以视频为主(物品新颖度要求高
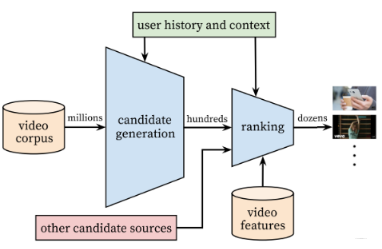
从架构上看,从视频池 (video corpus) 中取出百万级数量的视频,经过 Candidate generation 结构(即现在的召回)筛选出数百视频,经过 ranking 结构(即现在的排序)基于视频特征进行排序,选出一部分向用户进行推送。通过这两个阶段从海量的视频中选择与用户个性化最符合的少量视频向用户进行推荐。
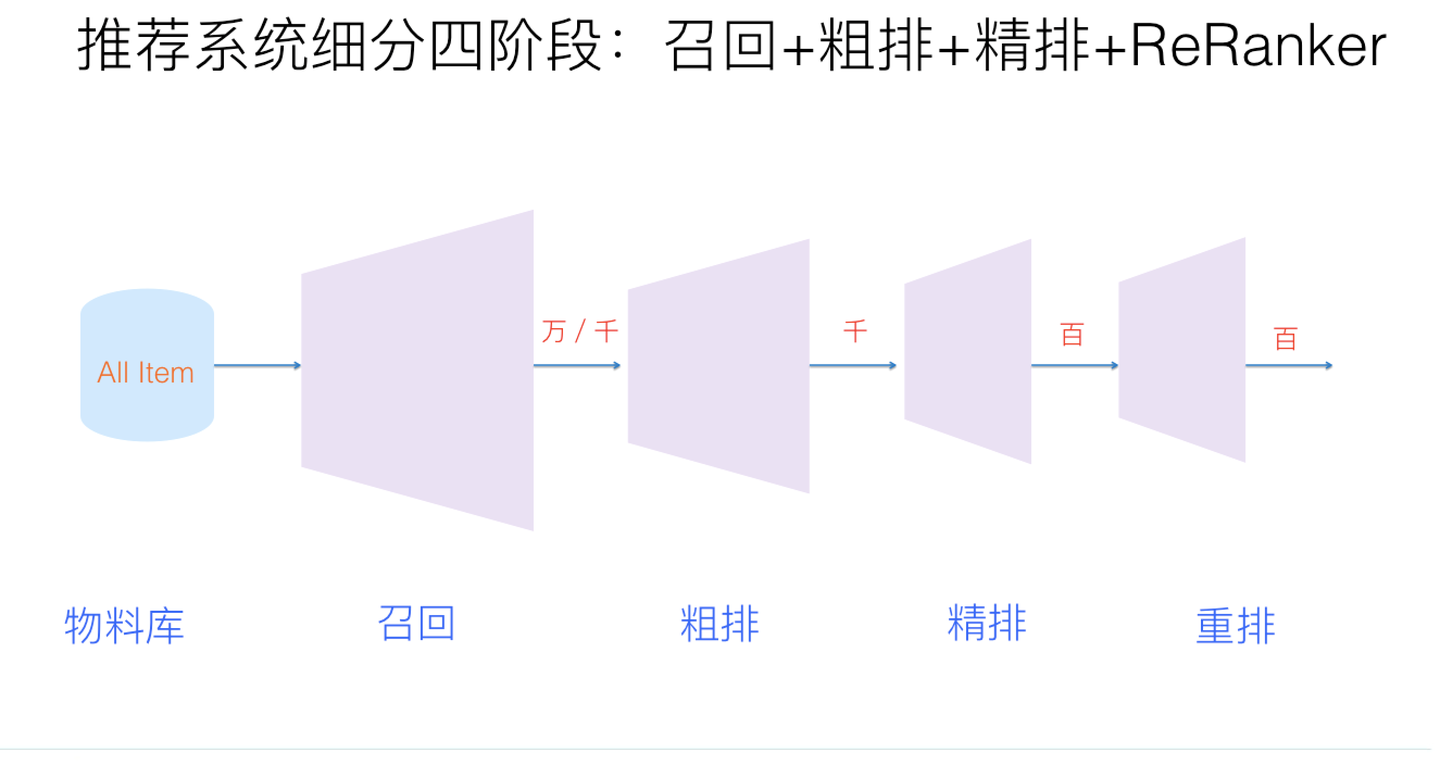
pre-rank & rerank
随着视频数量的增加,一次排序不能够在时间开销和准确度上取得较好的平衡;现在的推荐系统架构在现有排序的前后引入粗排 (pre-rank) 和重排 (rerank) ,并将现有 ranking 阶段称为精排。所以如今的漏斗变得更长了,但是可以方向架构上基本一致。
出于方便,下面以“召回”和“排序”来表示图中的 "candidate generation" & "ranking" 部分。
召回 ¶
回顾召回的目的:从海量物品中找出用户可能感兴趣的一批物品。而论文中使用 generation 这个词不是没有原因的;YoutubeDNN 将寻找用户可能感兴趣的物品视为 “generate next video” 任务(也即多分类任务
如下图所示,基于 Word2vec,预先将观看记录和搜索记录嵌入向量库;由于记录是一个序列,使用 average pooling (逐维取平均)转变为一个向量。结合地理特征和其他信息的向量进行拼接 (concat),经过多个以 ReLU 为激活函数的全连接层构成的 DNN(最后一个 ReLU 层输出视为用户向量)和 Softmax 激活的全连接层(softmax 的输入实际是 user-vector 与 video vector 的内积,这与 Skip-gram(SG) 是类似的进行训练 (training),所以全连接层的 W 其实就是 item 向量构成的矩阵) 后,我们可以得到对“用户将要观看下一个视频的概率”的预估:
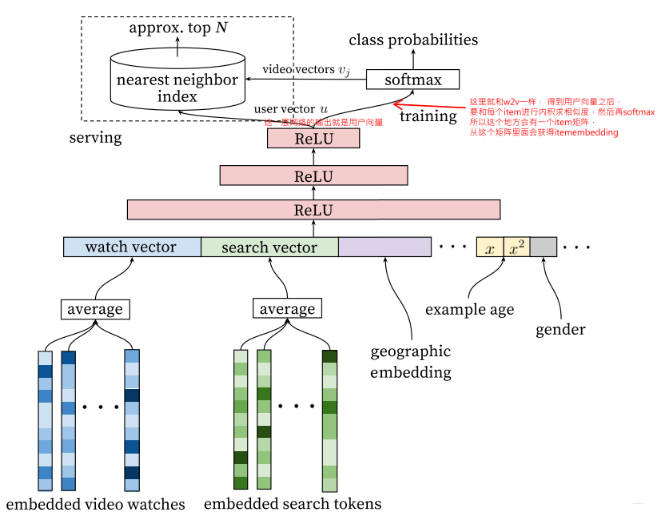
也可以表述为,在时刻 t 下,用户 U 将要观看视频 \(i \in V\) 的概率为
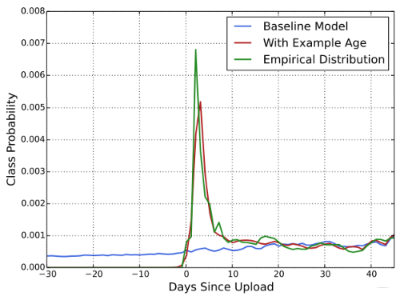
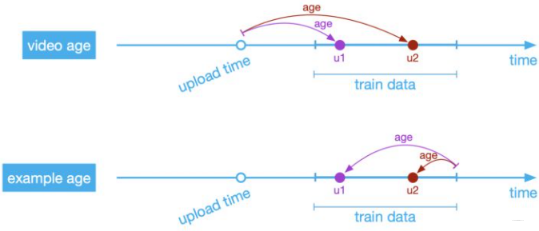
example age
注意到嵌入向量中有一个 example age,其与实际业务场景相关。在实际场景中,一个新上传的视频可能对用户有更高的点击欲望,即在上传初期能够有更好看的数据;而 average pooling 只是记录序列的一个平均,不能够体现这一点。
记 t 为数据被采样的时间,example age 定义为训练数据中最晚被采样的样本的时间减去当前样本的采样时间;过去使用的是 video age,区别如下:
example age 的好处在于:
- 线上预测时所有 item 的该项统一
- 便于归一化操作
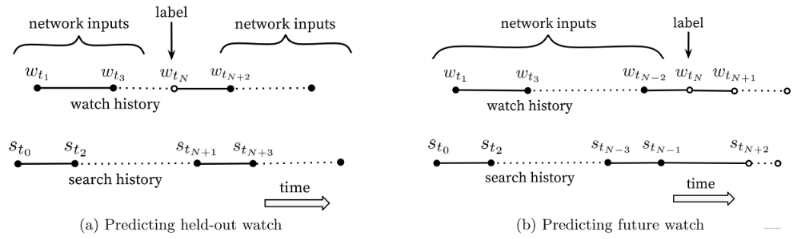
论文中还将历史搜索记录序列打乱,如果使用 average pooling 似乎没区别?
而对于历史观看记录,在获取样本时,对于历史记录等较少的新用户,论文中利用较小的滑动窗口预测下一个。例如实际序列为 abcdefg,那么提供 abc 预测 d、提供 bcd 预测 e …… 这也依据于结合数据分析发现用户行为的非对称观看概率 (asymmetric co-watch probabilities)——用户往往先较为广泛地观看,之后专注于较小的范围(从探索到深入
负采样 ¶
不同于 token-generation,词表的大小一般只有几万,而视频的数量是几百万甚至更多,softmax 的开销将会非常大。为此使用一些方法进行优化,一般使用负采样。需要注意的是每个用户的负样本数量保持相同以避免某一用户对训练造成明显影响。
推荐系统中,负样本采样技术:推荐系统正负样本的划分和采样,如何做更合理?
In-Batch 负采样认为在一个 batch (即一组用户 - 物品对)中,用户对自己物品较感兴趣,而对起他人的物品不太感兴趣(作为负样本
全局随机采样负样本(Word2vec 中的负采样)
基于极大似然估计和贝叶斯假设,我们可以推导得到随机负采样的下的损失函数为:
其中 \(\sigma(x) = \frac{1}{1 + e^{-x}}\) 表示 sigmoid 函数,K 是采样的负样本集合;这个损失函数不仅希望最大化中心词和周边词的相似度 (\(u_o^T v_c\)),同时最小化负样本(追求简单时直接随机从字典中采样,我们认为它们大概率与中心词无关)与中心词的相似度,而避免计算词典中所有词。
随机采样 + 热门打压:对于巨大的物品库,其中特定用户感兴趣的只是其中的一小部分,随机从物品库中抽取的物品往往用户不喜欢。 在实际业务中,热门物品(高点击)物品往往只占据了物品库的很小一部分(长尾效应),随机抽样很可能导致负样本大多是冷门物品,致使冷门物品更加难以被推荐,加剧长尾效应。 因而在负样本采样时我们期望以更大概率采样热门物品以进行适当打压控制流量。业界一般使用 \(P^{neg}_{i}=\frac{n(w_i)^\alpha}{\sum_jn(w_j)^\alpha}\) 作为物品被采样为负样本概率,其中 \(n(w_{i})\) 表示物品 i 的点击次数,\(\alpha\) 为超参数(一般取 0.75)。
纠偏
在训练时,为了避免长尾物品过于冷门,可以使用物品被抽样的概率对相似度进行打压;即越热门的物品抽样概率越高,越应该适当降低被推荐概率以提高长尾物品的曝光率;例如将 \(u_i v_i\) 替换为 \(u_i v_i - \log p_{j}\),其中 \(p_{j}\) 与物品被点击率正相关。
为什么是 \(-\log p_{j}\) ?在上面我们使用到 exp,而 \(e^{(u_{i}v_{i}-\log p_i)} = e^{u_{i}v_{i}}/p_{j}\) ,所以本质是为了符合 softmax 中 exp 的情况下对权重进行一个放缩。
直观而言我们期望模型学习到用户真正的偏好,而非因视频热门导致的用户点击行为。
流频估计算法是适用于几乎时刻收到新物品的平台(尤其是 UGC 平台)动态获取和维护 \(p_{j}\) 的算法,其核心实现在于用采样频率来估计采样概率。如果一个物品的采样频率为 k,那么采样概率为 \(\frac{1}{k}\)。
- 构建哈希函数 \(h(\cdot)\),能够将物品 (ID) 映射到 [H] 这 H 个数字构成的列表中
- 记录物品的采样时间信息;物品在实时更新,我们不可能使用一个无限大的列表
- 出现哈希冲突时,可能会预估物品采样频率过高,可以使用多重哈希减少误判
- 建立两个大小为 H 的数组 A, B
- \(A[h(y)]\) 保存物品 y 上一次被采样的时间步
- \(B[h(y)]\) 保存物品 y 的“全局步长”
- 如果在时间步 t 采样到物品 y,更新:
- \(B[h(y)]\leftarrow(1-\alpha)\cdot B[h(y)]+\alpha\cdot(t-A[h(y)])\)
- \(A[h(y)] \leftarrow t\),上面的 \(\alpha\) 是学习率
- batch 采样结束,记 \(\hat{p} = 1 / B[h(y)]\)
排序 ¶
论文后面还提到了排序部分,但如今排序模型已经是迭代得很厉害了,不再展开。