Graph-based¶

一般而言，我们说的基于图的召回是依据图嵌入学习物品 / 用户的嵌入表示，之后使用 ANN 等技术进行召回。

Enhanced Graph Embedding with Side information (EGES)¶

参考阿里巴巴在 2018 年的 KDD 上提出的论文： Billion-scale Commodity Embedding for E-commerce Recommendation in Alibaba

动机 ¶

基于协同过滤、基于内容和深度学习的已有方法在小规模物品集上表现良好，但在数以亿记得大规模物品集上表现较差
由于物品集数量庞大，用户 - 物品交互矩阵稀疏
冷启动问题

引入 Graph Embedding 以尝试解决这些问题；论文中使用的是 DeepWalk 并进行了一些改进，共提出了三种嵌入方法：BGE, GES, EGES 。

构建物品图 ¶

进行图嵌入之前，我们首先需要有一个图，出于物品相对更加稳定我们构建 Item-item graph。基于 ItemCF 的物品嵌入只考虑了物品的共现属性而丢弃了顺序信息（而用户的浏览是有顺序的），顺序信息可以更好地反映用户偏好，故记录用户的行为序列。考虑到：

序列过长将导致时间和空间成本增加
用户兴趣随时间变化较快，较早序列信息可能意义不大

可以使用一个（基于时间 / 数量）的窗口并仅考虑窗口内的行为序列，记作一个会话 (session) 。基于行为序列，我们构建一个有向有权图：方向为连续访问的两个物品之间的顺序，权重为重复连接次数。换句话说，边 \(e_{ij}\) 代表了从物品 i 移动到物品 j 的频率来表征物品间的相似度。

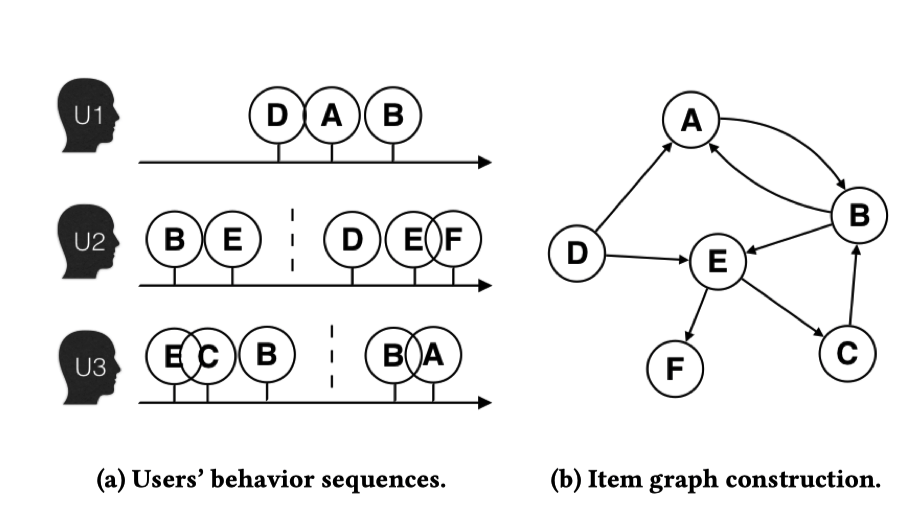
https://raw.githubusercontent.com/darstib/public_imgs/utool/2509/04_1756982827374.png — Item-item graph build

噪声过滤

对于较为“异常”的行为应该进行清理过滤：

停留时间过短（如 1 s）应该删除，说明不感兴趣或是误操作
“过于活跃的用户”，有可能就是机器人或爬虫
检查物品标识符与实际物品的匹配情况（可能物品更新了非常多）

Base Garph Embedding (BGE)¶

考虑可扩展性的问题，图嵌入的随机游走方式可以在物品图上捕获物品之间高阶相似性，即 Base Graph Embedding（BGE）方法。其不同于 CF 方法，除了考虑物品的共现，还考虑到了行为的序列信息。

如前所述，DeepWalk 的思路即

随机游走获得物品序列
基于 skip-gram 生成 embedding

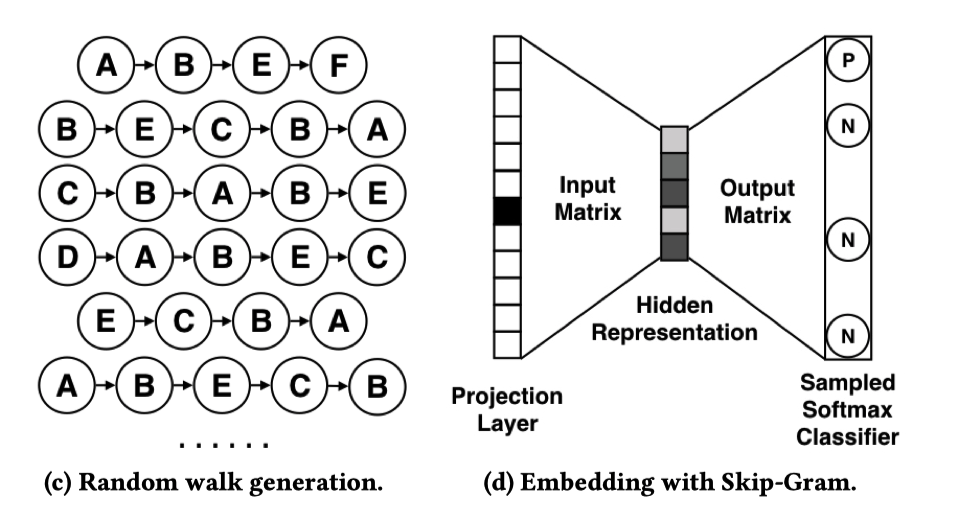
https://raw.githubusercontent.com/darstib/public_imgs/utool/2509/04_1756995929431.png — random walk + skip-gram

论文中将随机游走换为带权游走策略，（接近于 node2vec），给定图的邻接矩阵，得到游走的转移概率为：

\[ P(v_j|v_i)=\begin{cases}\frac{\mathbf{M}_{ij}}{\sum\limits_{j \in N_+(v_i)}\mathbf{M}_{ij}},&\quad v_j\in N_+(v_i)\:,\\0\:,&\quad e_{ij}\notin\mathcal{E}\:,\end{cases} \]

其中 \(M_{ij}\) 是有向边 \(e_{ij}\) 的权重，\(N_{+}(v_{i})\) 是所有 i 的出度邻居（如果定义没有 \(i \rightarrow j\) 的边则权重为 0，那么 \(j \neq i\) 即可）。获得节点序列，极大似然估计 => 极小负对数似然：

\[ \underset{\Phi}{\operatorname*{minimize}}-\log Pr\big(\{v_{i-w},\cdots,v_{i+w}\}\backslash v_i|\Phi(v_i)\big) \]

同样基于贝叶斯假设和负采样得到（\(N(v_{i})'\) 是负样本集合）：

\[ \text{minimize}\log\sigma(\Phi(v_j)^T\Phi(v_i))+\sum_{t\in N(v_i)^{\prime}}\log\sigma(-\Phi(v_i)^T\Phi(v_i)) \]

Attention

上面是论文中的公式，但是结合 skip-gram 中的损失函数可以发现整个最小化的内容应该添加一个负号（或者是最大化该公式），询问 GPT-5/Gemini-2.5-pro/Claude-Opus-4.1 都认为确实存在问题。

Graph Embedding with Side information¶

BGE 解决了节点怎么嵌入的问题，但是对于新加入、没有交互信息的物品呢？即仍然是冷启动问题。考虑到稀疏性和冷启物品问题，在图嵌入的基础上，考虑了节点的属性信息。希望具有相似属性的物品可以在空间上相似，即希望通过头部物品，提高属性信息的泛化能力，进而帮助尾部和冷启物品获取更加准确的 embedding，即 Graph Embedding with Side Information（GES）方法。

在电子商务中的推荐系统背景下，辅助信息 (side information) 指的是物品的类别、店铺、价格等，这些信息在排序阶段被广泛用作关键特征，但在匹配阶段很少被应用。论文中假设具有相似辅助信息的物品在嵌入空间中应该也相近。

使用 \(W\) 表示物品和辅助信息嵌入矩阵，\(W_{v}^{0}\) 表示物品 \(v\) 的嵌入向量，\(W_{v}^{s}\) 表示物品 \(v\) 的第 s 个辅助信息的嵌入向量。对于有 n 个辅助信息的物品，若 \(W_{v}^{i} \in \mathbb{R}^{d}, i \in [n+1]\)，则 \(W \in \mathbb{R}^{d \times(n+1)}\)。

将所有 \(W_{v}^{i}\) 拼接作为输入向量，Skip-gram 的 Input Matrix 换为 Average pooling （即 \(H_{v} = \text{AvgPool}(W) = \frac{1}{n+1} \sum_{s=0}^{n}W_{v}^{s}\)），训练 Ouput Matrix 即可，网络如下：

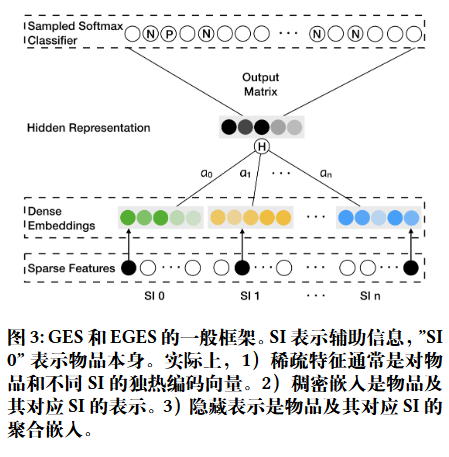
https://raw.githubusercontent.com/darstib/public_imgs/utool/2509/04_250904-222937.png — Arch of GES & EGES

Enhanced Graph Embedding with Side information¶

在求平均时，我们无疑将所有辅助信息一视同仁，而则显然不是那么合理。考虑到不同属性信息对于学习 embedding 的贡献不同，因此在聚合不同的属性信息时，动态的学习不同属性对于学习节点的 embedding 所参与的重要性权重，即 Enhanced Graph Embedding with Side Information（EGES）。用 \(a_{v}^{i}\) 表示 \(W_{v}^{i}\) 的权重，对辅助信息进行加权求和得：

\[ \mathrm{H}_v=\frac{\sum_{j=0}^ne^{a_v^j}\mathrm{W}_v^j}{\sum_{j=0}^ne^{a_v^j}} \]

对标签求交叉熵损失得：

\[ \mathcal{L}(v,u,y)=-[ylog(\sigma(\mathrm{H}_{v}^{T}\mathrm{Z}_{u}))+(1-y)log(1-\sigma(\mathrm{H}_{v}^{T}\mathrm{Z}_{u}))] \]

求梯度得：

\[ \begin{aligned}\frac{\partial\mathcal{L}}{\partial a_{v}^{s}}&=\frac{\partial\mathcal{L}}{\partial\mathcal{H}_{v}}\frac{\partial\mathcal{H}_{v}}{\partial a_{v}^{s}}=(\sigma(\mathrm{H}_{v}^{T}\mathrm{Z}_{u})-y)\mathrm{Z}_{u}\frac{(\sum_{j=0}^{n}e^{a_{v}^{j}})e^{a_{v}^{s}}\mathrm{W}_{v}^{s}-e^{a_{v}^{s}}\sum_{j=0}^{n}e^{a_{v}^{j}}\mathrm{W}_{v}^{j}}{(\sum_{j=0}^{n}e^{a_{v}^{j}})^{2}}\end{aligned} \]

\[ \begin{aligned}\frac{\partial\mathcal{L}}{\partial\mathbf{W}_{v}^{s}}&=\frac{\partial\mathcal{L}}{\partial\mathrm{H}_{v}}\frac{\partial\mathrm{H}_{v}}{\partial\mathrm{W}_{v}^{s}}=\frac{e^{a_{v}^{s}}}{\sum_{j=0}^{n}e^{a_{v}^{j}}}(\sigma(\mathrm{H}_{v}^{T}\mathrm{Z}_{u})-y)\mathrm{Z}_{u}\end{aligned} \]

PinSAGE¶

PinSAGE 模型是 Pinterest 在 GraphSAGE 的基础上实现的可以应用于实际工业场景的召回算法。

Pinterest 公司的主要业务是采用瀑布流的形式向用户展现图片，无需用户翻页，新的图片会自动加载。因此在 Pinterest 网站上，有大量的图片 ( 被称为 pins)，而用户可以将喜欢的图片分类，即将 pins 钉在画板 boards 上。可以发现基于这样的场景，pin 相当于普通推荐场景中 item，用户钉的行为可以认为是用于的交互行为。

于是 PinSAGE 模型主要应用的思路是，基于 pins-boards 二分图，利用 GraphSAGE 的原理学习到聚合方法，并为每个图片 (pin) 学习一个向量表示，然后基于 pin 的向量表示做 item2item 的召回。

重要性采样 ¶

没太看懂，看描述是基于 random-walk 为邻居分配权重，然后按权重进行重要性采样。

聚合算法 ¶

PinSAGE 使用 Convolve 算法（单层图卷积）进行聚合：

https://raw.githubusercontent.com/darstib/public_imgs/utool/2509/05_1757076933873.png — Convolve algo

三步走：

聚合邻居：对邻居节点的表征进行一次线性变换和一次非线性变换，最后使用对称向量函数 (symmetric vector function \(\gamma(\cdot)\)) 进行 pooling 聚合得到邻居表征 \(n_{u}\)
节点更新：将当前节点表征 \(z_{u}\) 与 \(n_{u}\) 拼接，经过一次线性变换和非线性变换得到新的节点表征 \(z_{u}^{NEW}\)
节点表征归一化操作，有利于近似最近邻 (ANN) 搜索

Symmetric function & pooling

对称函数 ( Symmetric function )

In mathematics, a function of n variables is symmetric if its value is the same no matter the order of its arguments.

顾名思义，对称函数是结果与一串输入顺序无关的函数，包括但不限于求和、求平均、取最大值等。

池化 (Pooling) 操作是卷积神经网络 (CNN) 中的重要一环，本质是信息过滤、降维采样，对于来自卷积层等的输入使用对称函数处理。详细可参考：卷积神经网络中的池化 (Pooling) 层

基于 mini-batch 多层图卷积 ¶

与 GraphSAGE 一样基于 mini-batch 堆叠多层图卷积层来逐层聚合信息。训练时使用 Margin Hinge Loss 损失函数：

\[ J_{\mathcal{G}}(\mathbf{z}_{q}\mathbf{z}_{i})=\mathbb{E}_{n_{k}\sim P_{n}(q)}\max\{0,\mathbf{z}_{q}\cdot\mathbf{z}_{n_{k}}-\mathbf{z}_{q}\cdot\mathbf{z}_{i}+\Delta\} \]