Sequence-based¶

LastN¶

LastN 即关注用户最后交互的 N 的物品，作为一个新的用户特征。最简单的思路是，将用户最后交互（点击、点赞、转发）的物品进行嵌入（依据物品 ID，也可以结合物品本身属性）得到嵌入向量。最简单的，对这 N 个嵌入向量求平均得到新的用户特征向量。

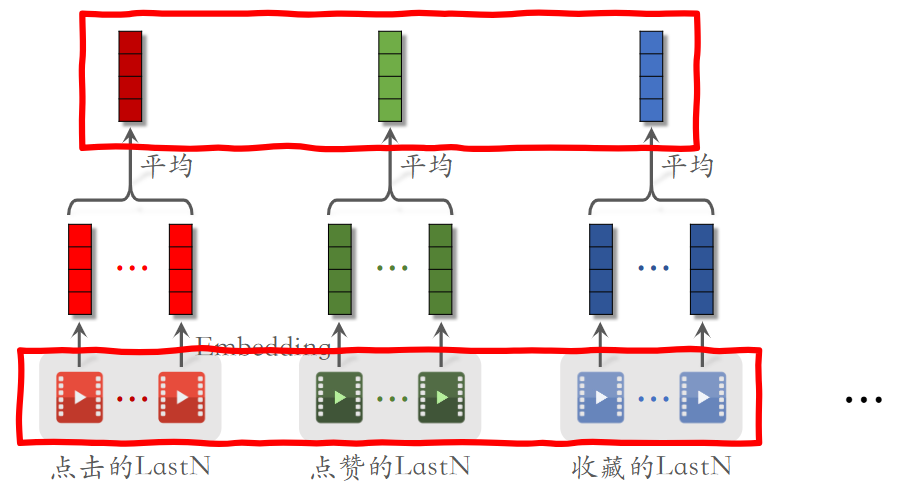
但这无疑丢失了用户 LastN 中的“序列”信息，我们期望通过用户的历史行为序列去学习用户的特征和兴趣。

基于 Word2vec/Item2vec 的思路，我们将推荐问题转变为序列预测问题，就像语言模型预测下一个词一样；如果序列过长，基于注意力机制 / 长短期分离 / 多兴趣表征都是较好的优化手段。

Deep Interest Network (DIN)¶

DIN 用加权平均（注意力机制）代替平均求和；权重（注意力）取决于候选物品与用户 LastN 物品的相似度。

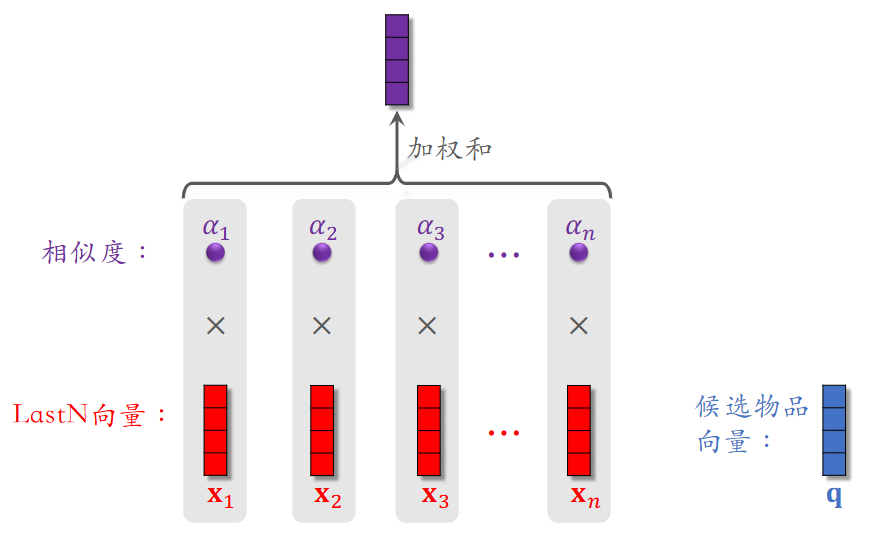
其本质参考了注意力机制（DIN 由阿里在 2018 年提出）

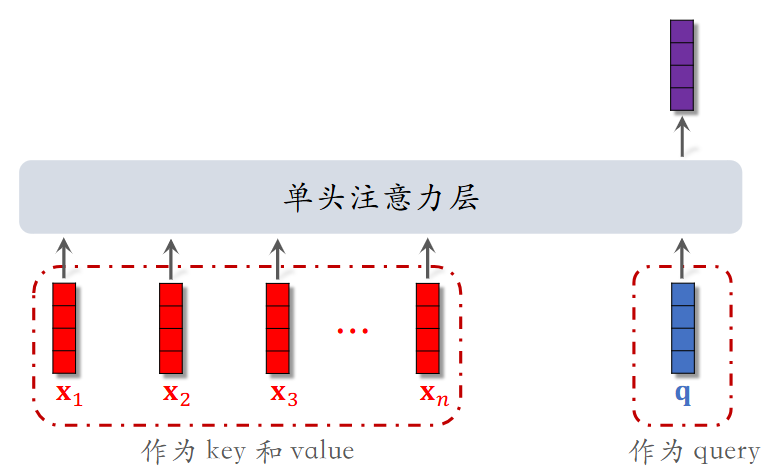
DIN 需要能够在处理用户特征时看到物品特征，所以不适合召回（双塔模型）和粗排（三塔模型），适合在精排阶段使用。

Search-based user Interest Modeling (SIM)¶

基于我们之前讨论过的最近邻向量查找（在此称为 Soft Search；也可以简单地依据类别等标签进行查找，称为 Hard Search），我们可以在 LastN 的 N 个物品中找到 TopK 与候选物品相似的物品，保留了长期兴趣的同时减少了模型计算量。

在使用注意力机制时，SIM 为了表征序列信息（保留长序列交互信息），将用户与物品最后一次交互的时间距 \(\delta\) 也嵌入为向量并与物品向量拼接。实验结果表明效果确实更佳。

Tree-based Deep Model (TDM)¶

深度树模型 (TDM) 是基于树结构、将对全量商品检索复杂度 \(O(N) \rightarrow O(\log N)\) 的一个模型。树的基本结构是：叶子节点表示一个商品 item，非叶子节点表示 item 集合，其子节点是该节点的子集。

整体架构如下（可以发现和 DIN 中的非常像，主要区别在于右下角）：

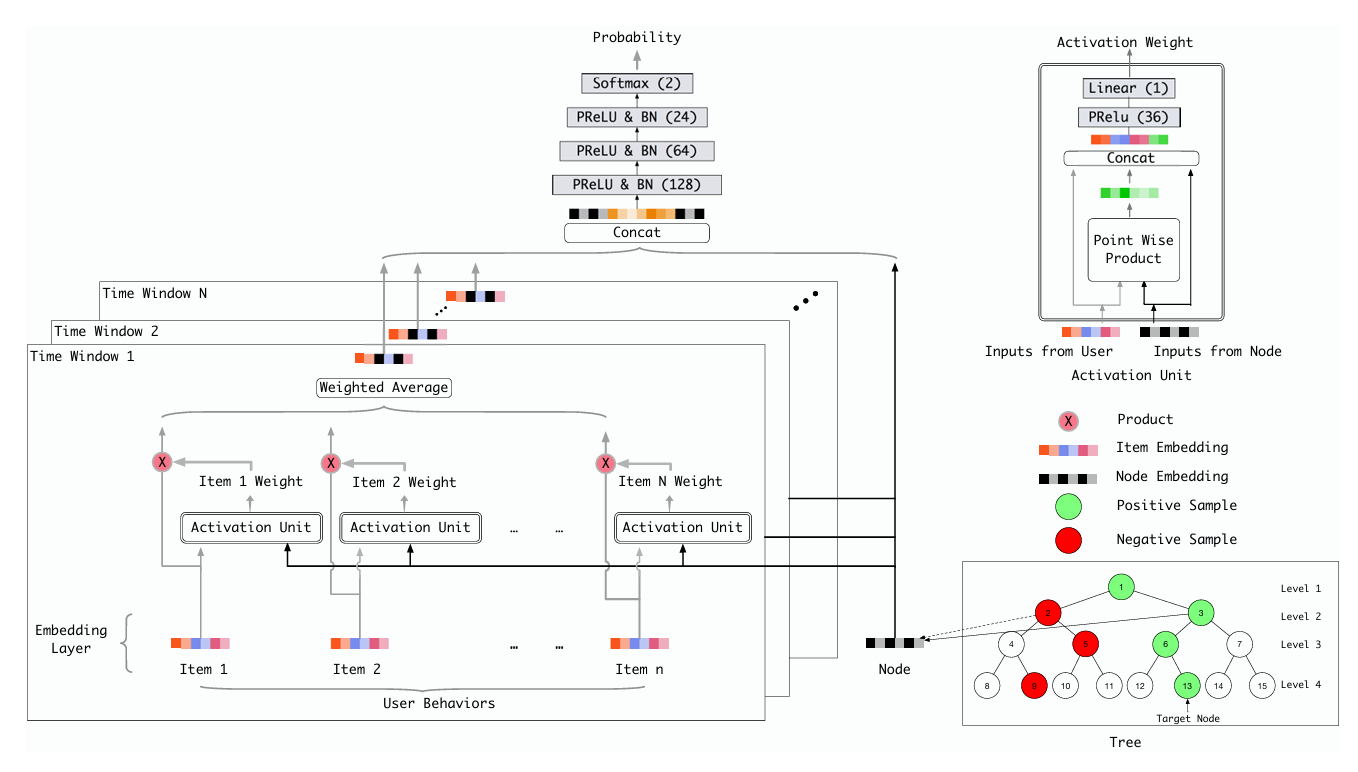
高效检索 ¶

算法上通常采用 Beam-Search，即依次对每层节点选出 TopK 作为下一层的候选集，当前层的 TopK 一定属于上一层的 TopK，最后到叶节点（\(p^{(j)}(n \mid u)\) 表示用户 u 对 j 层节点 n 感兴趣的概率，\(\alpha^{j}\) 为归一化因子）

兴趣建模 ¶

假设现在表现出对 13 号节点感兴趣（如上图右下角），那么沿着路径到根节点都可以认为感兴趣，路线上同城的兄弟节点可以认为作负样本。

其他部分都较为常规，不再细写了。

Multi-Interest Network with Dynamic routing (MIND)¶

MIND 是 CIKM'2019 上的阿里团队基于天猫平台、用于召回阶段的一个模型，旨在用多个向量表示用户的多种兴趣，以缓解 / 解决过去（如双塔模型）只用一个单向量模型难以表征用户广泛而相去甚远的多种兴趣。

在天猫的推荐系统中，团队发现用户每天与多种物品发生交互，且交互物品往往不属于同一类别，可能在连续的交互序列中同时包括生活用品、健身器材、数码产品……过去的业内模型多为将用户所有信息拼接后经过网络变换，或是 Pooling 聚合的方式来融合用户的多种兴趣成为 一个向量 ，这可能导致将用户兴趣表征为一个奇怪的区域。

而召回阶段的目的正是检索用户可能感兴趣的物品，精确全面的用户兴趣表征有利于提高召回质量。

胶囊神经元和动态路由 ¶

模型的核心是胶囊网络，该网络采用了动态路由算法能非常自然的将历史商品聚成多个集合，每个集合的历史行为进一步推断对应特定兴趣的用户表示向量。胶囊网络和动态路由出自计算机视觉领域 Dynamic Routing Between Capsules，可以看浅谈胶囊网络与动态路由算法 省流。

由于提出胶囊网络的论文和 MIND 论文使用的符号不完全一致（或者说几乎完全不一致……），所以下面谨用“原论文”表示提出胶囊网络的论文，否则默认为 MIND 论文。

胶囊神经元 (Capsule neuron) ¶

如下左图所示是一个传统的神经元，其输入是多个标量，输出是一个标量，所以论文中认为这是一种 \(\text{scalar} \rightarrow \text{scalar}\) 模式。

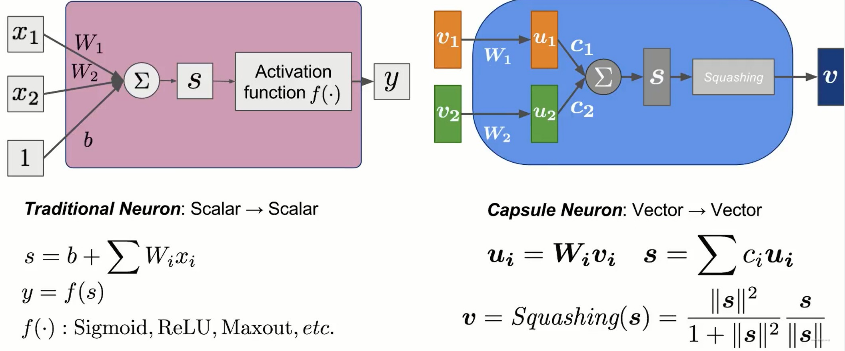
而胶囊网络期望构建一种 \(\text{vector} \rightarrow \text{vector}\) 模式，总体架构类似，具体如上右图。可以发现主要区别在于：

• 输入的向量在进行加权前进行了一次线性变换
• 将激活函数替换为 \(\mathrm{Squashing}\) 操作
  • 左半部分依据输入的 \(L_{2}-\text{norm}\) 进行压缩
  • 右半部分进行向量归一化
• 需要注意的是，这里的 \(W_{i}\) 是通过方向传播更新计算的；但是 \(c_{i}\) 是依据动态路由机制计算，原论文称其为耦合系数 (coupling coefficients) 。

动态路由 (Dynamic routing) ¶

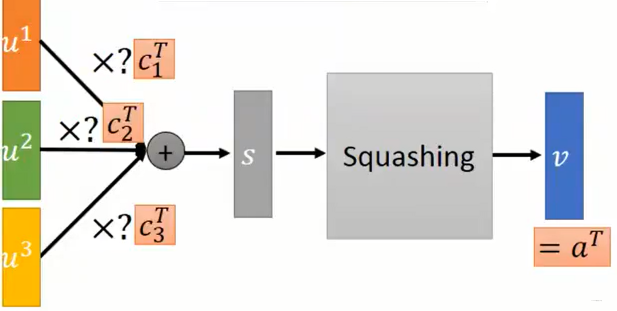
在动态路由机制中，\(c_{i}\) 是通过迭代得到的权重分布，满足 \(\sum_{i} c_{i} = 1\)；在原始论文中使用 softmax 对 logits \(b_{i}\) 进行激活得到，故而实际上对 \(b_{i}\) （原论文称其为路由逻辑值 (routing logit)）进行更新迭代：

直观上理解，在每一轮迭代得到 \(a^{r}\) 后，\(b_{i}\) 的提升程度为 \(a^{r}\cdot u^{i}\) 即输出与输入的相似度；也就是说输出会朝着与它更加相近的输入靠近，而逐渐远离不相干的输入，实现了一个“动态选择”聚类，将那些暂时不相干的输入踢了出去。

类似于 RNN 的迭代，整个胶囊网络的计算如下所示：

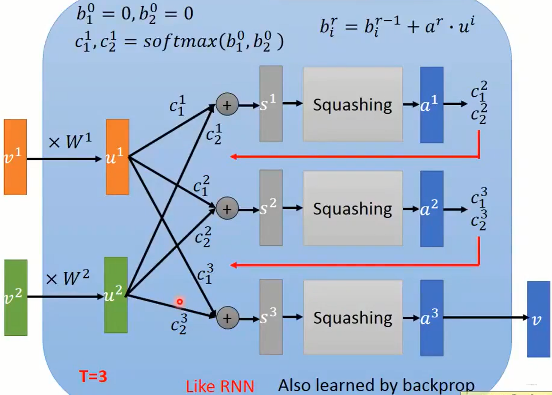
MIND 架构概览 ¶

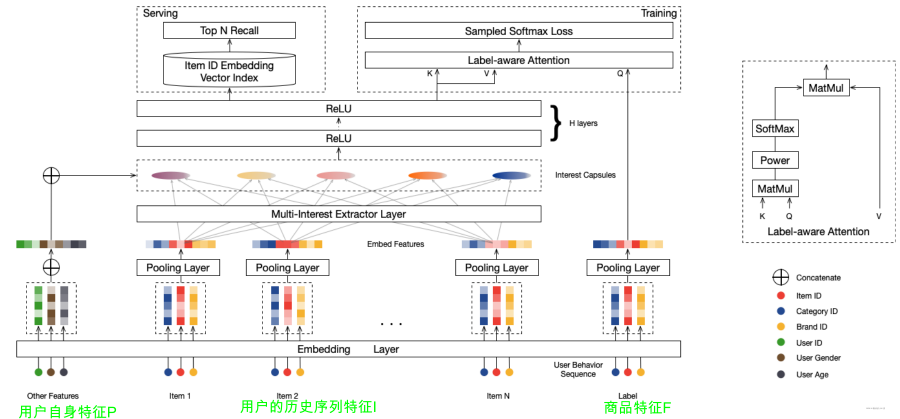
MIND 网络架构如上图所示：

1. 输入：由三部分组成，用户特征 P、物品特征 F、用户行为历史序列特征 I
2. Embedding Layer：将特征嵌入为向量
3. Pooling Layer：对每组特征向量进行池化操作 各得到一个向量
4. 特征 I 经过一个 Multi-Interest Extractor Layer 提取多个兴趣胶囊
5. 特征 P 与兴趣胶囊拼接输入 DNN

嵌入层和池化层 (Embedding & Pooling Layer) ¶

召回任务的目标是对于每一个用户 \(u \in \mathcal{U}\)，能够从所有物品池 \(\mathcal{I}\) 中检索与用户兴趣相关的数千个物品。在上面的架构图中，我们样本为一个三元组 \((\mathcal{I}_{u}, \mathcal{P}_{u}, \mathcal{F}_{i})\)：

• \(\mathcal{F}_{i}\): 物品 i 的自身特征
  • 通常包括分类 id 特征 （如店铺 / 品牌 id）有利于冷启动
  • 采用平均池化，得到 \(\vec{e}_{i}\)
• \(\mathcal{I}_{u}\): 用户 u 交互过的物品集合
  • 获得所有交互过物品的表示集合 \(E_{u} = \{\vec{e}_{j}\}_{j \in \mathcal{I}_{u}}\)
  • 有时也会额外包括分类 id 特征
• \(\mathcal{P}_{u}\): 用户 u 的自身特征
  • 通常包括年龄、性别等
  • 采用向量拼接，得到 \(\vec{P}_{u}\)

MIND 的 核心任务在于学习一个从特征到向量 / 矩阵的用户表示映射 ：

其中 k 表示的是捕捉的用户兴趣数量，d 是一个兴趣的嵌入维度。物品的表示映射表示为：\(\vec{e}_{i} = f_{item}(\mathcal{F}_{i}) \in \mathbb{R}^{d \times 1}\)

而在最后评估用户与物品的相似情况时，采用的是最大化池：

多兴趣提取层 (Multi-Interest Extractor Layer) ¶

动态路由再探 ¶

即前文所提到的胶囊网络，只是论文中的表达有些不同（后面有几乎等价的映射表格，莫急）。我们假设胶囊网络有两层，即：

• 低阶胶囊 \(\vec{c}_i^l\in\mathbb{R}^{N_l\times1},i\in\{1,\ldots,m\}\)
  • \(N_{l}, m\) 分别为胶囊维度和个数
• 高阶胶囊 \(\vec{c}_j^h\in\mathbb{R}^{N_h\times1},j\in\{1,\ldots,n\}\)
  • \(N_{h}, n\) 分别为胶囊维度和个数

连接低阶胶囊 i 和高阶胶囊 j 的权重 / 耦合系数 (oupling coefficients) 使用 \(w_{ij}\) 表示，且同样由 softmax 计算：

所以我们同样是迭代更新路由逻辑值 \(b_{ij}\)，但是更新逻辑有些不同，使用

其中 \(S_{ij} \in \mathbb{R}^{N_{h} \times N_{l}}\) 是待学习的双线性映射矩阵（相当于原论文中的 \(W_{i}\)，转换矩阵），并计算 j 的候选向量：

进行非线性压缩变换得到高阶胶囊的向量表征：

将公式类比不难发现（情况下为了针对从多个低阶到多个高阶而下标有区别）：

行为到兴趣 (Behavior to Interest, B2I) 动态路由 ¶

将行为序列嵌入为行为胶囊，希望学习“行为胶囊（低阶，\(\vec{e}_{i}\)） -> 兴趣胶囊（高阶，\(\vec{u}_{j}\)）” 的映射关系。相比经典的动态路由，B2I 动态路由做出了以下改进：

1. 共享双向映射矩阵 S
   • 用户行为序列长度可变，共享 S 更具普遍性
   • 我们希望兴趣胶囊映射在同一向量空间中，计算路由逻辑值 \(b_{ij} = \vec{u}_{j}^{T}S \vec{e}_{i}\)
2. 随机初始化 \(b_{ij}\) 而非初始化为 0
   • 因为共享了 S，改为通过高斯分布随机采样
3. 动态调整兴趣数量
   • 在前面我们提到兴趣本身是一个“聚类”思想，用户行为序列不同对应的聚类中心数量不同，也即兴趣数量不同，从 K 个自适应调整到 \(K_{u}'\) 个
   • \(K_u^{\prime}=\max\left(1,\min\left(K,\log_2\left(|\mathcal{I}_u|\right)\right)\right)\)

最后算法流程如下，如果还看不懂可能要再回顾一下前面的内容了。

训练和服务 ¶

训练 ¶

训练时使用到标签感知注意层 (Label-aware Attention Layer)，结合名称以及从框架图中我们可以看到标签感知注意层的输入为 K,V,Q ，且：

• 物品标签 \(\vec{e}_{i}\) 作为查询 Q
• 用户 u 多兴趣向量组合（矩阵）\(V_{u}\in \mathbb{R}^{k \times d}\)，既是键 K 也是值 V
  • k 为兴趣数量，d 为向量维度
• 超参数 p 用来调整注意力的分布
  • 结合下面的公式可以发现 p 越小不同兴趣的间的注意力差距越小
  • p = 0 时所有兴趣的注意力相同

显然（和 DIN 类似）基于缩放点积注意力机制 (\(\mathrm{Attention}(Q, K, V) = V \mathrm{softmax(QK^{T} / \sqrt{ d })}\)，这里做了些小修改 ) 有：

然后就是经典的计算概率，极大似然 / 极小负对数似然（论文中没有取负，但也只是说是目标函数，也许默认就是求解收敛最大值吧），sampled softmax 学习到映射 \(f_{user}\)

$$ \Pr(i|u)=\Pr\left(\overrightarrow{e}i|\overrightarrow{v}_u\right)=\frac{\exp\left(\overrightarrow{v}_u^\mathrm{T}\overrightarrow{e}_i\right)}{\sum \Rightarrow}\exp\left(\overrightarrow{v}_u^\mathrm{T}\overrightarrow{e}_j\right)

L=\sum_{(u,i)\in D}\log\Pr(i|u) $$

服务 ¶

在线服务时不需要标签感知注意层，直接使用 \(f_{user}\) 得到用户多兴趣向量，在物品池中使用 ANN 检索 topN 物品召回。

Sequential Deep Matching model (SDM)¶

我们知道了学习用户历史行为序列很重要， 那么假设序列很长呢？这时候直接用模型学习长序列之间的演进可能不是很好，因为很长的序列里面可能用户的兴趣发生过很大的转变，很多商品压根就没有啥关系，这样硬学，反而会导致越学越乱，就别提这个演进了。

SDM 模型也是 CIKM'2019 上阿里团队的一篇 paper 中提出的，团队认为用户在短期的兴趣是比较集中的，交互的商品较为类似，比直接学习整个长序列更加靠谱。SDM 将用户行为序列根据交互时间分为短期和长期会话 (session)，并分别采取相应的措施去学习用户的短期兴趣和长期偏好，并设计了一个门控网络有选择地融合长短期兴趣，得到用户最终的兴趣向量。

架构概览 ¶

会话 (session) 划分：

• 相同会话 id 的商品 \(i \in \mathcal{I}\)
• 交互时间间隔小于 \(t_{0}\) 的商品
• 一个会话中商品数量不超过 \(m_{0}\) 个，多余部分放入下一个会话

会话定义：

• 最近一次会话为用户 \(u \in \mathcal{U}\) 的短期行为 \(\mathcal{S}^{u} = [i_{1}^{u}, \dots, i_{t}^{u}, \dots, i_{m}^{u}]\) ，编码在 \(s_{t}^{u}\) 中
• 长期对话用过去 \(T_{0}\) 时间内的 其余会话组成，使用 \(\mathcal{L}^{u}\) 表示，编码在 \(p^{u}\) 中

经过门控神经网络得到用户行为预测向量 \(o_{t}^{u} \in \mathbb{R}^{d \times 1}\)，剩下的部分就经典的训练和召回了。

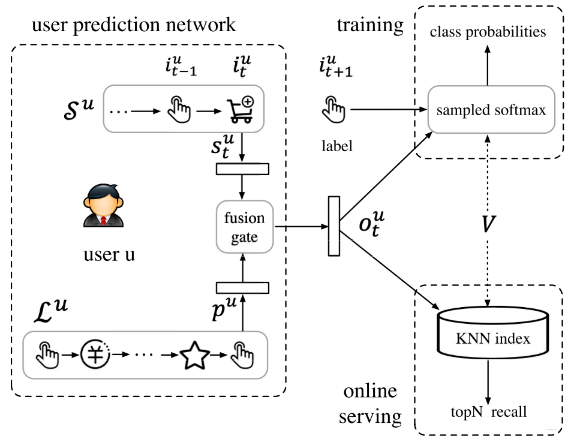
在 SDM 中的物品嵌入时应用到了辅助信息 (Side Information) \(\mathcal{F}\)，具体而言使用了 leat category, fist level category, brand,shop，包括物品本身共 5 项，分别嵌入（\(\boldsymbol{e}_i^f=\boldsymbol{W}^f\boldsymbol{x}_i^f\in\mathbb{R}^{d_f\times1}\)）后进行拼接，有：

用户画像 \(\mathcal{P}\) 部分是类似地，特征分别嵌入（\(e_{u}^{p}\)）后拼接：

现在就剩下 \(\mathcal{L}^{u} \rightarrow p^{u}, \mathcal{S}^{u}\rightarrow s_{t}^{u}, (p^{u}, s_{t}^{u})\rightarrow o_{t}^{u}\) 这三部分需要拆解，论文中一张图展示的较为清晰了：

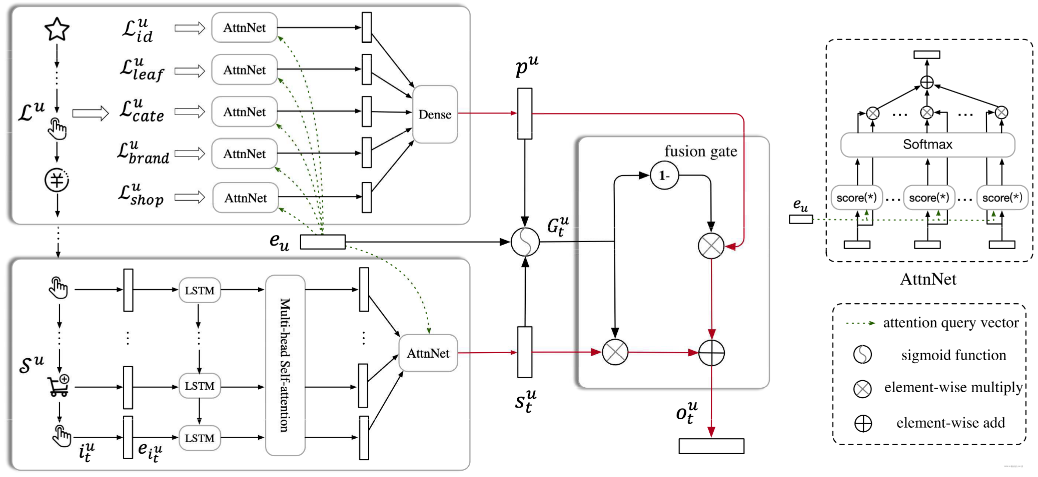
短期会话：循环层 ¶

为了捕捉并表征短期序列数据中的全局时间依赖性，采用长短期记忆（LSTM）网络作为循环单元。

暂时没看 LSTM 和多头注意力，先放着。

长期会话：注意力机制 ¶

长期行为往往来自不同的特征：

对每个 \(f_{k}^{u} \in \mathcal{L}_{f}^{u}\) 通过 \(W^{f}\) 变换（其实就是从稀疏的独热码变为稠密嵌入向量）得到 \(g_{k}^{u} = W^{f}f_{k}^{u} \in \mathbb{R}^{d\times 1}\) 。基于点积注意力机制得到

拼接（\(z^{u} = \mathrm{concat}(\{z_{f}^{u}\mid f \in \mathcal{F}\})\)）后输入一个全连接层：

门控网络：行为融合 ¶

训练一个门控向量决定在时间 t 时短期和长期的贡献分配（其中 \(\odot\) 表示哈达玛乘积，即逐元素相乘得到新的等维向量）：

对于可能冲突的两个向量融合，我们不一定非得加权或拼接了，还可以通过门控机制让网络自己去学。

如果这对你有用的话，请给我点个star吧 ===>