Vector-based¶
Deep retrieval¶
简要来说,在前面的学习中,我们使用过向量作为物品和用户中间的关联中介,下面将要介绍使用路径作为物品和用户的中介。
物品 - 路径索引 ¶
deep retrieval 将物品表征为路径,在训练阶段一个物品可以表示为多条路径;在召回时一条路径可以指向多个物品。我们期望建立 Path -> List<Item> 的索引,基于用户本身特征寻找路径,最后映射到对应的物品进行召回。
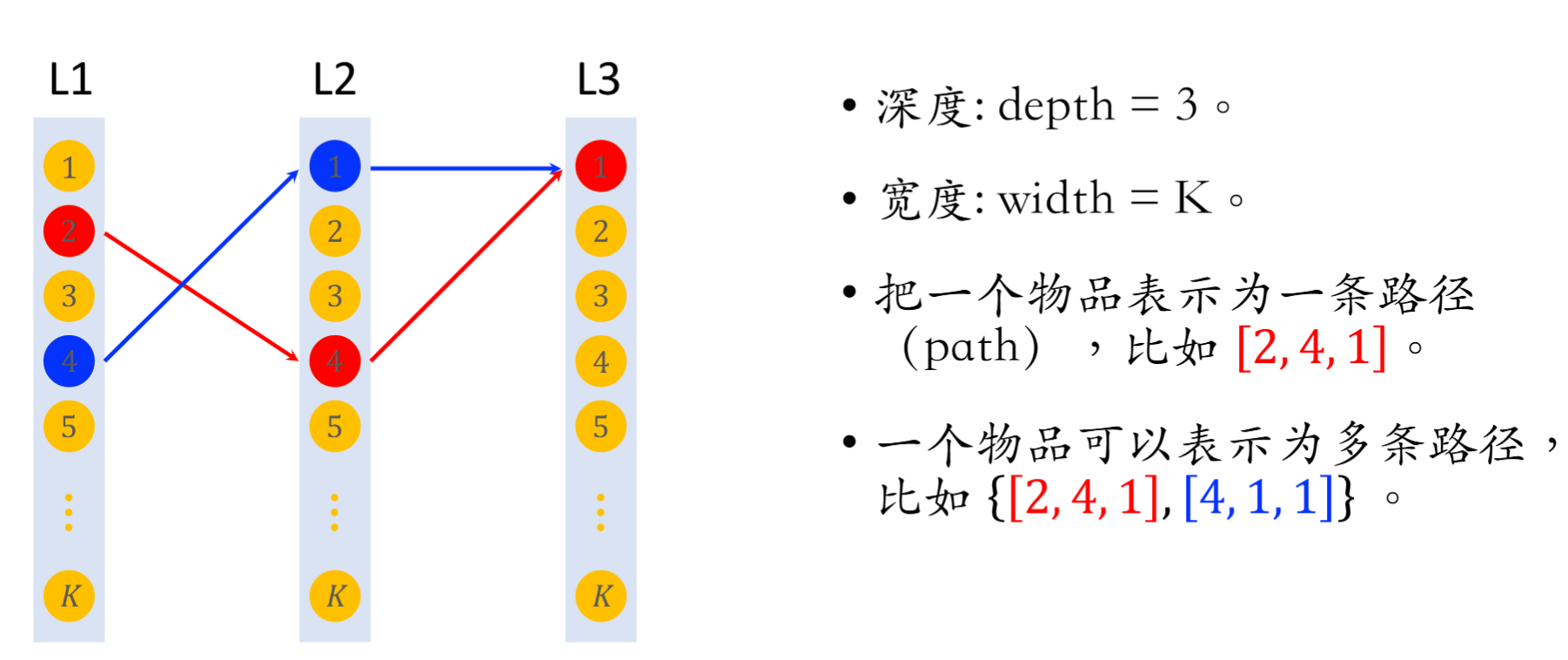
预估模型 ¶
在已知用户特征 x 的情况下,我们希望为用户召回一些物品,可以看成是希望找到对应的路径,召回路径对应的物品即可。类似于序列模型的生成,我们逐步去计算前往每一个节点的概率(例如上图中三层
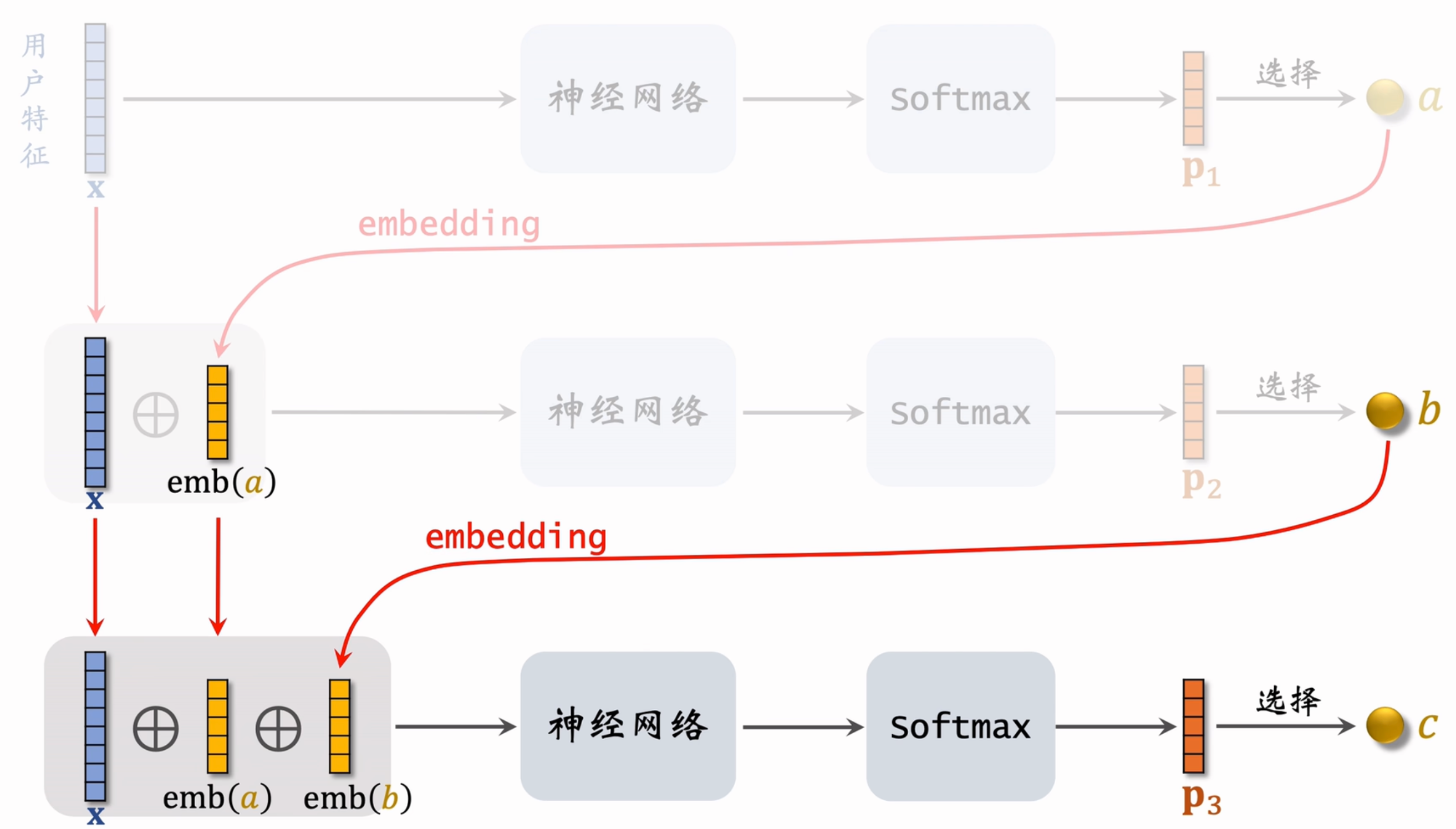
- \(p_{1} = p(l_{1}|x), p_{2} = p(l_{2} | x, l_{1}), p_{3} = p(l_{3}|x, l_{1}, l_{2})\)
- \(P = p_{1} \cdot p_{2} \cdot p_{3}\)
这样我们找到了预估模型对于用户 x 应该在路径 \([l_{1}, l_{2}, l_{3}]\) 的概率 P,用于学习评估。对于 \(p_{1}, p_{2},p_{3}\) 这样的“概率”,神经网络很擅长做这些,也即可以认为通过神经网络,基于已有前缀路径的条件下去为当前层每个节点计算条件概率,取概率最 / 较高者。
线上召回 ¶
有了上面的准备,我们可以基于用户特征找到一条或多条路径,召回路径背后对应的物品。
假设每层节点数为 k,哪怕只有三层的模型路径数也达到了 \(k^{3}\),计算量相当恐怖。基于此处为逐层搜索路径,我们很容易想到 beam search。当 BEAM_SIZE=1 时,即每一步都“贪心地 ”选择概率最高的那条路径。当 BEAM_SIZE=k >1 时,也即我们在每一层都保留 k 条路径,在下一层扩展后计算对应的分数并保留 top-k 路径
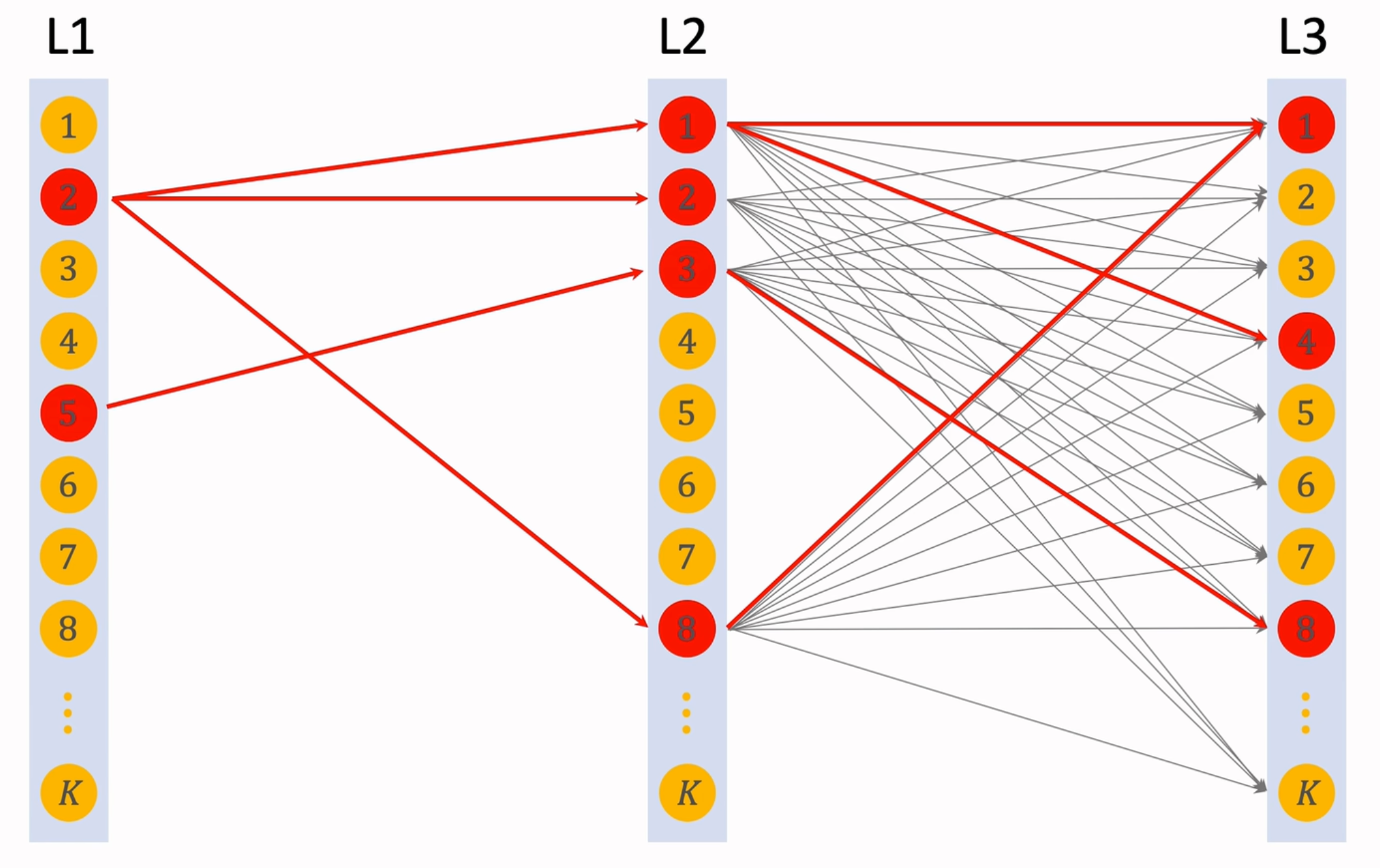
对于召回的物品数量如果超过了限制,利用简单的排序模型筛选掉一部分即可。
模型训练 ¶
损失函数 ¶
训练时需要同时学习神经网络参数和物品表征(神经网络用于评估、选取物品;物品表征即物品与路径之间的映射关系,路径可以对应多个物品,物品也可以对应多条路径
可以认为,如果用户表现出对物品 i 的兴趣,就提高其对应路径 \(path_{j}\) 的关联程度。
物品表征 ¶
上面的神经网络本质学习的是用户与路径的关系 \(score(\text{user,path})=p(\text{path}|\text{user})\);物品与路径的关系也依托与此,记为 \(score(\text{item, path}) = \sum_{user}p(\text{path|user}) \times click(\text{item, user})\),依据 score 选取 top-k 作为物品 item 的表征。
路径更新 ¶
为了避免过多的物品聚集在一条路径上,我们引入正则项;在论文中使用了路径上物品数量的 4 次方作为正则罚项 reg(path)。 假设我们已经将物品表征为 J 条路径 \(\{path_{j}\}, j \in [J]\),随机选择 \(l \in [J]\),对于 \(\{path_{j}\}_{j\neq l}\) 保持不变,更新 \(path_{l}\):
其中 \(\text{loss}(\text{item}, \Pi)\) 表征了物品与这一批路径的相关性,后者则是对这条路径上物品数量的罚项,避免过多物品聚集在一起。
Word2vec/Item2vec¶
“You shall know a word by the company it keeps” (J. R. Firth 1957)
一个单词的含义由其周边单词决定,因此我们关注单词与一定距离(窗口)内单词的关系。
经过 wordnet(维护成本高、难以捕捉特定情况下的含义
Word2vec 包含两个模型,Skip-gram 与 CBOW。
Skip-gram(SG)¶
考虑一串富含语义的文本,对于某一个中心单词 (center),及其周边词 (outsides),我们希望他们以当前顺序排列这一事实最大化,基于条件概率和极大似然估计有:
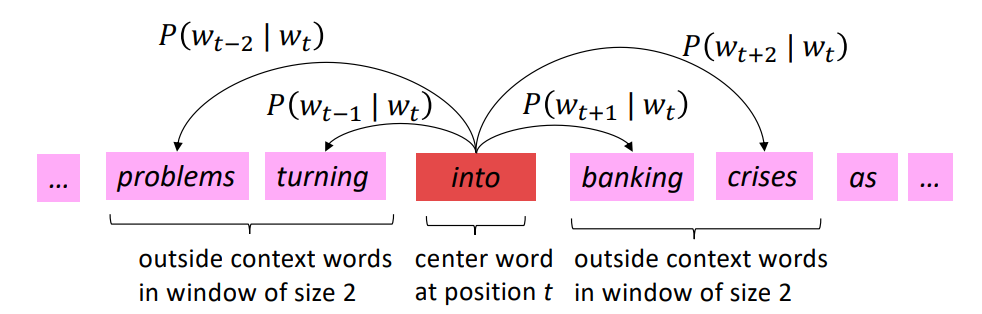
取其负对数似然,考虑模型参数并针对时间步缩放有:
上式即为skip-gram 的损失函数,通过最小化损失函数找到合适的 \(\theta\),其中可以获取词向量,如下图所示
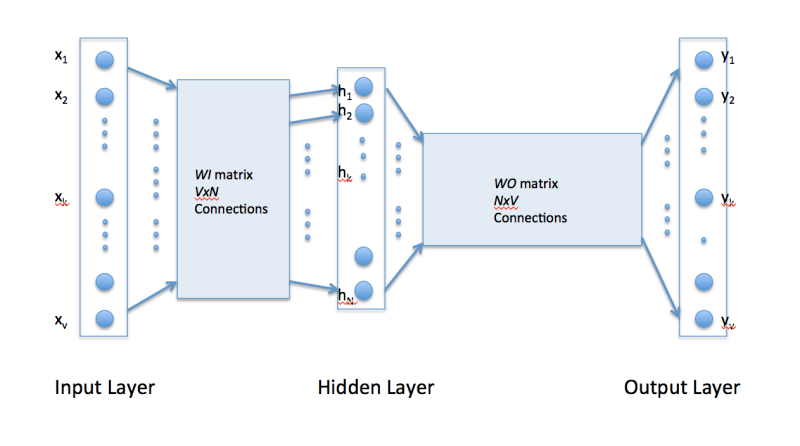
- Input Layer: 输入为 1xV 的 one-hot code ,其中 V 为单词表长度,故而代表了某一个单词;这里我们输入中心词对应的 one-hot code
- \(W_I\): VxN 的参数矩阵,其中 N 表示期望单词嵌入的向量空间维度;\(W_{I}\) 的每一行对应一个单词作为中心词的词向量 \(v_{c}\)
- Hidden Layer: 取出的中心词的词向量 \(v_{c} \in \mathbb{R}^{1 \times N}\)
- \(W_{O}\): NxV 的参数矩阵,N 的含义不变;\(W_{O}\) 的每一列对应一个单词作为周边词的词向量 \(u_{o}\)
- Output Layer: 根据矩阵运算可知输出层的每一项目对应于 \(v_{c}u_{o}\) 即中心词与周边词的内积,我们期望其能够表征词之间的相似度;为了转变为概率,还需要对结果进行 softmax:\(P(o|c)=\frac{\exp(u_o^Tv_c)}{\sum_{w\in V}\exp(u_w^Tv_c)}\)
使用 softmax 又不可避免地来到负采样,再抄一遍:
层序 Softmax (Hierarchical Softmax)
在信息论中,哈夫曼编码依托于哈夫曼树构造,越频繁出现的节点距离根节点的距离越近;对于每个节点的出边(自上而下的边
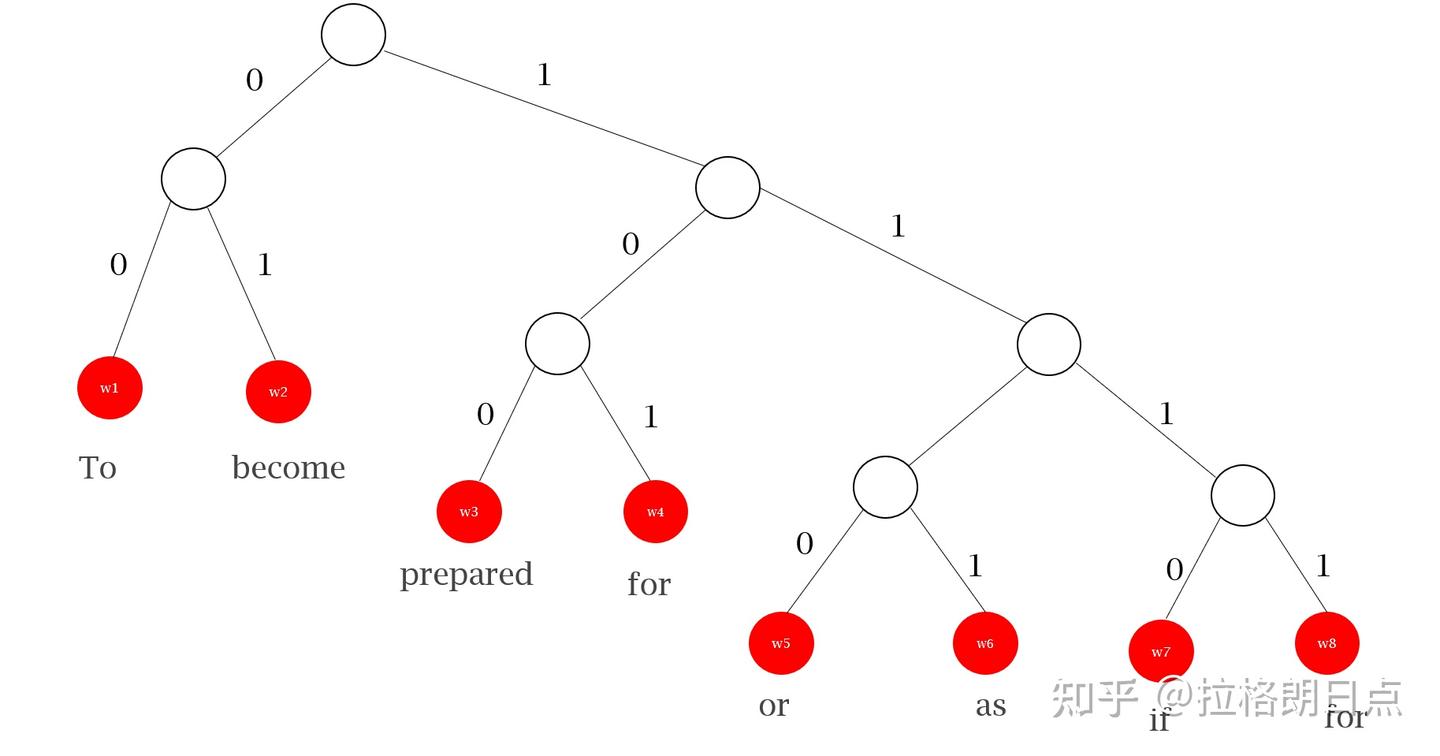
我们知道 Softmax 一般用于多分类问题(word2vec 的 next word prediction 即为一个多分类问题
) ,而基于哈夫曼树(或者说满足特定分布的决策树)我们将其转变为多个二分类问题,代替了 word2vec 模型的 OutputMatrix 部分。层序 Softmax 能够将计算量由 \(O(|V|) \rightarrow O(\log |V|)\),其中 V 为词表。
CBOW¶
依据前文描述可以发现,skip-gram 期望通过中心词预测周边词;而 CBOW 期望能够通过周边词预测中心词(模型结构不变,各层的维度对应进行修改即可)
Item2vec¶
Item2Vec 的原理同样十分简单,它是基于 Skip-Gram 模型的物品向量训练方法;在提出 Item2vec 的论文中,物品相连的训练基于物品集合,而丢弃了集合内部物品的时间、空间关系;论文中使用 \(u_i, u_{i}+v_{i}, [u_{i}+v_{i}]\) 三种方式表示物品向量。
Airbnb¶
Listing embedding¶
Airbnb 是全球最大的短租平台,包含了数百万种不同的房源 (listing)。类似于语言序列,用户对于房源的点击也是一种序列,这使得基于 Word2vec 学习 listing embedding 变得容易(适用于短期实时
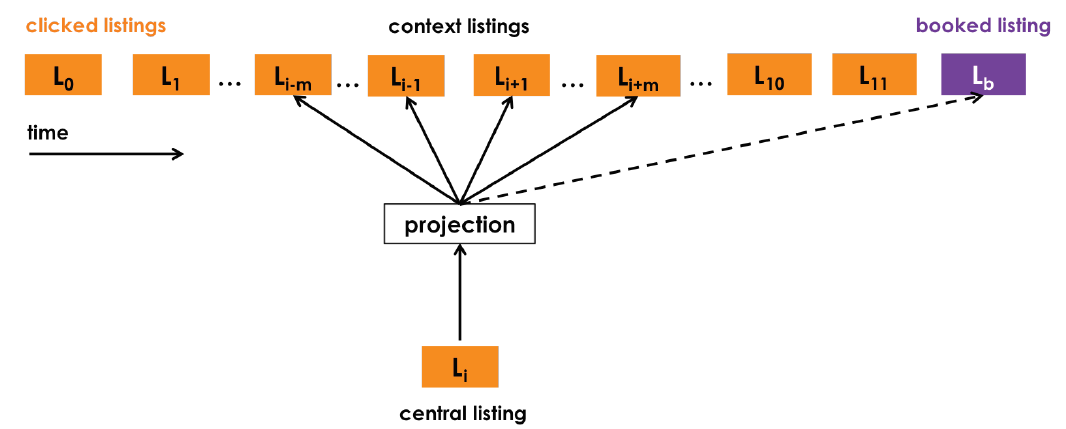
有些不同的是:
最终用户预订的房间应该有其优势,应该被推荐
将 booked listing 作为全局正样本加入优化目标中;
用户预定房间往往在一个地区附近,故连续点击中地区非常靠近,而负样本 \(D_{n}\) 从全部房间源中选择
从 central listing 的同一地区也采样一些负样本;
房源更新比单词快的多,需要面临冷启动问题
要求房主提供地区、价格、类型等信息,在已经 embedding 的 listing 中寻找最相似的若干个,取平均作为新房源的 embedding。
最终优化目标变为:
Type embedding¶
基于点击的 embedding 适用于短期,而在长期中失去了联系(例如用户在一个月前预订了房间而现在又需要预订,且在此期间偏好可能发生了较大改变
不同的是作为同一类物品,房源的属性信息较为同一,易于获取(地理位置、面积、床数量、价格
之后仍然是利用 skip-gram 模型,对 Listing-type / User-type 分别设定目标函数优化
- Listing-type 训练使用 listing 作为“中心词”,user 作为“周边词”
- User-type 训练使用 user 作为“中心词”,listing 作为“周边词”
Airbnb 还考虑了房主拒绝用户(用户评级过低、只接受女性等)的情况,将其作为负样本。
Twin Tower¶
在 Skip-gram 模型中,one-hot code 只是编码了对应的用户 / 物品(可以认为只是用户 / 物品 ID
Factorized Machine (FM)¶
在神经网络出现后因子分解机逐渐被替代,但是其思想仍可一看。
面对用户 / 物品特有的属性(如有用户的性别、物品的体积、用户的年龄和物品的年龄概念不同
线性模型 ¶
线性模型将预测视为特征的加权和(n+1 个参数,只有加法
二阶交叉特征 ¶
为了让模型的预测更加准去,引入更多的特征交互的信息提升模型表达能力:
但是此时参数数量达到了 \(O(n^{2})\) ;考虑由 \([u_{ij}]\) 构成的对称矩阵 U(同时联想到 SVM 中核技巧
进一步的,二阶交叉特征计算的时间复杂度为 \(O(kn^{2})\);但是基于其实际在求和一个矩阵的上半部分,有:
这样计算的时间复杂度减少到 \(O(kn)\)。
- 优点:
- 通过向量内积自适应调整交叉权重,同时不再需要强调是非零特征
- 优化后计算效率高,在稀疏场景下能够自动挖掘长尾低频物品,因而召回和排序阶段均适用(细节有所不同)
- 缺点:
- 最多到特征的二阶交叉,再高阶的无能为力
特征分离 ¶
将用户和物品特征拆分开有:
在召回时我们总是对同一个用户的请求进行分析,因而用户内部的特征交互是无影响的(不改变召回时的分数排序
其中
这表明物品和用户的特征交互可以被分别编码到两个独立向量中,展示了“双塔模型”的可行性。
推荐系统中的双塔模型源自 DSSM(Deep Structured Semantic Model)
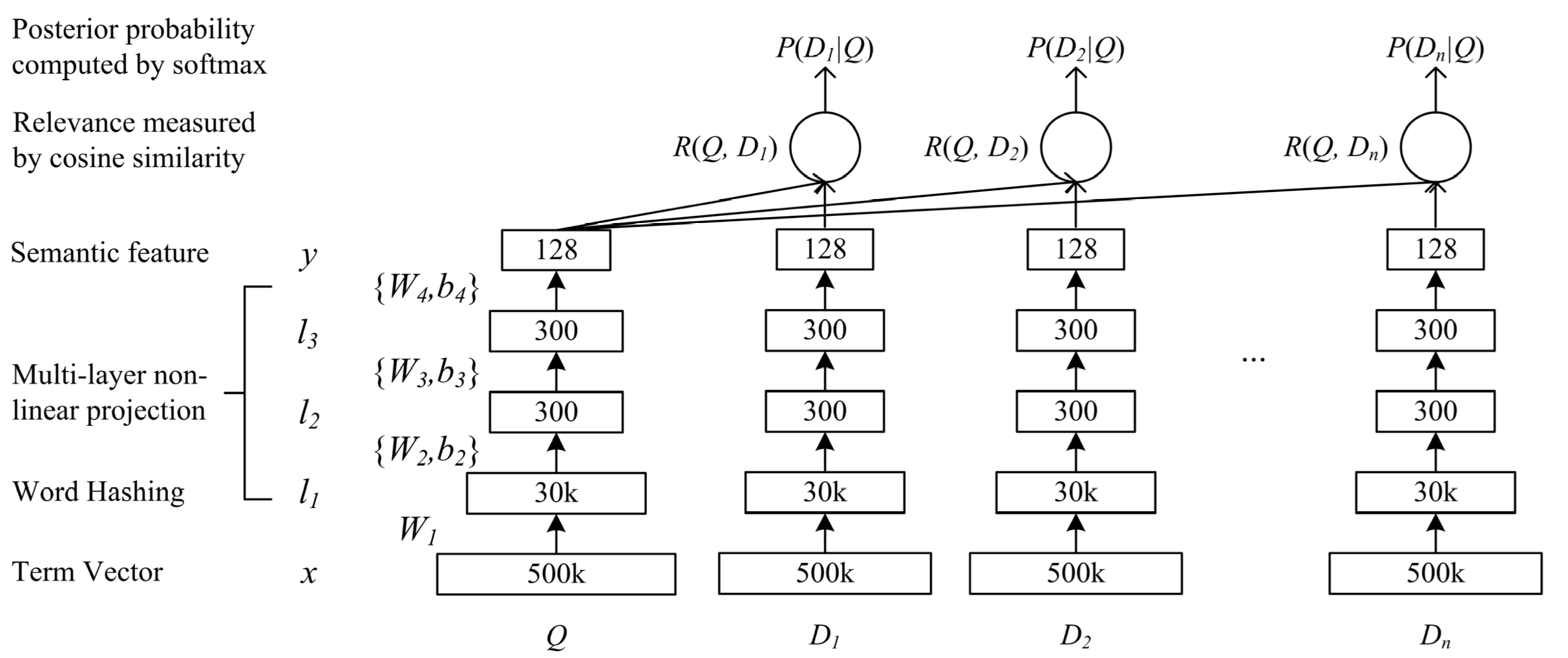
DSSM(Deep Structured Semantic Model) 是由微软研究院于 CIKM 在 2013 年提出的一篇工作,该模型主要用来解决 NLP 领域语义相似度任务,利用深度神经网络将文本表示为低维度的向量,用来提升搜索场景下文档和 query 匹配的问题。DSSM 模型的原理主要是:通过用户搜索行为中 query 和 doc 的日志数据,通过深度学习网络将 query 和 doc 映射到到共同维度的语义空间中,通过最大化 query 和 doc 语义向量之间的余弦相似度,从而训练得到隐含语义模型,即 query 侧特征的 embedding 和 doc 侧特征的 embedding,进而可以获取语句的低维语义向量表达 sentence embedding,可以预测两句话的语义相似度。模型结构如下所示:
经典双塔模型 ¶
由于用户和物品的特有特征不一致,以及 FM 分解暂时可行性,用户和物品可以分别训练形成双塔模型:
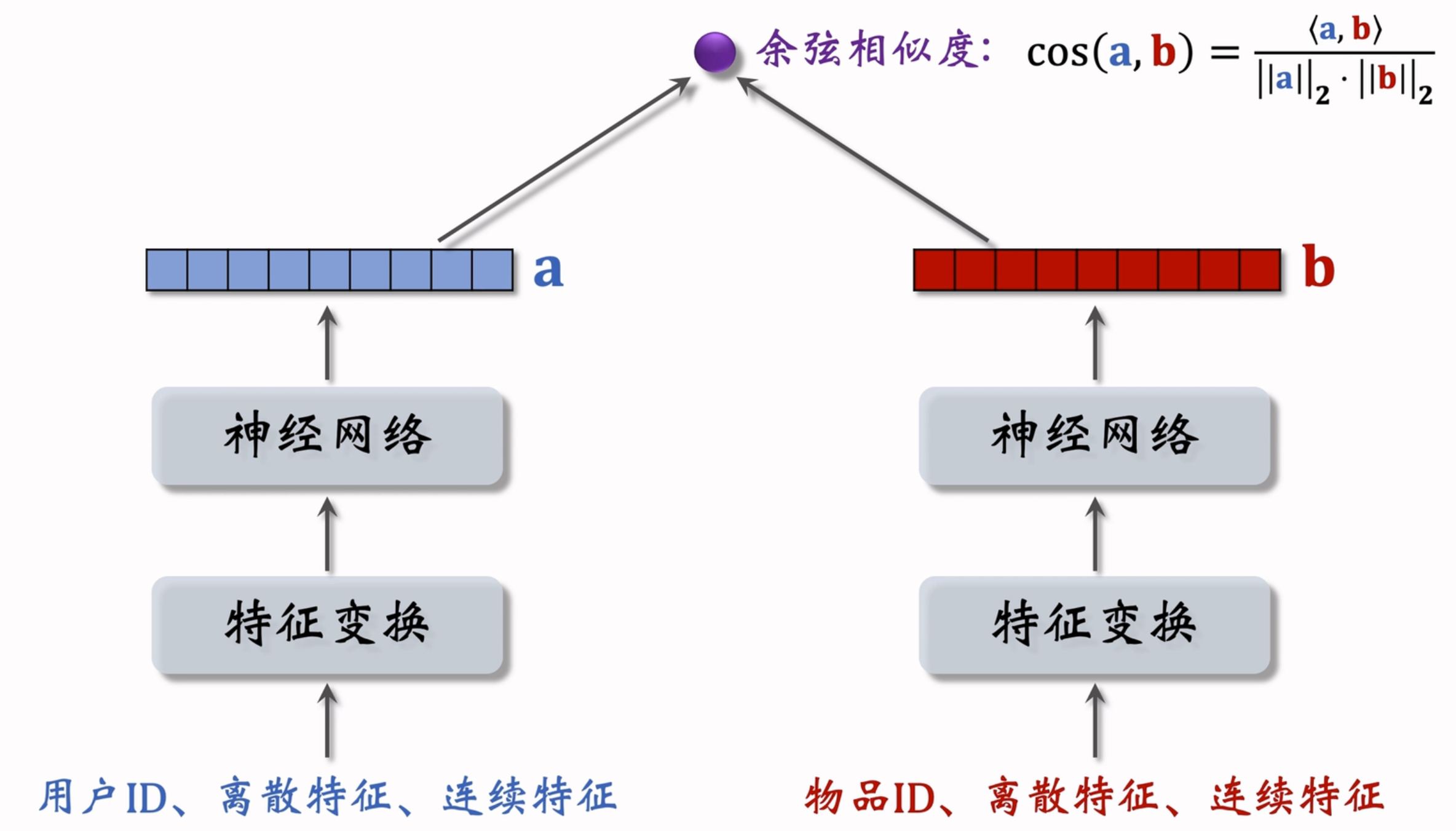
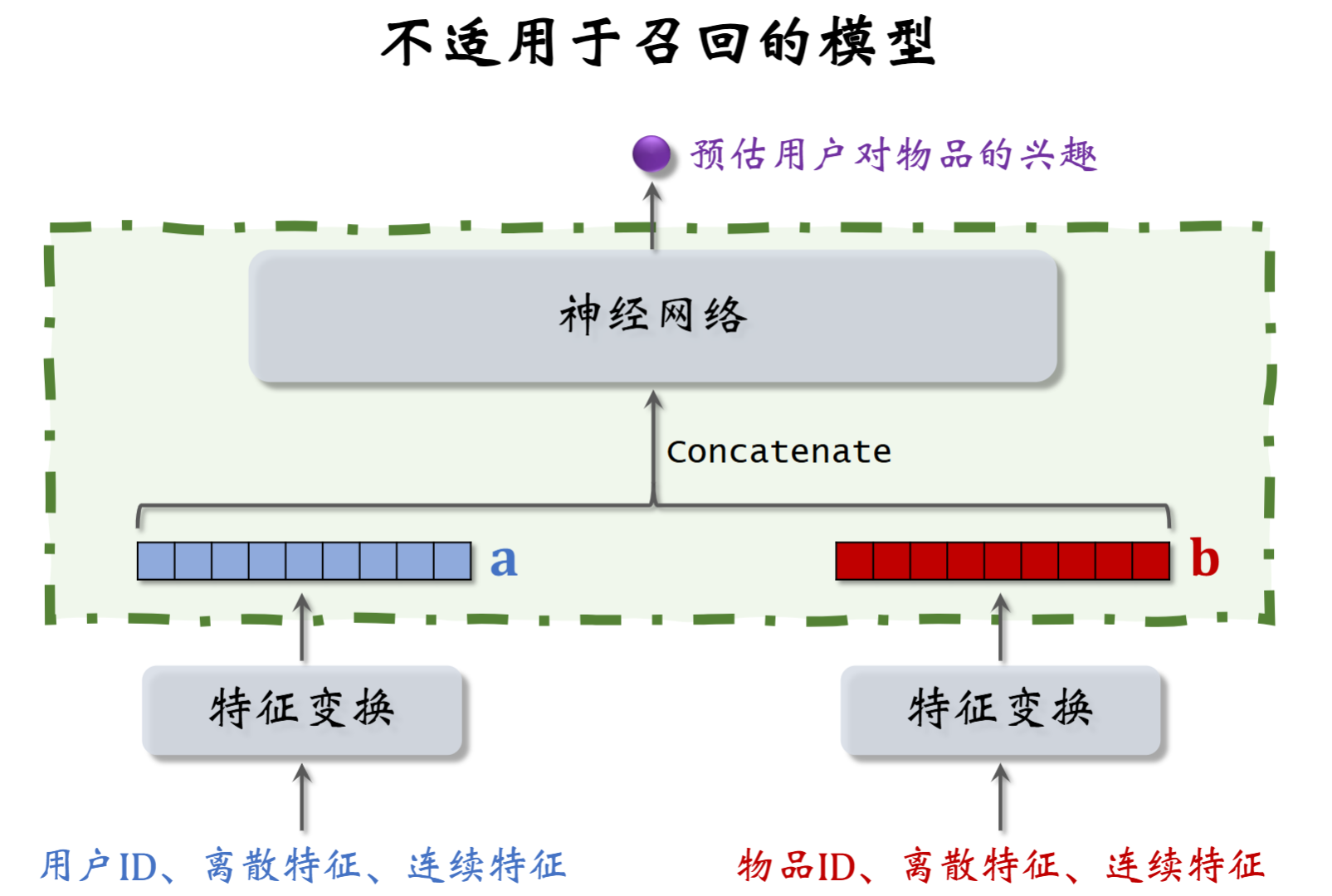
下面的“双塔”模型不适合召回
因为图中用户 / 物品的向量 a/b 在前期就进行了融合,不能够使用最近邻算法找回 top-k;该模型应该用于排序模型等可以计算所有用户与物品相似度的层。
双塔模型变体 ¶
双塔模型在实际推荐系统的召回阶段应用非常广泛,因为其模型结构简单且后期融合的特点在面对海量的数据下能够保持非常快的召回速度。但是模型结构简单也可能导致很多特征信息在早期传递过程中损失。现在也有了一些变体以解决上述问题。
SENet 双塔模型 ¶
SENet 是一种对特征进行交叉筛选的网络,将其添加进入双塔模型中形成 SENet 双塔:
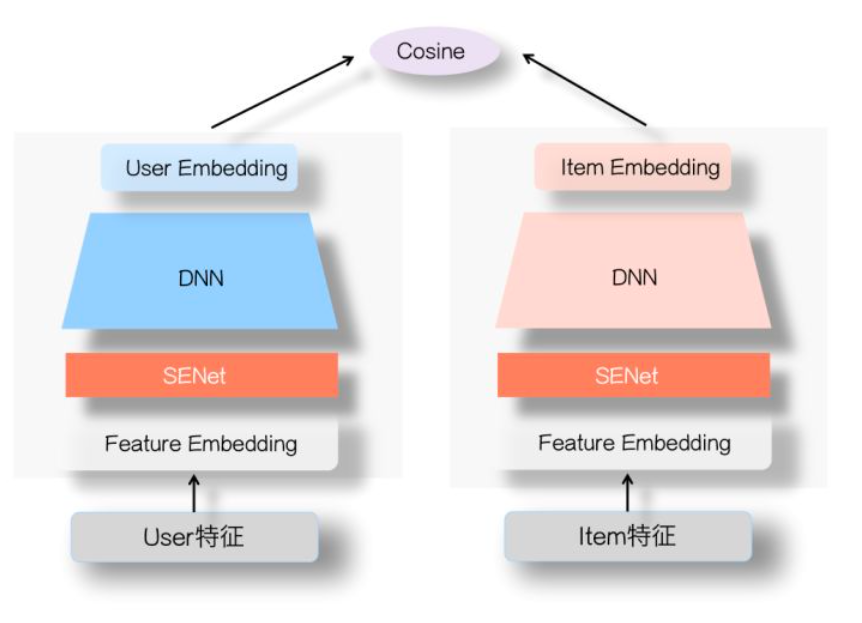
利用 SENet 能够自适应学习特征的重要性,可以一定程度过滤掉长尾且低质的特征,
多目标双塔模型 ¶
针对点击率、点赞率、评论率等多种指标,多目标双塔模型能够共享信息的同时针对不同目标分别优化损失,如下图所示:
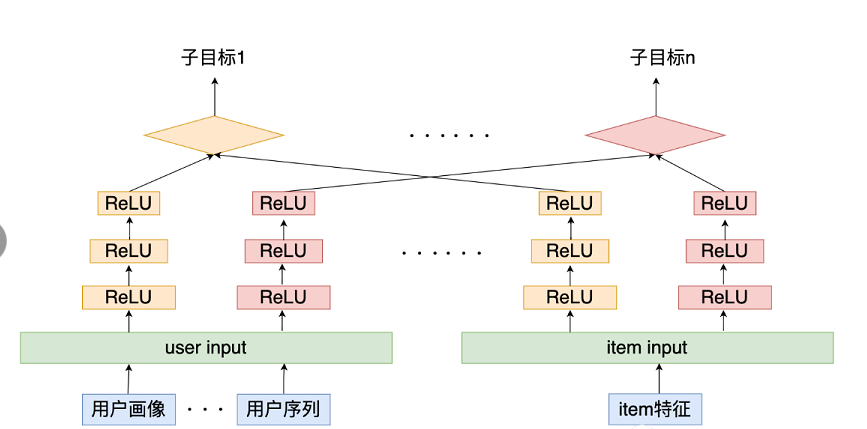
针对不同的目标,用户塔和物品塔分别使用一个 DNN 来捕捉特征,同一个塔的 DNN 共享输入信息。
Youtube 双塔模型 ¶
Youtube 双塔模型的结构上没有较大的新奇之处,样本为三元组 {user, item, reward}:
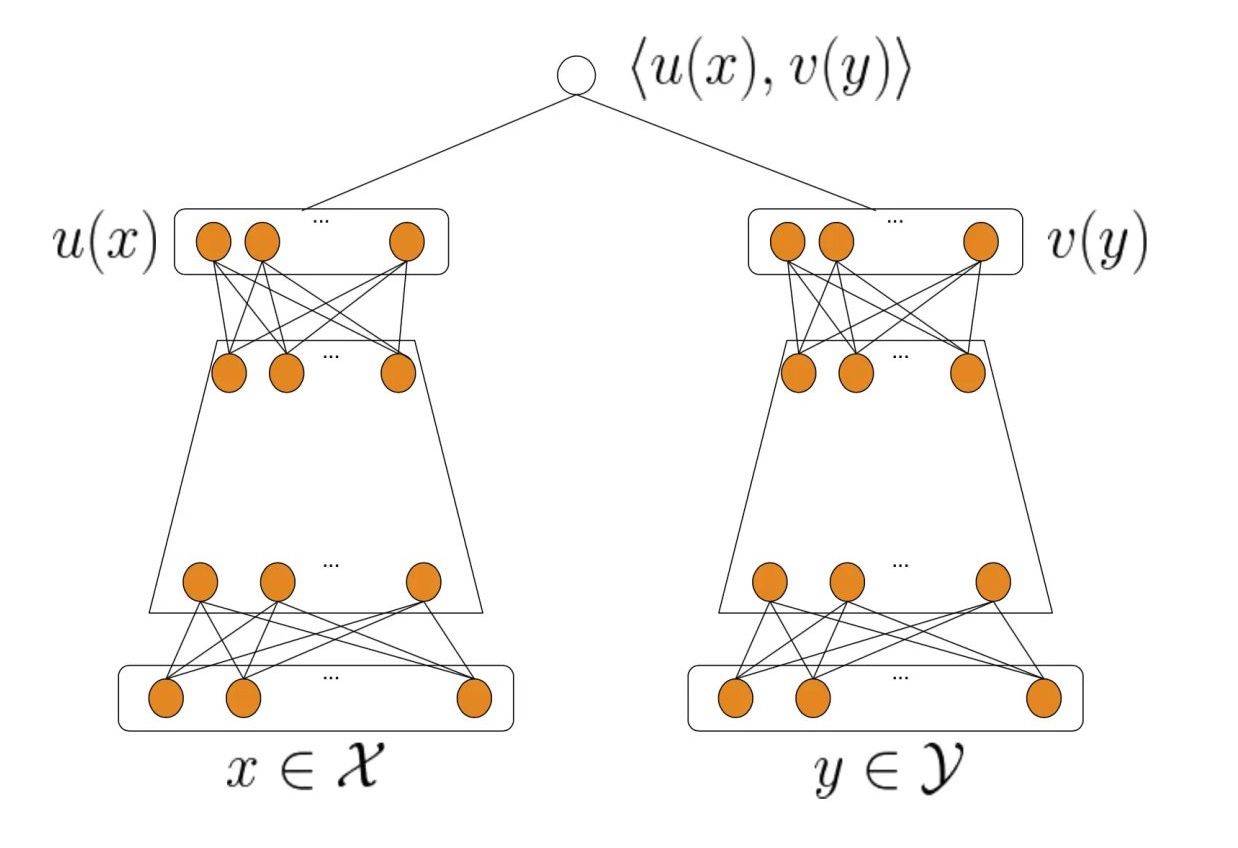
模型输出为 x 与 y 的相似度:\(s(x,y)=\langle u(x,\theta),v(y,\theta)\rangle\)。类似于 YoutubeDNN 对输出进行 Softmax 得到概率分布:\(\mathcal{P}(y\mid x;\theta)=\frac{e^{s(x,y)}}{\sum_{j\in[M]}e^{s(x,y_j)}}\)。考虑奖励 r,加权负对数似然函数为:
同样的,使用负采样来减小开销并进行进行纠偏(\(s^c\left(x_i,y_j\right)=s\left(x_i,y_j\right)-\log\left(p_j\right)\)
在 "3 MODELING FRAMEWORK" 小节的结尾处,提及了两个小 trick (Normalization an Temperature):
- 对 user 和 item 的 embedding 进行归一化(等价于将 s(x,y) 操作由内积改为求余弦相似度
) :
原因在于用户和物品的嵌入向量的欧氏距离可以表示为:
将嵌入向量归一化,这可以得到:
此时内积将转化为欧氏距离,而进行近似最近邻 (Approximate Nearest Neighbor, ANN) 搜索时一般使用的就是欧氏距离,这样的转换保证了训练与检索时的一致性。
- 对内积进行温度调控
论文中提到除以一个超参数是为了让 softmax 的结果更加明显 (sharpen) ,
召回和更新 ¶
- 离线存储:物品向量(数量大、较稳定)
-
线上计算:用户向量(变化频繁)
-
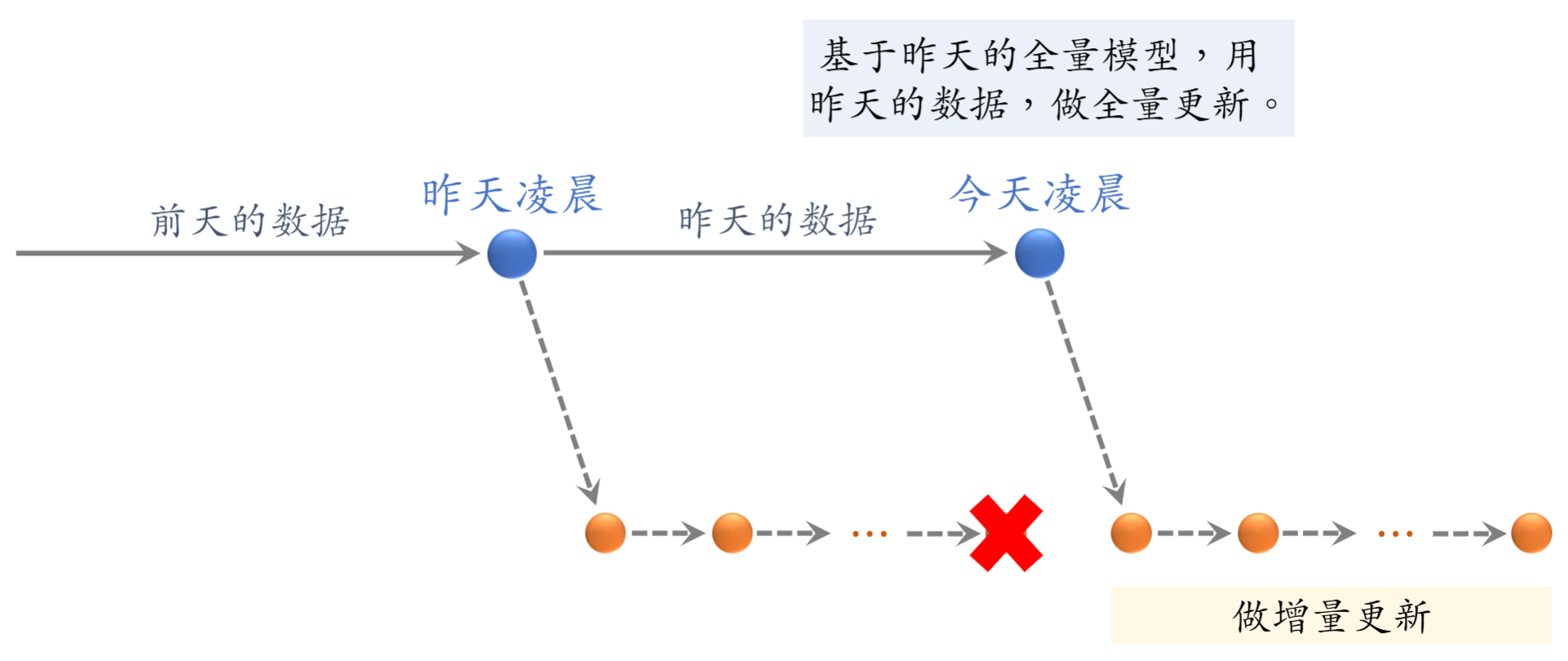
全量更新:利用昨天的数据,在原有参数基础上训练 1 轮,每天数据(TFRecord)只用一遍;发布新的用户塔和物品向量
- 增量更新:每隔一小段时间,实时收集线上数据做流式处理,对模型做 online learning(只更新 embedding layer 参数
, )
在实际工业生产中,增量更新得到的模型只在下一个增量更新模型出现前使用,且在全量更新时使用的是昨天的所有数据(随机打乱比按时间顺序更好
模型训练和样本选取 ¶
- Pointwise : 独立看待正负样本
- 将召回视为简单的二分类模型
- Pairwise: 一对正负样本
- 鼓励 \(cos(a, b^+) > cos(a, b^-)+m\) ,m 为超参数
- Listwise: 一个正样本,多个负样本
- 使用 softmax,交叉熵损失来综合多个负样本
样本选取 ¶
对于正样本,一般选择曝光给用户并点击后的样本即可;对于负样本:
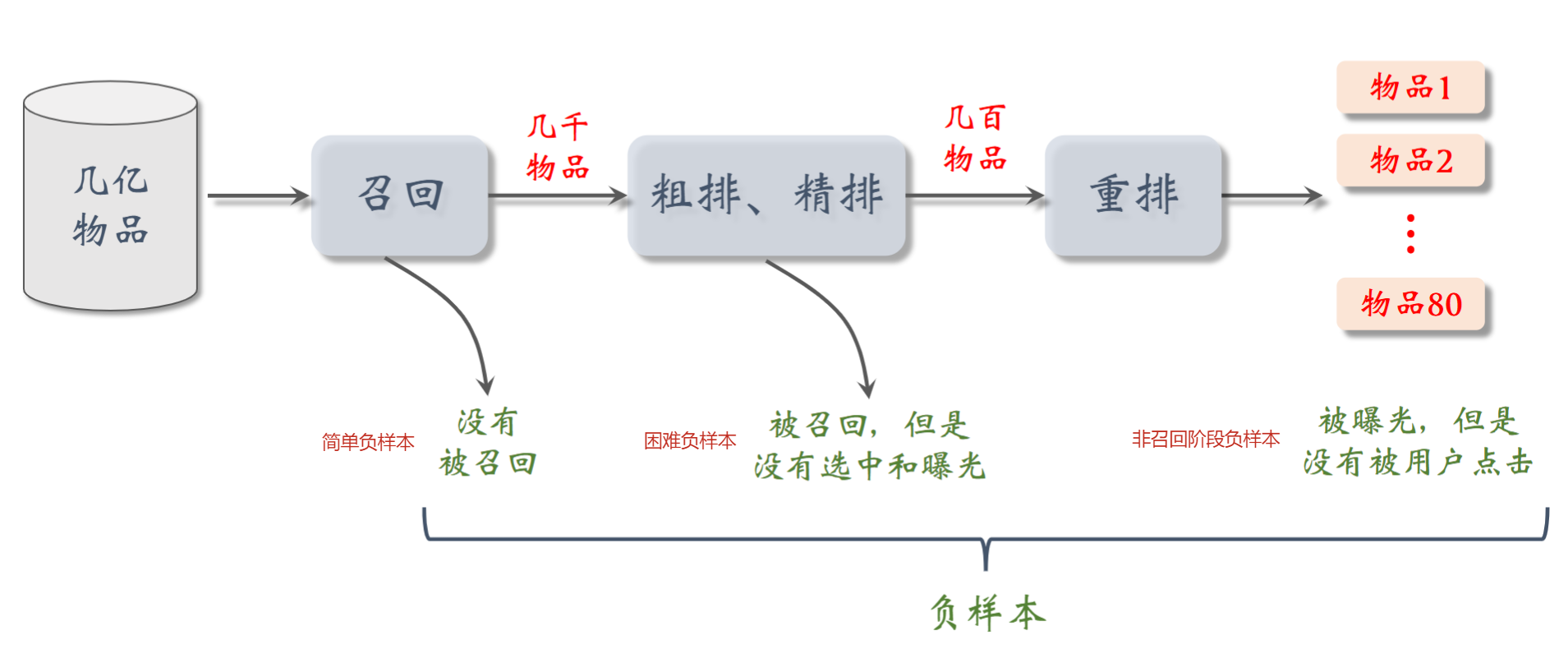
- 未被召回的样本是数据库中的大多数样本,容易被模型区分,故为简单负样本;
- 召回后在排序过程中被筛选的样本已经在一定程度上符合用户兴趣了,较难被模型区分,故为困难负样本;
- 曝光但是未被用户点击,并不能够说明用户不感兴趣,而可能是用户更加偏好点击了的那些而已
- 需要明确每个阶段的目的:召回是排除用户基本不感兴趣的物品,排序是找到用户最感兴趣的物品
- 应该作为排序模型的负样本而非召回模型
Listwise 训练 ¶
依据经验正负样本比例为 1:2 ~ 1:3 较为合适,所有使用 Listwise 的训练模式较多;使用 softmax 后我们期望正样本对应的预估概率接近 1,其他接近 0,结合使用交叉熵损失得到双塔模型整体训练损失为:
由于按照 batch 进行训练,对所有物品取平均:\(\frac1n\sum_{i=1}^nL_\text{main}[i]\)
自监督学习 ¶
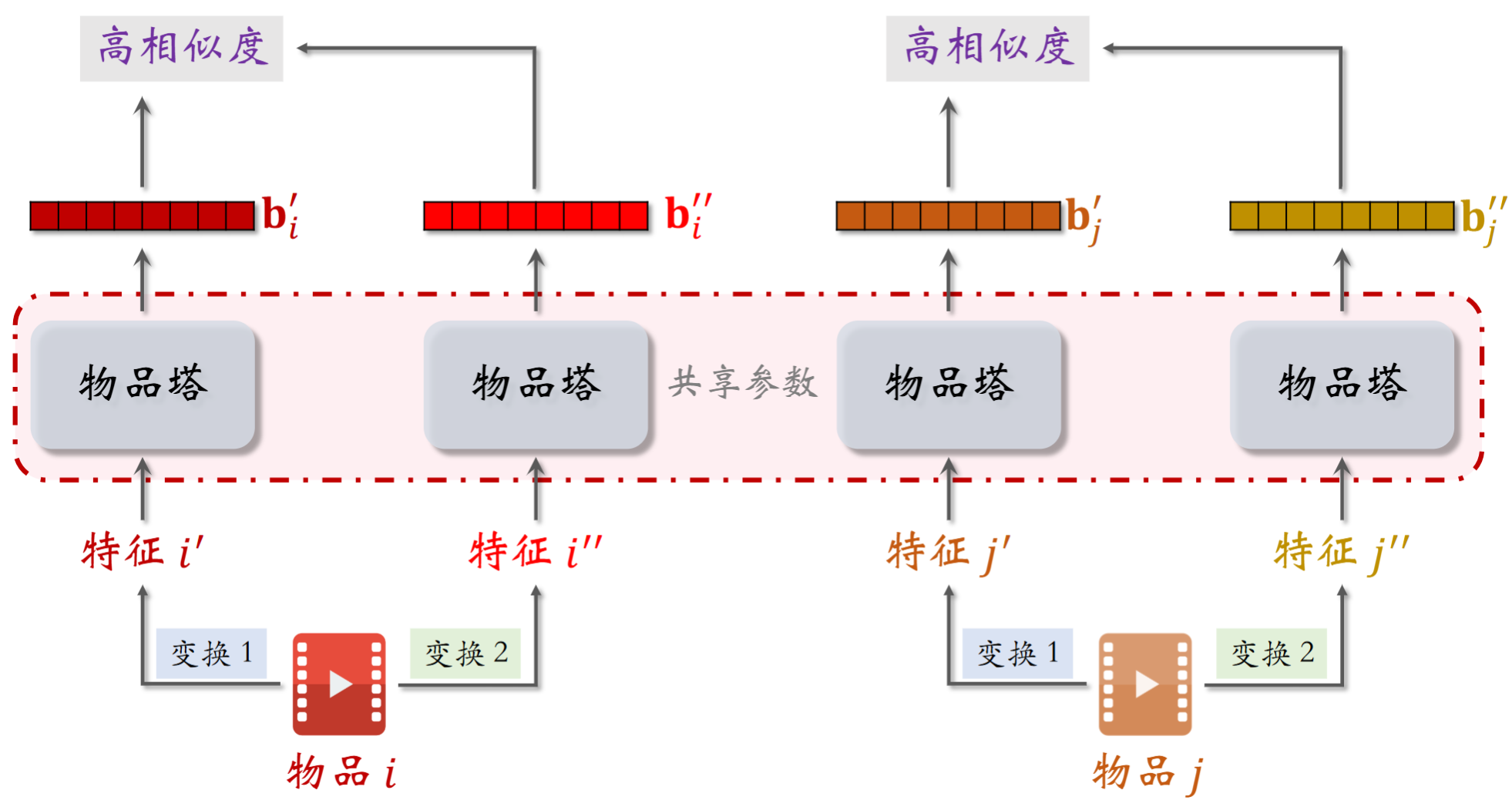
针对低曝光的物品的向量表征,通过自监督学习能够让长尾物品的曝光变得更准(只训练物品塔
针对物品 i,j,使用不同的(小幅度)特征变换,经过共享参数的物品塔(即参数实时更新同步)生成嵌入向量,同一物品生成的向量 \(b_{i}', b_{i}''\) 相似度应该是高的,而不同物品生成的向量 \(b_{i}', b_{j}'\) 相似度应该是低的。
特征变换
- random mask
- 随机选取离散特征进行掩码,设置为 default
- 相当于完全丢弃了某一特征所有属性
- dropout
- 随机选取多值离散特征,随机丢弃一部分
- complementary
- 将特征均匀分为两组,任意一组特征保留实际值,另一组特征使用 default 即可作为一种特征变换
- Associated mask
- 将一组“互相关联”的特征都掩码,关联度使用互信息 (mutual information) 来衡量
- 效果好,但是复杂、维护难
这么一来,如果我们对 n 个物品做两种特征变换得到 \(b', b''\),那么 \(b_{i}'\) 与 \(b_{i}''\) 取余弦相似度应该接近 1,\(b_{i}'\) 与 \(b_{j}'', j\neq i\) 的余弦相似度应该接近 0,这类似于前面提到的 batch 负样本,同样是使用 softmax + CrossEntropyLoss 进行训练。推导不难得到损失函数(由于物品热度不影响此处的抽样,不做纠偏
同样是对 batch 取平均 \(\frac1m\sum_{i=1}^mL_\text{self}[i]\)
训练损失 ¶
综合双塔模型训练和物品塔训练,随机选取 n 个用户 - 物品对作为一个 batch,对双塔模型进行训练;再随机选取 m 个物品作为一个 batch,对物品塔使用自监督学习进行训练
Product Neural Network (PNN)¶
FNN 将神经网络的高阶隐式交叉加到了 FM 的二阶特征交叉上,一定程度上说明了 DNN 做特征交叉的有效性。
PNN 虽然也用了 DNN 来对特征进行交叉组合,但是并不是直接将低阶特征放入 DNN 中,而是设计了 Product 层先对低阶特征进行充分的交叉组合之后再送入到 DNN 中去。
PNN 模型其实是对 IPNN 和 OPNN 的总称,两者分别对应的是不同的 Product 实现方法,前者采用的是 inner product,后者采用的是 outer product。
架构概览 ¶
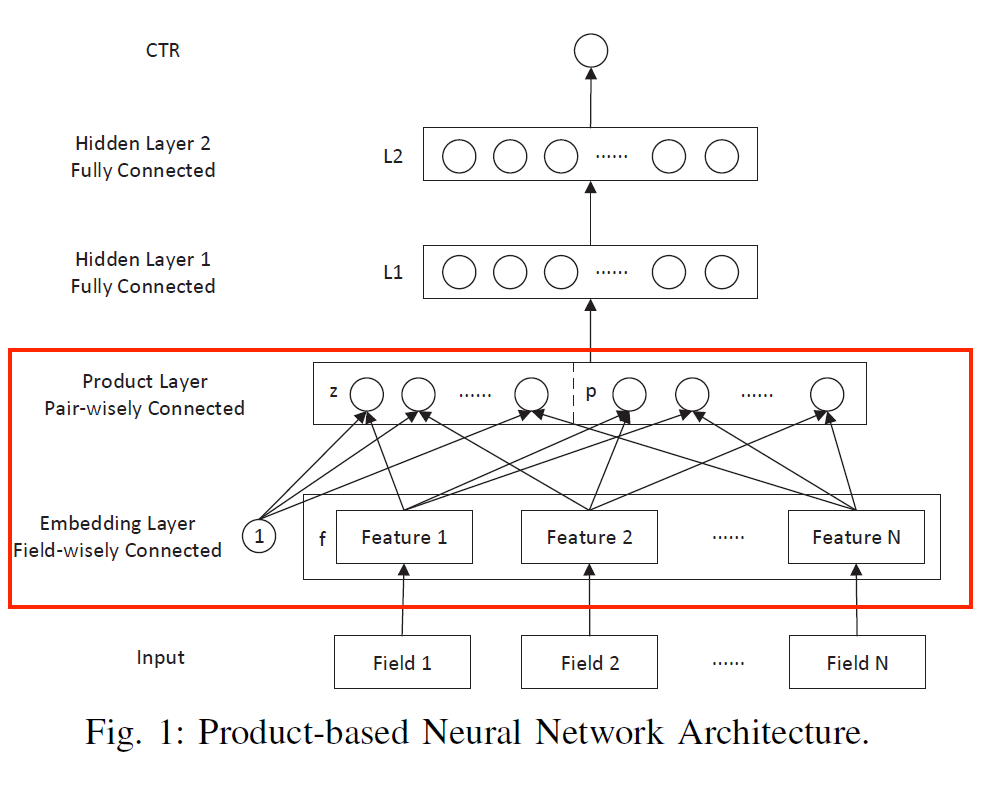
字段 (field)
在推荐系统中,特征通常会被组织成不同的字段(field
通常 field 是独热码(高维稀疏向量,下一步一般先嵌入为低维稠密向量
上图是 PNN 的架构概览图,我们特别关注 Product Layer,其余部分没有啥特点 ~(如果还看不懂得反思一下了)~。
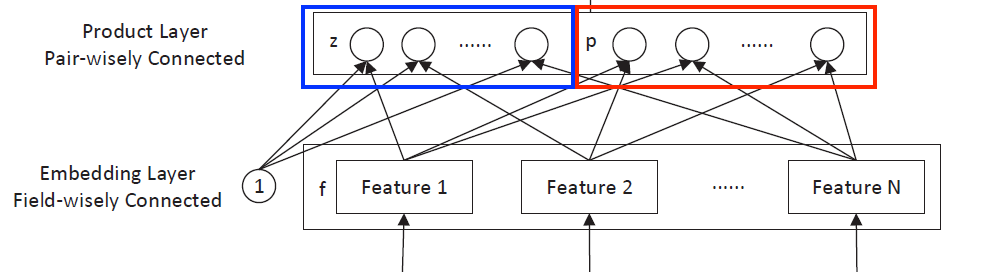
Product layer 由线性部分和非线性部分构成(\(f_{n} = W_{0}^{n}x[\mathrm{start_{n}: end_{n}}] \in \mathbb{R}^{M}, n \in [1..N]\) 1 表示特征向量,N 为特征数量,M 为嵌入维度
Tensor matrix inner product \(\odot\)
记符号 \(\odot\) 在矩阵间使用时为: \(A\odot B\triangleq\sum_{i,j}A_{i,j}B_{i,j}\)
线性模块 ¶
线性模块输入由一阶特征(未经过显示特征交叉处理)直接获取 \(\(z = (z_{1}, z_{2}, \dots, z_{N}) \triangleq (f_{1}, f_{2}, \dots, f_{N})\)\)
计算 \(\(l_{z}^{d} = W_{z}^{d} \odot z = \sum_{i =1}^{N}\sum_{j = 1}^{M}(W_{z}^{d})_{i,j} \cdot z_{i, j}, d \in [1..D_{1}]\)\) 得到 \(\(l_z=(l_z^1,l_z^2,...,l_z^{D_1}) \in \mathbb{R}^{D_{1}}\)\)
非线性模块 ¶
非线性模块输入由高阶特征(经过显示特征交叉处理) \(\(p = \{p_{i, j}\} \in \mathbb{R}^{N\times N}\)\) 计算 \(\(l_{p}^{d}=W_{p}^{d} \odot p = \sum_{i =1}^{N}\sum_{j = 1}^{M}(W_{z}^{d})_{i,j} \cdot p_{i, j}\)\) 得到 \(\(l_p=(l_p^1,l_p^2,...,l_p^{D_1}) \in \mathbb{R}^{D1}\)\)
求解 p ¶
第一个隐藏层的计算为:\(l_{1} = \mathrm{relu}(l_{z} + l_{p} + b_{1})\),剩下的任务在于如何计算 \(p_{i, j}\) 。在 IPNN 和 OPNN 中有所区别。
IPNN¶
IPNN 取 \(p_{i, j} = \left< f_{i}, f_{j} \right>\) ,即 \(l_{p}^{d}=\sum_{i =1}^{N}\sum_{j = 1}^{M}(W_{z}^{d})_{i,j} \cdot p_{i, j} = \sum_{i =1}^{N}\sum_{j = 1}^{M}(W_{z}^{d})_{i,j} \cdot \left< f_{i}, f_{j} \right>\);结合 FM 中的二阶交叉特征 操作有:
OPNN¶
OPNN 取 \(p_{i, j} = f_{i}f_{j}^{T}\) ,此时 \((W_{p}^{d})_{i, j}\) 应该是一个 \(N\times N\) 的矩阵,并改为矩阵内积:
论文中也有优化而稍微修改了计算方式,这里按下不表。
DCN¶
在前面我们提到了很多“神经网络”,具体实现有非常多种,往往结合不同类型“层”堆叠成“网”。下面讨论 Deep&Cross Network (DCN) 。
交叉层 ¶
在 DCN 中需要使用交叉层。
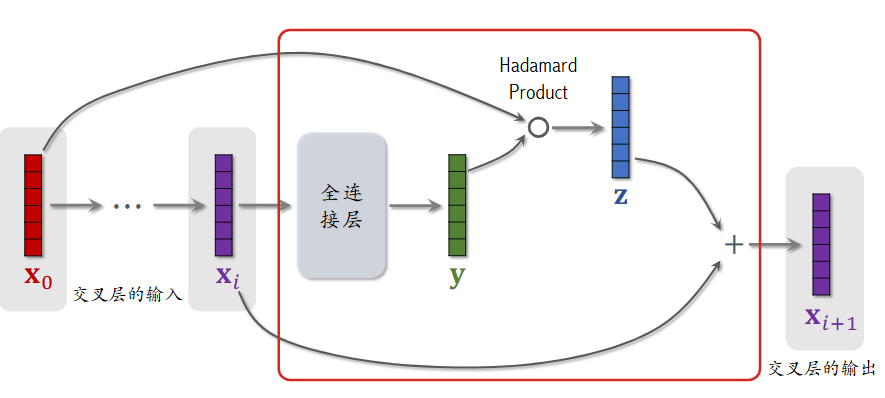
上图中红色方框内部分为一个交叉层:对于输入 \(x_{i}\),经过全连接层后得到 y,与最初的输入执行 Hadamard 乘积(逐元素相乘,运算后维度保持不变,之后使用 \(\odot\) 表示)得到 z,最后与 \(x_{i}\) 相加得到 \(x_{i+1}\),公式表示为:
交叉网络 ¶
将上述交叉层堆叠形成交叉网络:
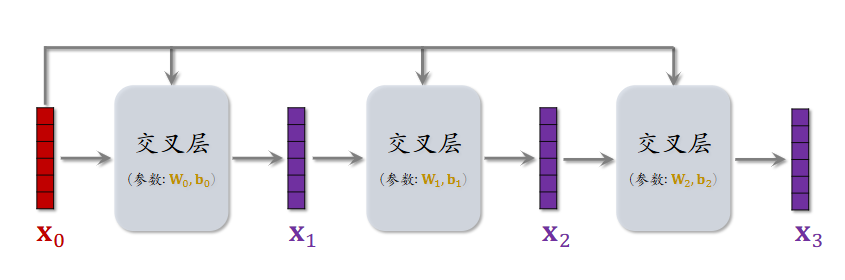
将交叉网络与全连接层相结合,共同构成深度交叉网络 (DCN),可以在召回和排序模型中使用。
LHUC¶
LHUC(Learning Hidden Unit Contributions) 起源于语音识别领域,快手将其应用于推荐系统精排中,称为 PPNet。
语音识别中的 LHUC ¶
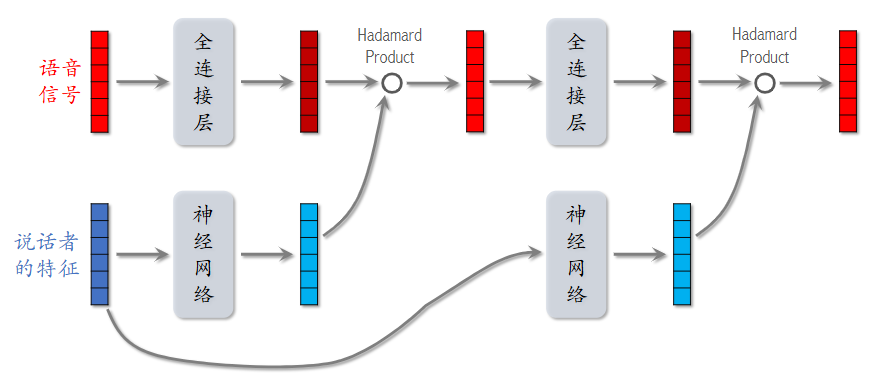
对于收到的语音信号和已有的说话者特征进行处理后进行 Hadamard 乘积得到输出,多层重复可以得到最终的输出。其中神经网络一般由多个全连接层构成,最后使用 sigmoid 的两倍来将输出向量的每个元素控制在 \((0, 2)\) 范围内,用于对语音信号进行对应的放缩(两倍是经验性的一个抉择
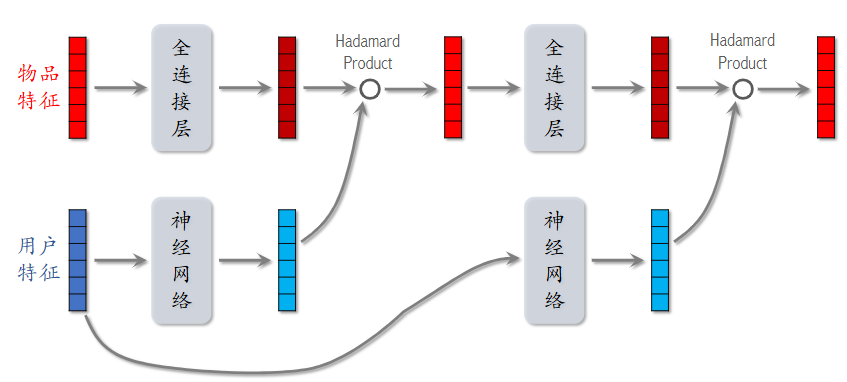
推荐系统中的 LHUC ¶
推荐系统中网络结构基本一致,对应使用物品特征和用户特征即可,用于精排阶段。
FiBiNet¶
FiBiNet 将 SENet 和 Bilinear Cross 进行了结合:
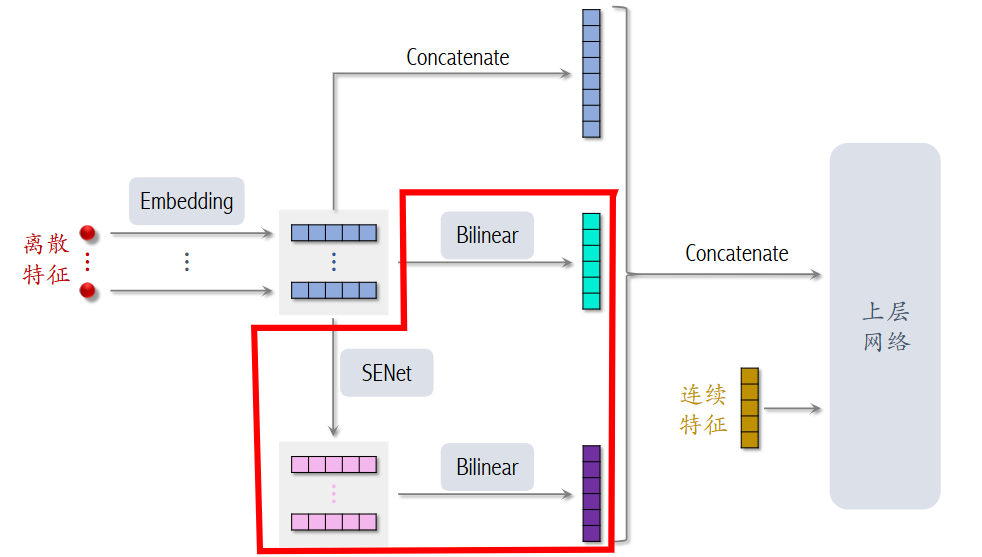
SENet¶
SENet 是 Squeeze-and-Excitation Networks 的缩写,是一种自适应特征提取的注意力机制。给定 m 个离散特征,将其嵌入为向量(嵌入维度可以各不相同,出于简单暂时记为 k 维
- Squeeze: 针对每个特征做 AvgPool,即对特征向量元素求平均,得到 mx1 向量
- Excitation: 经过 FC+ReLU 、FC+Sigmoid 得到新的 mx1 向量,这个向量表征了特征的重要性
- Re-weight: 使用新向量对离散特征的嵌入向量做乘积得到新的整体嵌入向量
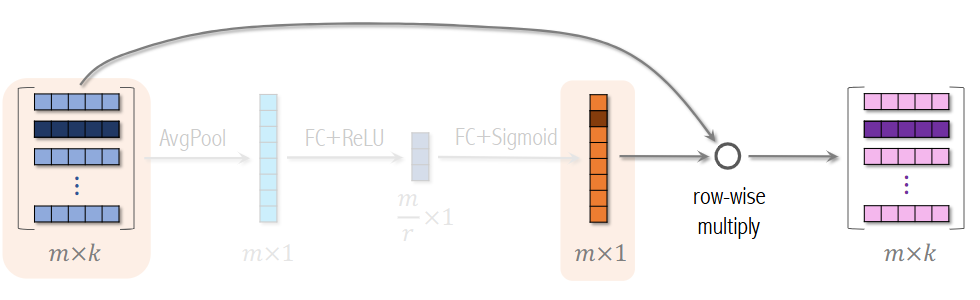
不严谨地说,这里表征特征的嵌入向量即为一个 Field,SENet 即是对离散特征做 field-wise 加权;这有利于将大量低频无用的特征进行抛弃,强化高频有效特征的作用。
Bilinear Cross¶
目前我们使用的特征交叉方式有(都要求 field 的长度一致
- 内积 (Inner Product)(余弦相似度本质没啥区别,只是归一化了)
- 从 m 个 field 中可以得到 \(\frac{m^{2}}{2}\) 个实数
- Hadamard Product
- 从 m 个 field 中可以得到 \(\frac{m^{2}}{2}\) 个 k 维向量
Bilinear Cross 能够支持不同长度的特征做做特征交叉,核心在于在中间添加一个参数矩阵。基于乘积方法分为内积版本和哈达玛乘积版本。
Inner Product¶
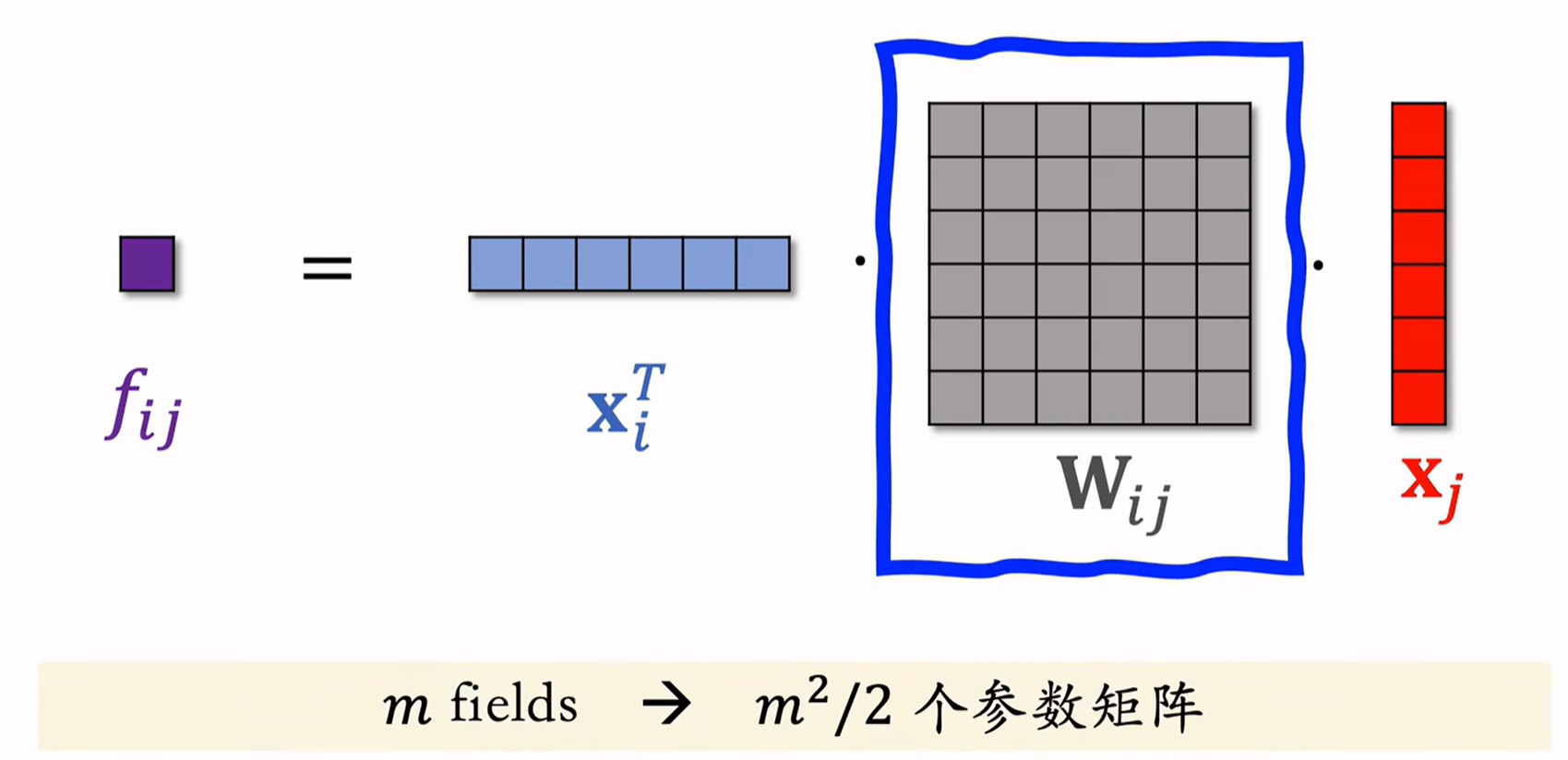
如上图所示,特征交叉最后得到 \(f_{ij} = x_{i}^{T} \cdot W_{ij} \cdot x_{j}\) ;由于参数矩阵有可能较大,一般不会对所有特征做交叉,人工选取重要特征再来做交叉。
Hadamard Product¶
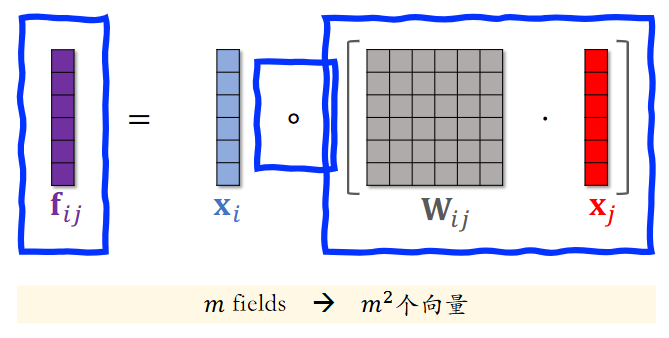
将第一个符号改为哈达玛乘积,可得到 \(\frac{m^{2}}{2}\) 个向量。