排序 ¶
多目标排序 ¶
在对物品召回后,我们需要对召回物品进行排序以筛选出合适数量的推荐内容。由于一般需要考虑的指标非常多,包括点击率、点赞率、收藏率、转发率等,为了综合考虑这些指标融合评估,我们一般训练使用多目标模型进行融合(例如加权和,更多可见 bilibili / rank-03
点击率、点赞率、收藏率、转发率
- 点击率 = # 点击 / # 曝光
- 点赞率 = # 点赞 / # 点击
- 收藏率 = # 收藏 / # 点击
- 转发率 = # 转发 / # 点击
多目标预估 ¶
首先对可考虑特征(用户特征、物品特征、统计特征、场景特征,更多可见 bilibili / rank-05)嵌入成为向量,拼接后输出神经网络得到综合嵌入向量(显然这属于前期融合,而双塔模型属于后期融合
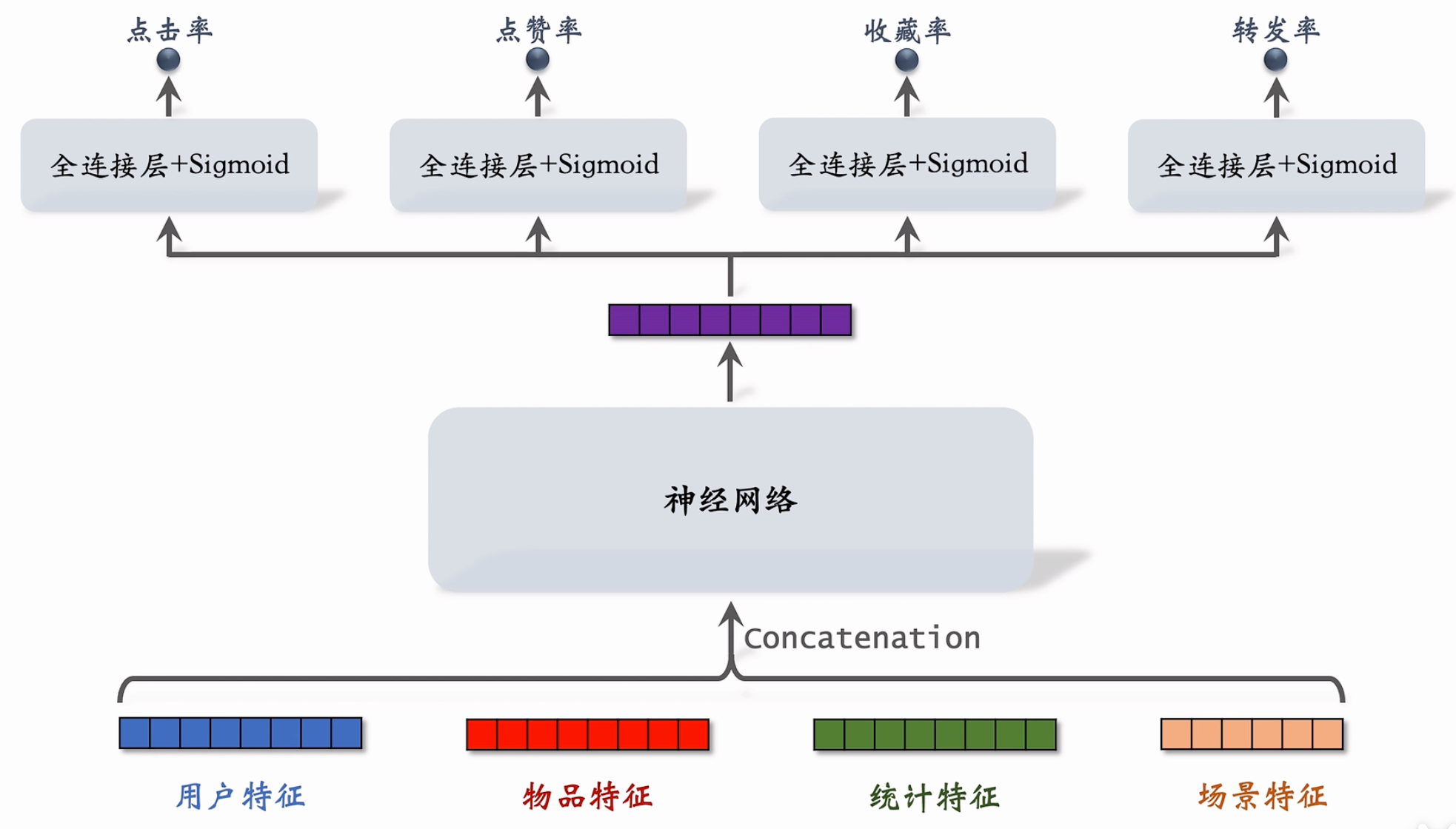
样本不均衡 ¶
以我们自己的使用经历为例,对于系统推荐的内容,实际被点击的物品数量相对于所有曝光的物品数量的比例是较低的,点赞、收藏、转发比例在点击率低的前提下更低,这导致在这些方面的训练时正负样本严重不平衡导致训练效果变化不显著而成本增高。
负样本降采样 ¶
为此,我们一般使用负样本降采样 (down-sampling) 的策略,即从负样本中随机抽取一部分(采样率为 \(\alpha \in (0, 1)\))保留,其余舍弃以节约计算。
预估值校准 ¶
但是这样出现了一个问题,如果我们原本将未被点击的物品作为负样本,那么采样后负样本减少,计算得到的预估点击率将会偏高。因为真实点击率和预估点击率分别为:
消去样本可以得到
MMoE¶
MMoE 是 Multi-gate Mixture-of-Experts 的缩写,即多门混合专家模型;具体而言,一个神经网络可能不能够较好地捕捉多个目标需求,多个“专家”(即多个神经网络)能够关注不同的角度以较为全面的从特征信息中做出预估。
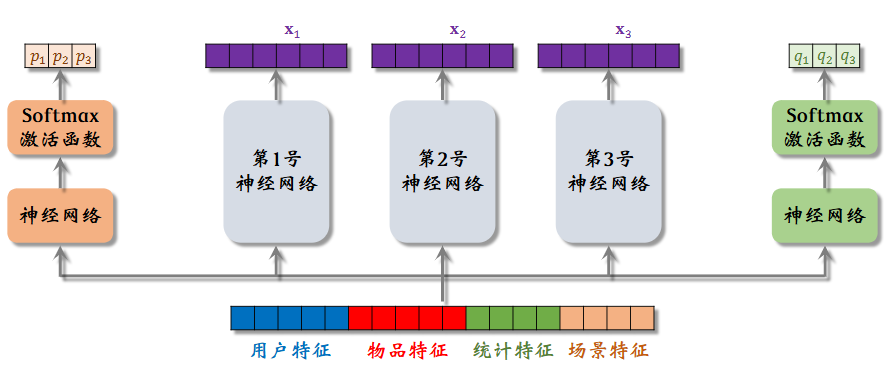
如上所示,图中的第 1/2/3 号神经网络即为“专家”(实际业务中会使用更多,假设为 e 个
e 维度向量将要作为权重对 e 个专家的输出向量进行加权求和,得到混合的特征向量,交给下一个神经网络进行对应目标的预估。
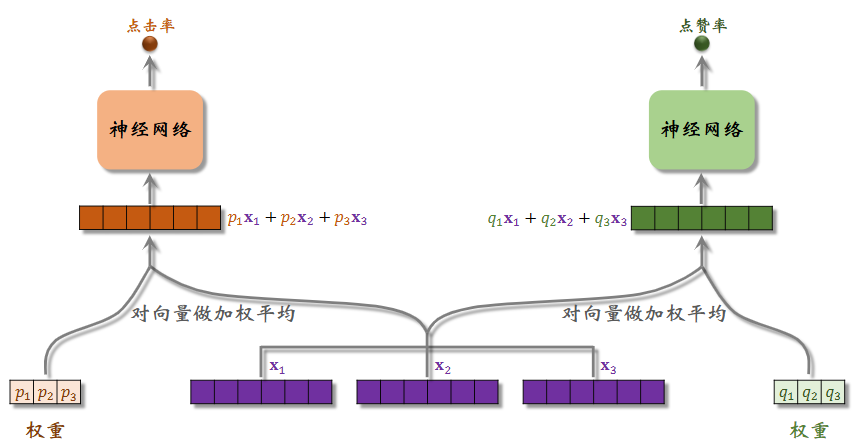
极化现象(Polarization)
极化 (polarize):Softmax 输出值一个接近 1,其余接近 0。
换言之,某一个专家的“声音”太大了,模型退化为简单的预估模型
解决方案: Dropout;具体而言,在训练时,对于 softmax 输出的权重向量有 \(\beta\) 概率被 mask,也即每个专家有 \(\beta\) 概率被丢弃;此时如果极化现象严重,那么一但对应专家被丢弃效果将非常差并反馈,作为一种罚项。
视频排序 ¶
对于图文笔记,点击、点赞、收藏、转发等指标是最为重要的,而如果物品是视频,播放时长和是否完播变得更为关键。
播放时长 ¶
播放时长作为连续变量,直接使用回归预估却效果较差。
Deep Neural Networks for YouTube Recommendations 中使用全连接层建模:
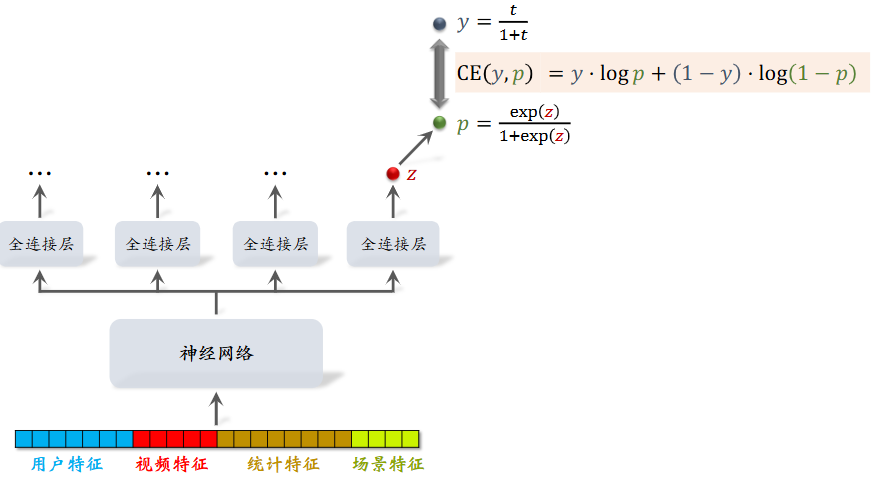
在上图中,对于全连接层输出的 logit \(z \in (- \infty, + \infty)\) 进行 sigmoid,即 \(p = \sigma(z) = \frac{1}{1+ e^{-z}}= \frac{e^{z}}{1+ e^{z}} \in (0, 1]\),同时实际观看时长 \(t \in (0, +\infty)\),为了可以计算交叉熵损失同样压缩为 \(y = \frac{t}{1+t} \in (0, 1)\) 。
不难发现,当我们期望 \(p \approx y \implies \exp (z) \approx t\) ,即用训练好的模型的输出 z 的 \(\exp(z)\) 作为预估时长,同样可以作为融分公式的一项
视频完播 ¶
在实际业务中,视频真正完全播放完毕的样本是较为稀疏的,不利于模型训练;往往依据实际效果对“视频完播”予以新的定义。
例如,有时我们认为视频播放了 80% 以上已经能够说明用户对该视频较为感兴趣,那么可以将 80% 作为完播指标;播放时长高于视频总时长 80% 的视频我们都认为完播,否则认为未完播 。那么训练出的模型即为一个二元分类模型,预估视频被观看超过 80% 的概率。
又或者我们可以让模型直接预估视频将被观看的时长比例 ,训练时同样使用交叉熵损失。
结合实际经验和数据来看,短视频比长视频的完播率较高,完播率与视频时长大致呈反比例关系。直接使用上面得到的预估完播率作为融分公式中一项将对短视频有利。
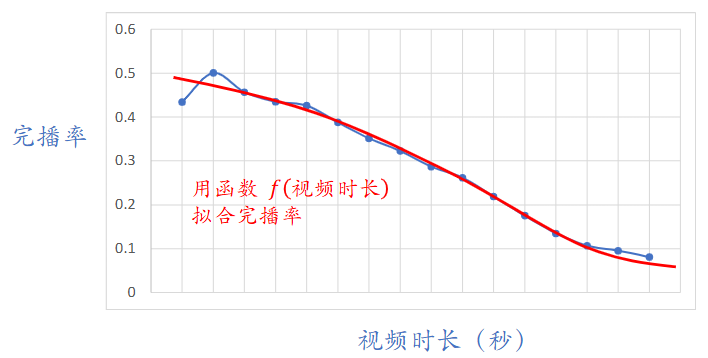
只考虑视频时长与完播率的关系,我们使用 f 进行拟合,并对视频完播分数进行修正(修正后可以作为融分公式的一项
粗排(三塔模型)¶
在多目标排序一节中我们介绍的模型主要用于精排,其前期融合导致可存储、复用的内容较少,每次都需要经过完整的模型推理得到结果。
粗排位于召回和精排之间,其精确度应该高于召回而快于精排。我们先回顾一下召回和精排。
召回 ¶
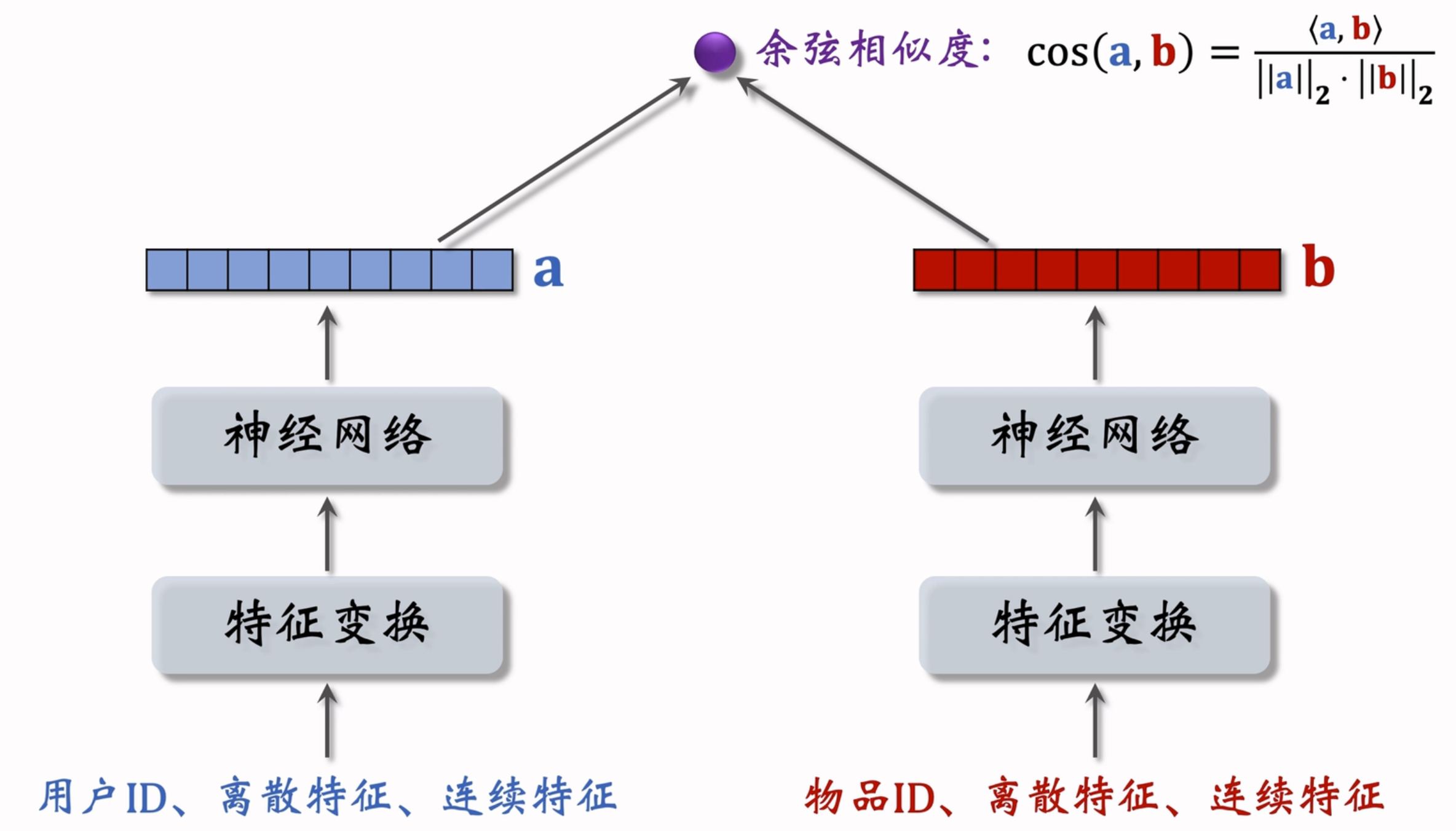
回顾双塔模型,两个塔对用户和物品的特征分别输入神经网络做变换,在最后输出特征向量后做余弦相似度计算。用户和物品的特征向量可以保留重复使用,因而实际塔内推理较少,效率较高。
精排 ¶

正如开始所言,精排模型将特征在最开始即进行了融合,这要求我们针对每一对用户 - 物品都需要重新进行推理,因而实际花费时间较长,但实际发现最后效果也更好。
粗排 ¶
基于效率和质量的妥协,阿里提出了三塔模型:
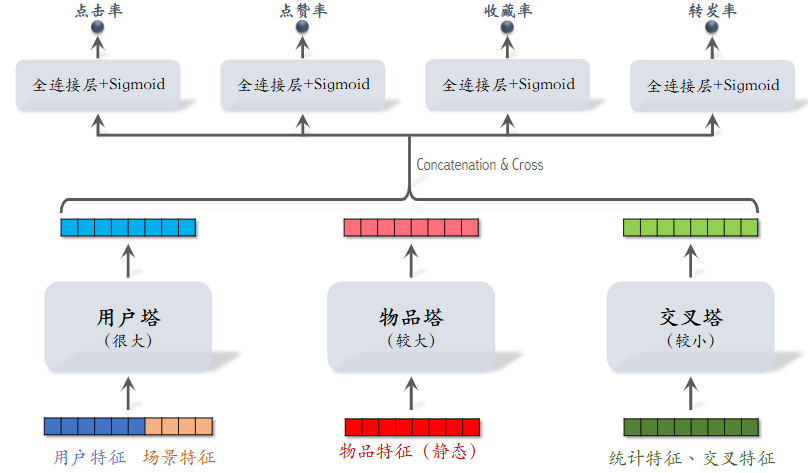
除去用户塔和物品塔外,添加一个交叉塔以针对统计特征、交叉特征(等更新快、时效性高的特征)进行拟合变换,拼接融合后输入全连接层用于之后的任务。可以看到三塔模型在中期融合,对用户和物品本身更新慢的特征进行复用,同时对于更新较快的特征使用简单的模型以提高速度。
考虑一个用户的实际请求,我们已经从召回阶段获取了 n 个物品:
- 用户塔:1 次推理,即发送请求的用户本身
- 物品塔:借用缓存,往往只有 \(\frac{n}{100}\) 的物品需要推理
- 交叉塔:n 次推理,但是非常快
- 全连接层:n 次推理,每次都必须调用
-
全连接层是一个 / 一组简单的线性加权,详细可见 3.1. 线性回归 — 动手学深度学习 ↩